cache测试及其矩阵优化

利用c/c++测试电脑的cache参数，知识点主要有以下几个：

1. SSE 指令预取

Intel公司的单指令多数据流式扩展（SSE，Streaming SIMD Extensions）技术能够有效增强CPU浮点运算的能力。具体情况请移步维基。

C++中包含SSE指令的头文件：
#include

预取指令：_mm_prefetch
void _mm_prefetch(char *p, int i)
从地址P处预取尺寸为cache line大小的数据缓存，参数i指示预取方式（_MM_HINT_T0, _MM_HINT_T1, _MM_HINT_T2, _MM_HINT_NTA，分别表示不同的预取方式）
T0 预取数据到所有级别的缓存，包括L0。
T1 预取数据到除L0外所有级别的缓存。
T2 预取数据到除L0和L1外所有级别的缓存。
NTA  预取数据到非临时缓冲结构中，可以最小化对缓存的污染。
如果在CPU操作数据之前，我们就已经将数据主动加载到缓存中，那么就减少了由于缓存不命中，需要从内存取数的情况，这样就可以加速操作，获得性能上提升。使用主动缓存技术来优化内存拷贝。

注意，CPU对数据操作拥有绝对自由！使用预取指令只是按我们自己的想法对CPU的数据操作进行补充，有可能CPU当前并不需要我们加载到缓存的数据，这样，我们的预取指令可能会带来相反的结果，比如对于多任务系统，有可能我们冲掉了有用的缓存。不过，在多任务系统上，由于线程或进程的切换所花费的时间相对于预取操作来说太长了, 所以可以忽略线程或进程切换对缓存预取的影响。

参考：MSDN
http://hi.baidu.com/sige_online/blog/item/a80522ceec812433b700c829.html
http://www.codeguru.com/forum/archive/index.php/t-337156.html
http://blog.csdn.net/igame/archive/2007/08/21/1752430.aspx


2. 编译带有SSE指令的程序
需要使用以下选项：
g++ -Wall -march=pentium4 -mmmx -o run.out test.cpp

否则就会出现如下类似错误：
/usr/lib/gcc/i386-redhat-linux/4.1.2/include/xmmintrin.h:34:3: error: #error "SSE instruction set not enabled"

如果是多线程程序，还要加上-lpthread选项


3. 计时函数

3.1 clock()

#include

获得该程序从启动到函数此处调用占用CPU的时间
常量CLOCKS_PER_SEC，它用来表示一秒钟会有多少个时钟计时单元
可以使用公式clock()/CLOCKS_PER_SEC来计算一个进程自身的运行时间，单位为秒

3.2 gettimeofday()

#include
int gettimeofday(struct timeval*tv, struct timezone *tz)
gettimeofday()会把目前的时间用tv结构体返回，当地时区的信息则放到tz所指的结构中

struct  timeval{
    long  tv_sec;/*秒*/
    long  tv_usec;/*微妙*/
};

struct  timezone{
    int tz_minuteswest;/*和greenwich 时间差了多少分钟*/
    int tz_dsttime;/*type of DST correction*/
};

在gettimeofday()函数中tv或者tz都可以为空。如果为空则就不返回其对应的结构体。
函数执行成功后返回0，失败后返回-1，错误代码存于errno中。
在使用gettimeofday()函数时，第二个参数一般都为空，因为我们一般都只是为了获得当前时间，而不用获得timezone的数值

4. 矩阵优化

大矩阵的计算时间主要消费在IO访问上，可以利用cache的空间局部性原理，对矩阵的IO进行优化，本文主要是从行列相乘入手，利用转置和分块法进行优化

5. 预取数据程序

/*
 * auth = peic
 * 预取数据
 */
#include 
#include 
#include 
#include 
#define N 1024 * 1024 * 256
#define PREFETCH 2

using namespace std;

 int main()
 {
	int* x = new int[N];
 	int* y = new int[N];
 	int i, sum = 0;
 	double start_time = 0, end_time = 0;
 	start_time = (double)clock() / CLOCKS_PER_SEC;
 	for(i = 0; i < N; i+=(PREFETCH/2))
 	{
 		sum += (*(x+i)) * (*(y+i));
 	}
 	end_time = (double)clock() / CLOCKS_PER_SEC;
 	cout << "without prefetch, time = " << (end_time - start_time) << "s" << endl;

 	start_time = (double)clock() / CLOCKS_PER_SEC;
 	for(i = 0; i < N-PREFETCH; i+=(PREFETCH/2))
	{


 		_mm_prefetch(x+PREFETCH, _MM_HINT_T0);
 		_mm_prefetch(y+PREFETCH, _MM_HINT_T0);
 		sum += (*(x+i)) * (*(y+i));
	}
	end_time = (double)clock() / CLOCKS_PER_SEC;
 	cout << "* with prefetch, time = " << (end_time - start_time) << "s" << endl;

 	//system("pause");
	return 0;
 }

程序运行结果：

6. cache大小测试程序及其结果

cache行大小测试

/*
 * auth = peic
 * 测试cache行的大小
*/

#include 
#include 
#include 
#include 

#define KB (1024)
#define MB (1024 * 1024)
#define SIZE (64 * MB)
using namespace std;

//定义获取微秒时间的函数
double getTime()
{
	struct timeval tv;
	gettimeofday(&tv, NULL);
	//获取秒
	double sec = (double)tv.tv_sec;
	//获取微秒
	double usec = (double)tv.tv_usec;
	//返回微秒数
	return sec * 1000000 + usec;
}


//定义遍历数组函数
int traverse(int* array, int len, int interval)
{
	for(int i = 0; i < len; i += interval)
	{
		*(array+i) *= 10;
	}
	return 1;
}

int main()
{
	int *array = (int *)malloc(SIZE * sizeof(int));
	double begin_time;
	double end_time;
	//数组初始化
	for(int i = 0; i < SIZE; i++)
	{
		*(array+i) = i;
	}

	//使用不同步长遍历数组，输出程序执行时间
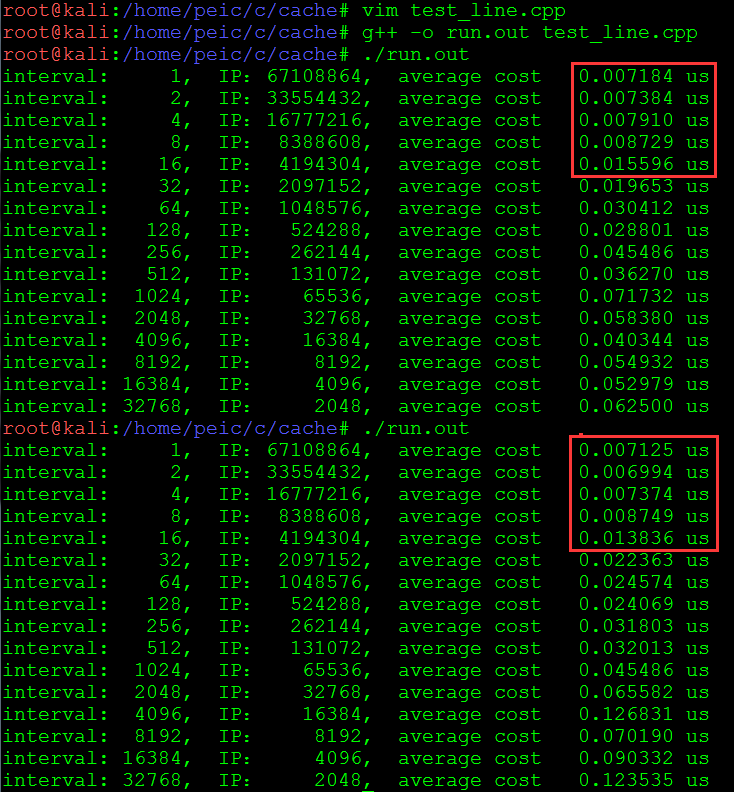
	for(int interval = 1; interval < 64 * KB; interval *= 2)
	{
		begin_time = getTime();
		traverse(array, SIZE, interval);
		end_time = getTime();
		//删除步长，指令数，每条指令的花费
		printf("interval: %5d,  IP：%8d,  average cost %10lf us\n", interval, SIZE/interval, (end_time - begin_time) / (SIZE/interval));
	
	
	}
	return 1;
}

程序运行结果（时间发生明显跳变就是cache断行，据此推测cache的行大小，块测试同理）：

cache块大小测试

/*
 * auth = peic
 * 测试不同级cache的大小
 */
#include 
#include 
#include 
#include 

#define KB (1024)
#define MB (1024 * 1024)
#define SIZE (64 * MB)
using namespace std;

//定义获取微秒时间的函数
double getTime()
{
	struct timeval tv;
	gettimeofday(&tv, NULL);
	//获取秒
	double sec = (double)tv.tv_sec;
	//获取微秒
	double usec = (double)tv.tv_usec;
	//返回微秒数
	return sec * 1000000 + usec;
}


//定义遍历数组函数
//size为设定的cache块大小
int traverse(int* array, int size)
{
	//获得size的二进制的后几位
	int len = size - 1;

	for(int i = 0; i < SIZE; i++)
	{
		//cache行的大为16
		array[(i*16) & (len)] *= 3;
	}
	return 1;
}

int main()
{
	int *array = (int *)malloc(SIZE * sizeof(int));
	double begin_time;
	double end_time;
	//数组初始化
	for(int i = 0; i < SIZE; i++)
	{
		*(array+i) = i;
	}

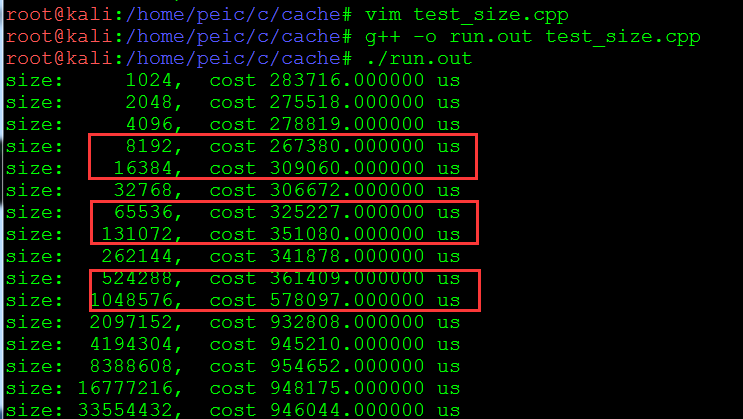
	for(int size = 1024; size < SIZE; size *= 2)
	{
		/*
		if(size == 2*MB/sizeof(int))
		{
			size = 3*MB / sizeof(int);
		}
		*/
		begin_time = getTime();
		traverse(array, size);
		end_time = getTime();
		//输出不同cache块的花费
		printf("size: %8d,  cost %10lf us\n", size, (end_time - begin_time));
	
	}
	return 1;
}

程序运行结果（3级cache，3级跳变）：

7. 矩阵运算优化

普通运算：

/*
 * auth = peic
 * 直接进行矩阵乘法运算，未做任何优化
*/

#include 
#include 
#include 

#define N 1024

void MartixMultip(int* A, int* B, int* C, int size)
{
	int i, j, k;
	for(i=0; i < size; i++)
	{	
		for(j=0; j

转置后再计算

/*
 * auth = peic
 * 对矩阵乘法进行优化， 对矩阵进行转置
 */

#include 
#include 
#include 

#define N 1024

void MartixMultip(int* A, int* B, int* C, int size)
{
	int i, j, k;
	//先对矩阵进行转置
	int *tmp = (int *)malloc(sizeof(int) * size * size);
	for(i=0; i

分块运算

/*
 * auth = peic
 * 矩阵乘法优化，对矩阵进行分块
 */

#include 
#include 
#include 

#define N 1024
int min(int a, int b)
{
	return a < b ? a : b;
}
void MartixMultip(int* A, int* B, int* C, int size, int block)
{
	int i, j, k;
	//先循环分块
	for(int ii=0; ii < size; ii += block)
	{	
		for(int jj=0; jj

运算结果：

从结果上看，转置的优化很明显。分块依赖于矩阵的规模和分块规模的选择，因为分块带来中间的消耗，需要寻找最佳的分块方案。

举这些例子只是想表明，有时候，很简单的一些方法就能极大的提高程序的运行效率。