图卷积网络GCN理解
图卷积网络(Graph Convolutional Network,GCN)是近年来逐渐流行的一种神经网络结构。不同于只能用于网格结构(grid-based)数据的传统网络模型 LSTM 和 CNN,图卷积网络能够处理具有广义拓扑图结构的数据,并深入发掘其特征和规律,例如 PageRank 引用网络、社交网络、通信网络、蛋白质分子结构等一系列具有空间拓扑图结构的不规则数据。相比于一般的拓扑图而言,人体骨骼拓扑图具有更加良好的稳定性和不变性,因此从2018年开始,就有许多学者尝试将图卷积网络应用到基于人体骨骼的行为识别领域来,也取得了不错的成果。下面就让我们来深入了解一下什么是图卷积网络,以及它在行为识别领域的最新工作进展吧!
什么是图(graph)?为什么要研究GCN?
我们知道,CNN 在处理图像数据时具有很强的特征抽取能力和整合能力,这得益于卷积核(kernel ,or filter)的参数共享机制和加权平均机制。卷积本质上就是一种加权求和的过程,而卷积核的参数就是不同像素点对应的权重,并且不同的图片都共享同一个卷积核,这使得CNN能够通过对卷积核参数的迭代更新来隐式的学习图像中具有的像素排列规律,进而学习到不同的形状特征和空间特征。
但值得注意的一点是,CNN 所处理的数据都具有规则的网格结构,也就是排列很整齐的矩阵,具有 Euclidean Structure,例如 RGB 图片(图1)。如果要将CNN应用于非图像领域,就必须将数据组合为规整的网络结构,才能作为CNN的输入。例如在 18 年之前的行为识别研究中,常用的方法就是以一定的顺序将一个动作的关节坐标序列转换为一张 RGB 图片,从而将动作识别工作转化为图像识别工作。
图1 规则空间结构数据
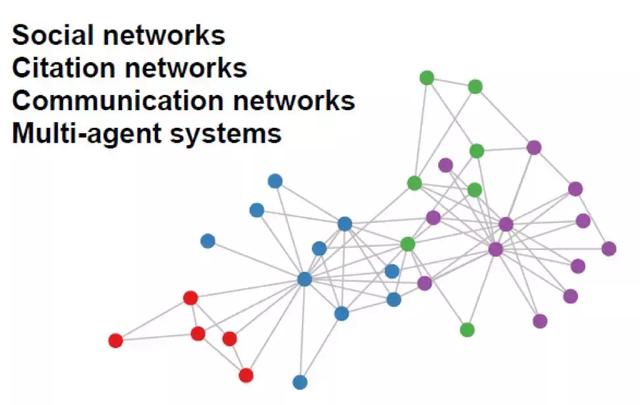
然而现实生活和科学研究中有很多数据都不具备完整的矩阵结构,相反,更多的是以一定的连接关系聚合在一起,如图2所示。社交网络,通信网络,互联网络等都具有类似的结构。
图2 社交网络拓扑图
类似这样的网络结构就是图论中所定义的拓扑图。更一般的,图就是指图论中用顶点和边建立相应关系的拓扑图。我们可以用一个点和边的集合来表示图:G=(E,V);其中E表示边的集合,V表示顶点的集合。
那么对于这种具有拓扑图结构的数据而言,CNN 处理起来是非常困难的(但也不是没有办法哦),而且通常不能很好的抽取节点与节点之间的连接关系信息(是否相连),这也是我们研究 GCN 的重要原因。当然,根本的原因还是在于数据的多样性,广义上来讲,任何数据在赋范空间内都可以建立拓扑关联,谱聚类就是应用了这样的思想。所以说拓扑连接是一种广义的数据结构,GCN 有很大的应用空间。
图卷积操作如何进行呢?
目前有两种类型的图卷积操作,一种是基于空域的图卷积,另一种是基于谱域的图卷积,这里着重介绍第一种。
前面我们提到,卷积操作的本质意义就是对一个范围内的像素点进行加权求平均,这能有助于提取空间特征,那么如何将这种思想应用到拓扑图上呢?我们可以换一种方式来理解卷积操作,如图3,对于feature map(蓝色部分)中的一个点(红色),其特征值实际上是周围所有像素点将特征值传播到中心点后进行加权平均,这种操作等效于传统的卷积操作,只不过我们人为的为特征添加了一个传播方向(边),将每个像素点当成顶点,从而在图结构上再次定义了卷积操作。
图3 卷积操作的另一种理解
进一步的,对于广义拓扑图结构的数据,也可以按照这种思想来定义卷积操作,如图4所示,将每个节点的邻居节点的特征传播到该节点,再进行加权平均,就可以得到该点的聚合特征值,只不过在 CNN 中,我们将这个聚合特征值当做了 feature map 中的一个点,而在 GCN 中没有 feature map 的概念,我们直接将这个聚合特征值作为传播到下一层的特征值。蓝色部分就是图卷积操作对应的 kernel,这里是为了理解才画出这个蓝色区域,在 GCN 中也没有 kernel 的概念,这也是因为图是不规则的。
类似于 CNN,图卷积也采用共享权重,不过不同于 CNN 中每个 kernel 的权重都是规则的矩阵,按照对应位置分配,图卷积中的权重通常是一个集合。在对一个节点计算聚合特征值时,按一定规律将参与聚合的所有点分配为多个不同的子集,同一个子集内的节点采用相同的权重,从而实现权重共享。例如对于图4,我们可以规定和红色点距离为 1 的点为 1 邻域子集,距离为 2 的点为 2 邻域子集。当然,也可以采用更加复杂的策略,例如按照距离图重心的远近来分配权重。权重的分配策略有时也称为 label 策略,对邻接节点分配 label,label 相同节点的共享一个权重。
到这里想必你已经发现了,其实图卷积操作就是传统的卷积操作在拓扑图上的概念延伸和转移,通过对比二者,你能更好的学习到图卷积网络的精髓。
图4 拓扑图上的卷积操作
特征在层与层之间的传播方式可以用公式表示如下:
其中 Hi 是第 i 层的特征矩阵,当 i=0时,H0 就表示输入图的节点特征矩阵。A是输入图的邻接矩阵,Wi表示第i层的权重矩阵。σ表示激活函数。通过邻接矩阵左乘特征矩阵,可以实现特征的聚合操作,然后再右乘权重矩阵,可以实现加权操作。权重矩阵W和邻接矩阵H是用图卷积做行为识别工作时的重点研究对象。邻接矩阵的示例如下图:
图5 邻接矩阵示例
如果两个节点相邻,那么在矩阵中对应位置为1,否则为0。这是一种非常基础的定义,不同的行为识别工作会在此基础上设计不同的变体定义。
概括的来说,图卷积操作就是将每个节点的特征与其邻居节点的特征加权平均后传播到下一层。这种图卷积操作称为在空域上的图卷积,有如下几个特点:
1. 随着层数的加深,每个节点能聚合到的特征越远,也就是感受野越大。
2. 权重是共享的,不会具体到每个节点,这和传统CNN相同。(直观的理解,如果权重是因节点而不同的,那么一旦图结构发生变化,权重就会立刻失效)
3.每个顶点的邻居节点数可能不同,这导致邻居节点多的顶点的特征值更显著。
4.邻接矩阵在计算时无法将节点自身的特征包含到聚合特征值中。
此外,为了克服空域图卷积的缺点,学者们提出了谱域上的图卷积,大概思想是利用图的拉普拉斯矩阵和傅里叶变换来进行卷积操作。基于谱域的图卷积目前在行为识别中应用较少,并且原理非常复杂,这里不做详细介绍,有兴趣的同学可以阅读相关文章。
其他: