整合：图论存图方法及三种重要做法分析（Kruskal Dijkstra Bellman-Ford)

一、最短生成路的2种存图方法（邻接矩阵和邻接表）：

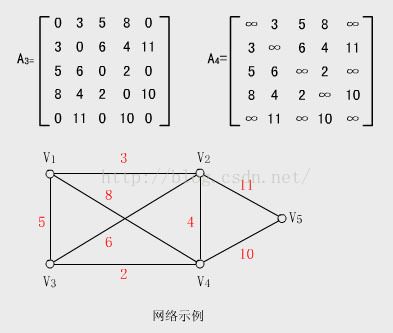
1）邻接矩阵（适合稠密图即边远远多于点）：

1、时间复杂度一般在n^2；
2、可以解决重边情况；map[i][j] = min( map[i][j] , input);
3、初始化；a[i][j] = INF;  a[i][i] = 0;
4、邻接矩阵点的最大极限在3000左右  
5、图示：

2）邻接表（适合疏密图即边数近似于点数）：

1、时间复杂度一般在mlog(n)；

2、数组实现邻接表：

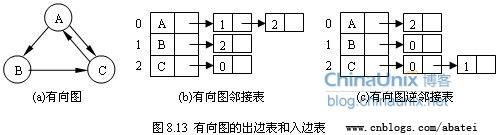
①定义：每个节点i都有一个链表，里面保存着从i出发的所有边。对于无向图来说，每条边会再邻接表中出现两次。

②方法：首先给每条边编号，然后用adj[u]来记录边的最后出现位置（初始化为-1），结构体中用next来表示上一条边出现的位置。下面的函数读入有向图的边列表，并建立邻接表：

③图示：

④代码：（以poj 3159为例 简单数组 + 栈 模拟）

#include 
#include 
#include 
#include 
#include 
#include 
#define MAXN 150005
const int INF = 9999999;
using namespace std;
int N, M;
struct node{
    int to, cost;
    int next;
};
node e[150005];
//e数组读取边的信息
int d[30005], adj[30005];
//d数组表示到原点的最短距离，adj表示某一点最后出现的位置；  
bool vis[30005];
//访问数组
void spfa()
{
    for (int i = 0; i < 30005; i++) d[i] = INF;
    d[1] = 0;
    memset(vis, 0, sizeof(vis));
    int sta[30005];
    ////栈模拟，等价于用stack  
    int top = 0;
    vis[1] = 1;
    sta[++top] = 1;
    while (top){
        int pos = sta[top--];
        vis[pos] = 0;
        for (int i = adj[pos]; i != -1; i = e[i].next){
            int to = e[i].to;
            int cost = e[i].cost;
            if (d[to] > d[pos] + cost){
                d[to] = d[pos] + cost;
                if (vis[to] == 0){
                    sta[++top] = to;
                    vis[to] = 1;
                }
            }
        }
    }
    return;
}
int a, b, c;
int main()
{
    while (scanf("%d%d", &N, &M) != EOF){
        memset(vis,0,sizeof(vis));
        for (int i = 0; i < 30005; i ++) adj[i] = -1;
        //默认adj[i] = -1 时再往上找无边
        //多组数据必要的清空
        for (int i = 0; i < M; i++){
            scanf("%d%d%d", &a, &b, &c);
            e[i].to = b;
            e[i].cost = c;
            e[i].next = adj[a];
            //next记录下上一次从a出发在e[i]中的位置
            adj[a] = i;
            //记录下出发点a最后一次出现的位置
        }
        spfa();
        printf("%d\n", d[N]);
    }
}

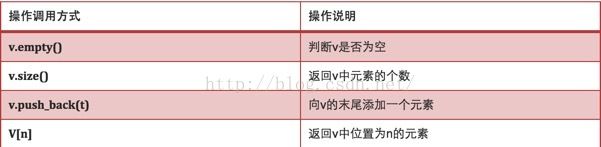
3、动态数组(vector)实现邻接表：

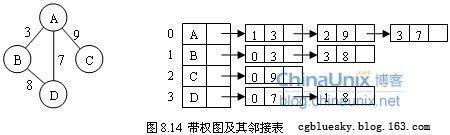
①定义：vector是STL中最常见的容器，它是一种顺序容器，支持随机访问。vector是一块连续分配的内存，从数据安排的角度来讲，和数组极其相似，不同的地方就是：数组是静态分配空间，一旦分配了空间的大小，就不可再改变了；而vector是动态分配空间，随着元素的不断插入，它会按照自身的一套机制不断扩充自身的容量。

②操作：

 ③图示：

 ④代码：以poj 3159为例 （vector 会超时）

#include 
#include 
#include 
#include 
#include 
#include 
#define INF 0x3f3f3f3f
#define MAXN 1000005
using namespace std;
int N, M;
struct node{
    int to, cost;
};
vector  e[30005];
int d[30005];
bool vis[30005];
int cmp(int a, int b){return a > b;}
void spfa()
{
    for (int i = 0; i < 30005; i++) d[i] = INF;
    d[0] = 0;
    d[1] = 0;
    memset(vis, 0, sizeof(vis));
    queue q;
    vis[1] = 1;
    q.push(1);
    while (!q.empty()){
        int tmp = q.front();
        q.pop();
        vis[tmp] = 0;
        for (int i = 0; i < e[tmp].size(); i++){
            node cur = e[tmp][i];
            if (d[cur.to] > d[tmp] + cur.cost){
                d[cur.to] = d[tmp] + cur.cost;
                if (vis[cur.to] == 0){
                    q.push(cur.to);
                    vis[cur.to] = 1;
                }
            }
        }
    }
    return;
}
int a, b, c;
node input;
int main()
{
    while (scanf("%d%d", &N, &M) != EOF){
        memset(vis,0,sizeof(vis));
        for (int i = 0; i < M; i++){
            scanf("%d%d%d", &a, &b, &c);
            input.to = b;
            input.cost = c;
            e[a].push_back(input);
            //存放到vector中
        }
        spfa();
        sort(d, d+N+1, cmp);
        printf("%d\n", d[0]);
    }
}

二、最短生成路的三种重要做法（Kruskal  Dijkstra  Bellman-Ford)：

1）Kruskal：(排序 + 并查集）

①算法核心：假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

②算法图示：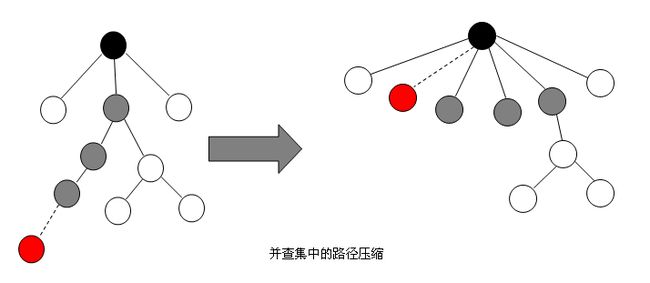

③代码实现：以POJ 2377为例（Kruskal 实现 mst)

#include  //定义输入／输出函数
#include  //定义各种数据类型最值常量
#include  //定义数学函数
#include  //定义杂项函数及内存分配函数
#include  //字符串处理
#include //算法
#include //队列
#include //栈
using namespace std;
int N, M;
int re[1005];           //源根
int finds(int x){       //找根函数
    if (re[x] == x) return x;
    else return re[x] = finds(re[x]);
}
struct node{
    int from, to, cost;
};
node a[20005];
int vis[1005];
int cmp(node a, node b){return a.cost > b.cost;}
long long sum;
int flag;

int main()
{
    while (scanf("%d%d", &N, &M) != EOF){
        for (int i = 0; i < M; i++)
            scanf("%d%d%d", &a[i].from, &a[i].to, &a[i].cost);
        sort(a, a+M, cmp);
        //读取输入
        for (int i = 0; i <= N; i++) re[i] = i;
        //根重置
        memset(vis, 0, sizeof(vis));
        //访问重置
        sum = flag = 0;
        for (int i = 0; i < M; i++){
            if (finds(a[i].from) == finds(a[i].to)) continue;
            //如果查找后两数根不相等，则进行以下程序
            re[finds(a[i].from)] = finds(a[i].to);
            //直接把一根连在另一根的生成树上
            vis[a[i].from] = 1;
            vis[a[i].to] = 1;
            sum += a[i].cost;
        }
        for (int i = 1; i <= N; i++){
            if (vis[i] == 0) flag = 1;
            if (finds(i) != finds(1)) flag = 1;
        }
        if (flag == 1) printf("-1\n");
        else printf("%lld\n", sum);
    }
}

2）Dijkstra：( 动态规划 + 数组 + 松弛 )

①算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则正常有权值，若u不是v的出边邻接点，则权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

②算法图示：

③算法代码：（以 poj2485 为例  简单 dij)

#include  //定义输入／输出函数
#include  //定义各种数据类型最值常量
#include  //定义数学函数
#include  //定义杂项函数及内存分配函数
#include  //字符串处理
#include //算法
#include //队列
#include //栈
#include //动态数组
using namespace std;
int T, N, pos, mins;
int map[505][505];
bool vis[505];
int low[505];
int cmp(int a, int b) {return a > b;}
int main()
{
    while (scanf("%d", &T) != EOF){
 		while (T--){
        memset(map, 0, sizeof(map));
        memset(low, 0, sizeof(low));
        memset(vis, 0, sizeof(vis));
        scanf("%d", &N);
        printf("N = %d\n", N);
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= N; j++)
                scanf("%d", &map[i][j]);
        for (int i = 1; i <= N; i++)
            low[i] = map[1][i];
        low[1] = 0;
        vis[1] = pos = 1;
        for (int i = 1; i < N; i++){
            mins = 65550;
            for (int j = 1; j <= N; j++)
                if (vis[j] == 0 && mins > low[j]){
                    mins = low[j];
                    pos = j;
                }
            //在d[N]中找到最小值的位置
            vis[pos] = 1;
            for (int j = 1; j <= N; j++){
                if(low[j] > map[pos][j] && vis[j] == 0)
                    low[j] = map[pos][j];
            }
            //用最小值的位置更新Low数组
        }
        //for (int i = 0; i <= N; i++) printf(" %d", low[i]);
        //printf("\n");
        sort(low, low + N + 1, cmp);
        for (int i = 0; i <= N; i++) printf(" %d", low[i]);
        printf("\n");
        printf("%d\n", low[0]);
    	}
    }
}

3）Bellman--Ford：( 优先队列  +  动态数组 + 松弛 )

①算法介绍：

给定图G(V, E)（其中V、E分别为图G的顶点集与边集），源点s，数组Distant[i]记录从源点s到顶点i的路径长度，初始化数组Distant[n]为, Distant[s]为0；

以下操作循环执行至多n-1次，n为顶点数：
对于每一条边e(u, v)，如果Distant[u] + w(u, v) < Distant[v]，则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值；
若上述操作没有对Distant进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环；

为了检测图中是否存在负环路，即权值之和小于0的环路。对于每一条边e(u, v)，如果存在Distant[u] + w(u, v) < Distant[v]的边，则图中存在负环路，即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。

可知，Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).

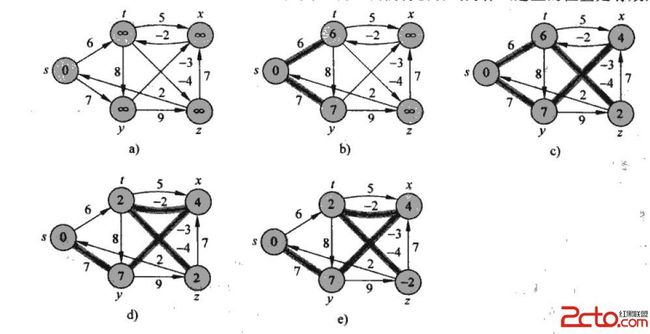
②算法流程：

第一，初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。
第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。
第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：d（v） > d (u) + w(u,v) 存在则赋值；

③算法图示：

④算法代码：（以poj 1511为例 数组模拟 + 队列 / 栈 + 双向图）

#include  //定义输入／输出函数
#include  //定义各种数据类型最值常量
#include  //定义数学函数
#include  //定义杂项函数及内存分配函数
#include  //字符串处理
#include //算法
#include //队列
#include //栈
const int INF = 0x3f3f3f3f;
using namespace std;
struct node{
    int to, cost;
    int next;
};
node e[2][1000005];
int N, P, Q;
int adj[2][1000005], d[1000005];
bool vis[1000005];
int a, b, c;
long long sum;
void spfa(int k)
{
    memset(vis, 0, sizeof(vis));
    memset(d, INF, sizeof(d));
    stack  s; 
    //开queue 也行，一样时间与内存
    s.push(1);
    d[1] = 0;
    vis[1] = 1;
    while (!s.empty()){
        int pos = s.top();
        s.pop();
        vis[pos] = 0;
        for (int i = adj[k][pos]; i!= -1; i = e[k][i].next){
            int to = e[k][i].to;
            int cost = e[k][i].cost;
            if (d[to] > d[pos] + cost){
                d[to] = d[pos] + cost;
                if (vis[to] == 0){
                    s.push(to);
                    vis[to] = 1;
                }
            }
        }
    }
}

int main()
{
    while (scanf("%d", &N) != EOF){
        while (N--){
            memset(adj, -1, sizeof(adj));
            memset(e, 0, sizeof(e));
            sum = 0;
            scanf("%d%d", &P, &Q);
            for (int i = 0; i < Q; i++){
                scanf("%d%d%d", &a, &b, &c);
                e[0][i].to = b;
                e[0][i].cost = c;
                e[0][i].next = adj[0][a];
                adj[0][a] = i;
                e[1][i].to = a;
                e[1][i].cost = c;
                e[1][i].next = adj[1][b];
                adj[1][b] = i;
            }
            
            spfa(0);
            for (int i = 1; i <= P; i++) sum += d[i];
            //printf("\n");
            spfa(1);
            for (int i = 1; i <= P; i++) sum += d[i];
            //printf("\n");
            printf("%lld\n", sum);
        }
    }
}