再谈数据结构（三）图

1 - 引言

图（Graph）描述的是一些个体之间的关系。与线性表和二叉树不同的是：这些个体之
间既不是前驱后继的顺序关系，也不是祖先后代的层次关系，而是错综复杂的网状关系。

图也是数据结构中经常使用的一种结构，让我们来学习一下使用图的算法吧

2 - 用DFS求连通块

例题6-12　油田（Oil Deposits, UVa 572）

输入一个m行n列的字符矩阵，统计字符“@”组成多少个八连块。如果两个字符“@”所在
的格子相邻（横、竖或者对角线方向），就说它们属于同一个八连块。

Sample Input
1 1
*
3 5
$\ast @\ast @\ast$
$\ast \ast @\ast \ast$
$\ast @\ast @\ast$
1 8
$@@\ast \ast \ast \ast @\ast$
5 5
$\ast \ast \ast \ast @$
$\ast @@\ast @$
$\ast @\ast \ast @$
$@@@\ast @$
$@@\ast \ast @$
0 0

Sample Output
0
1
2
2

【分析】
和前面的二叉树遍历类似，图也有DFS和BFS遍历。由于DFS更容易编写，一般用DFS找
连通块：从每个“@”格子出发，递归遍历它周围的“@”格子。每次访问一个格子时就给它写
上一个“连通分量编号”（即下面代码中的idx数组），这样就可以在访问之前检查它是否已经
有了编号，从而避免同一个格子访问多次：

#include
#include
const int maxn = 100 + 5;
char pic[maxn][maxn];
int m,n;
int idx[maxn][maxn];
void dfs(int r ,int c)
{

    if(r < 0 || r >= m  || c < 0 || c >= n) return; //“出界”的格子
    if(idx[r][c]>0 || pic[r][c]!='@') return; //不是“@”或者已经访问过的格子

    idx[r][c]= 1;  //连通分量编号

    for(int dr = -1; dr<=1; dr++)
        for(int dc=-1;dc<=1;dc++)
            if(dr!=0||dc!=0) dfs(r+dr,c+dc);
}

int main(){



    while(scanf("%d%d", &m,&n)==2&&m&&n){

        for(int i=0;i

上面的代码用一个二重循环来找到当前格子的相邻8个格子，也可以用常量数组或者写8
条DFS调用，读者可以根据自己的喜好选用。这道题目的算法有个好听的名字：种子填充
（floodfill）。有兴趣的读者还可以看看维基百科(3)中的动画，对DFS和BFS实现的种子填充
有一个更直观的认识。

例题6-13　古代象形符号（Ancient Messages, World Finals 2011, UVa 1103）

本题的目的是识别3000年前古埃及用到的6种象形文字，如图

每组数据包含一个H行W列的字符矩阵（H≤200，W≤50），每个字符为4个相邻像素点的
十六进制（例如，10011100对应的字符就是9c）。转化为二进制后1表示黑点，0表示白点。

输入满足：

• 不会出现上述6种符号之外的其他符号。
• 输入至少包含一个符号，且每个黑像素都属于一个符号。
• 每个符号都是一个四连块，并且不同符号不会相互接触，也不会相互包含。
• 如果两个黑像素有公共顶点，则它们一定有一个相同的相邻黑像素（有公共边）。
• 符号的形状一定和表6-9中的图形拓扑等价（可以随意拉伸但不能拉断）。

【分析】
“随意拉伸但不能拉断”是一个让人头疼的条件。怎么办呢？看来不能拘泥于细节，而要
从全局考虑，找到一个易于计算，而且在“随意拉伸”时还不会改变的“特征量”，通过计算和
比较“特征量”完成识别。题目说过，每个符号都是一个四连块，即所有黑点都连在一起，而
中间有一些白色的“洞”。数一数就能发现，题目表中的6个符号从左到右依次有
1，3，5，4，0，2个洞，各不相同。这样，只需要数一数输入的符号有几个“白洞”，就能准
确地知道它是哪个符号了。

#include 
#include 
using namespace std;
 
int num[210][210];
int h, w, count;
 
int ans[8];
char str[] = {'A', 'D', 'J', 'K', 'S', 'W'};
int bin[][4] = {{0,0,0,0},  //0
				{0,0,0,1},  //1
				{0,0,1,0},  //2
				{0,0,1,1},  //3
				{0,1,0,0},  //4
				{0,1,0,1},  //5
				{0,1,1,0},  //6
				{0,1,1,1},  //7
				{1,0,0,0},  //8
				{1,0,0,1},  //9
				{1,0,1,0},  //a
				{1,0,1,1},  //b
				{1,1,0,0},  //c
				{1,1,0,1},  //d
				{1,1,1,0},  //e
				{1,1,1,1}}; //f
 
 
bool cheak(int x, int y)
{
	if((x >= 0 && x <= h + 1) && (y >= 0 && y <= w + 1))
		return true;
	else
		return false;
}
 
void dfs(int x, int y)
{
	if(!cheak(x, y) || num[x][y] != 0)
		return;
	num[x][y] = -1;
//	cout << x << ' ' << y << endl;
	dfs(x - 1, y);
	dfs(x, y + 1);
	dfs(x + 1, y);
	dfs(x, y - 1);
}
 
void DFS(int x, int y)
{
	if(!cheak(x, y) || num[x][y] == -1)
		return;
 
	if(num[x][y] == 0)  //找到空洞
	{
		count++;
		dfs(x, y);
		return;
	}
	num[x][y] = -1;
	DFS(x - 1, y);
	DFS(x, y + 1);
	DFS(x + 1, y);
	DFS(x, y - 1);
}
 
int main()
{
	freopen("1103.txt", "r", stdin);
	int t = 0, i, j;
	char ch;
	while(cin >> h >> w)
	{
		if(h == 0 && w == 0)
			break;
		memset(num, 0, sizeof(num));
		memset(ans, 0, sizeof(ans));
		for(i = 0; i < h; i++)
		{
			for(j = 0; j < w; j++)
			{
				cin >> ch;
				if(ch >= '0' && ch <= '9')      //转换成二进制的
				{
					int l = 0;
					for(int k = j * 4 + 1; k <= j * 4 + 4; k++)
						num[i + 1][k] = bin[ch - '0'][l++];
				} else if(ch >= 'a' && ch <= 'f')
				{
					int l = 0;
					for(int k = j * 4 + 1; k <= j * 4 + 4; k++)
						num[i + 1][k] = bin[ch - 'a' + 10][l++];
				}
			}
		}
 
		w = w * 4;                   //宽 * 4
 
		dfs(0, 0);                   //分离文字
		cout << "Case " << ++t << ": ";
		for(i = 1; i <= h; i++)
		{
			for(j = 1; j <= w; j++)
			{
				
				if(num[i][j] == 1)       //找到一个文字
				{
					count = 0;
					DFS(i, j);
					if(count == 0)
						ans[5]++;
					if(count == 1)
						ans[0]++;
					if(count == 2)
						ans[3]++;
					if(count == 3)
						ans[2]++;
					if(count == 4)
						ans[4]++;
					if(count == 5)
						ans[1]++;
				}
				
			}
		}
		for(i = 0; i < 6; i++)
		{
			while(ans[i]--)
				cout << str[i];
		}
		cout << endl;
	}
	return 0;
}

3 - 用BFS求最短路

还记得二叉树的BFS吗？结点的访问顺序恰好是它们到根结点距离从小到大的顺序。类
似地，也可以用BFS来按照到起点的距离顺序遍历迷宫图。

例如，假定起点在左上角，就从左上角开始用BFS遍历迷宫图，逐步计算出它到每个结
点的最短路距离，以及这些最短路径上每个结点的“前一个结点
　　
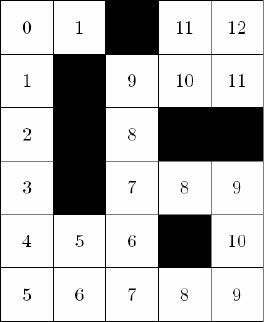
注意，如果把图中的箭头理解成“指向父亲的指针”，那么迷宫中的格子就变
成了一棵树——除了起点之外，每个结点恰好有一个父亲。如果看不出来，可以把这棵树画
成如图所示的样子。这棵树称为最短路树，或者BFS树。

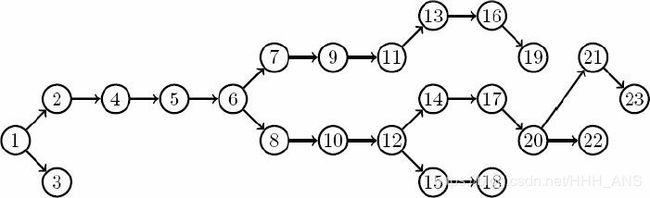
下面我们来看一道例题学会BFS的应用

例题6-14　Abbott的复仇（Abbott’s Revenge, ACM/ICPC World Finals 2000, UVa 816)

有一个最多包含9*9个交叉点的迷宫。输入起点、离开起点时的朝向和终点，求一条最
短路（多解时任意输出一个即可）。
Sample Input
3 1 N 3 3
1 1 WL NR *
1 2 WLF NR ER *
1 3 NL ER *
2 1 SL WR NF *
2 2 SL WF ELF *
2 3 SFR EL *
0

Sample Output
(3,1) (2,1) (1,1) (1,2) (2,2) (2,3) (1,3) (1,2) (1,1) (2,1)
(2,2) (1,2) (1,3) (2,3) (3,3)

这个迷宫的特殊之处在于：进入一个交叉点的方向（用NEWS这4个字母分别表示北东西南，即上右左下）不同，允许出去的方向也不同。例如，1 2 WLF NR ER 表示交叉点(1,2)（上数第1行，左数第2列）有3个路标（字符“”只是结束标志），如果进入该交叉点时的朝向为W（即朝左），则可以左转（L）或者直行（F）；如果进入时朝向为N或者E则只能右转（R）

【分析】
本题和普通的迷宫在本质上是一样的，但是由于“朝向”也起到了关键作用，所以需要用
一个三元组(r, c, dir)表示“位于(r,c)，面朝dir”这个状态。假设入口位置为(r0, c0)，朝向为
dir，则初始状态并不是(r0, c0, dir)，而是(r1, c1, dir)，其中，(r1,c1)是(r0,c0)沿着方向dir走一
步之后的坐标。此处用d[r][c][dir]表示初始状态到(r,c,dir)的最短路长度，并且用p[r][c][dir]
保存了状态(r,c,dir)在BFS树中的父结点。
注：很多复杂的迷宫问题都可以转化为最短路问题，然后用BFS求解。在套用
BFS框架之前，需要先搞清楚图中的“结点”包含哪些内容。

本题非常重要，强烈建议能搞懂所有细节，并能独立编写程序。

#include
#include
#include
#include
using namespace std;

struct Node {
  int r, c, dir; // 站在(r,c)，面朝方向dir(0~3分别表示N, E, S, W)
  Node(int r=0, int c=0, int dir=0):r(r),c(c),dir(dir) {}
};

const int maxn = 10;
const char* dirs = "NESW"; // 顺时针旋转
const char* turns = "FLR";

int has_edge[maxn][maxn][4][3];//保存每一个坐标的具体转向方式
int d[maxn][maxn][4];//用来累加起点到终点的距离
Node p[maxn][maxn][4];//p[r][c][dir]表示了(r,c,dir)在BFS树中的父节点
int r0, c0, dir, r1, c1, r2, c2;

int dir_id(char c) { return strchr(dirs, c) - dirs; }//返回c在dirs的位置
int turn_id(char c) { return strchr(turns, c) - turns; }

const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};

Node walk(const Node& u, int turn) {
  int dir = u.dir;
  if(turn == 1) dir = (dir + 3) % 4; // 逆时针，表示左转
  if(turn == 2) dir = (dir + 1) % 4; // 顺时针，表示右转
  return Node(u.r + dr[dir], u.c + dc[dir], dir);
}

//判断坐标是否出界
bool inside(int r, int c) {
  return r >= 1 && r <= 9 && c >= 1 && c <= 9;
}

//初始化起点，终点和每一个坐标的转向
bool read_case() {
  char s[99], s2[99];
  //s是指当前的流程，r0表示起始行，c0表示起始列，s2起始方向，r2表示目标行，c2表示目标列
  if(scanf("%d%d%s%d%d", &r0, &c0, s2, &r2, &c2) != 5) return false;

  dir = dir_id(s2[0]);//方向在字符串dirs中的位置
  r1 = r0 + dr[dir];//第一步之后的行坐标
  c1 = c0 + dc[dir];//第二步之后的列坐标

  memset(has_edge, 0, sizeof(has_edge));
  for(;;) {
    int r, c;
    scanf("%d", &r);
    if(r == 0) break;
    scanf("%d", &c);
    while(scanf("%s", s) == 1 && s[0] != '*') {
      for(int i = 1; i < strlen(s); i++)
        has_edge[r][c][dir_id(s[0])][turn_id(s[i])] = 1;
    }
  }
  return true;
}

void print_ans(Node u) {
  // 从目标结点逆序追溯到初始结点
  vector nodes;
  for(;;) {
    nodes.push_back(u);
    if(d[u.r][u.c][u.dir] == 0) break;//说明找到了终点
    u = p[u.r][u.c][u.dir];
  }
  nodes.push_back(Node(r0, c0, dir));

  // 打印解，每行10个
  int cnt = 0;
  for(int i = nodes.size()-1; i >= 0; i--) {
    printf(" (%d,%d) ", nodes[i].r, nodes[i].c);
    if(++cnt == 10){
        printf("\n");
    }
  }
}

//使用BFS输出
void solve() {
  queue q;
  memset(d, -1, sizeof(d));
  //第一步之后，处于（2,1，N）的状态
  Node u(r1, c1, dir);//走了一步之后的坐标
  d[u.r][u.c][u.dir] = 0;
  q.push(u);
  while(!q.empty()) {
    Node u = q.front(); q.pop();
    if(u.r == r2 && u.c == c2) { print_ans(u); return; }
    //判断当前坐标点，在当前转向的三个方向哪个是可以行使的？
    for(int i = 0; i < 3; i++) {
      Node v = walk(u, i);
      //v是u坐标行走一步之后的坐标，走到终点没有初始化，has_edge值为0，不进入循环
      if(has_edge[u.r][u.c][u.dir][i] && inside(v.r, v.c) && d[v.r][v.c][v.dir] < 0) {
        d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] + 1;//累加1，最后得出起点到终点的距离
        p[v.r][v.c][v.dir] = u;//表示v的父节点是u
        q.push(v);
      }
    }
  }
  printf("  No Solution Possible\n");
}

int main() {
  while(read_case()) {
    solve();
  }
  return 0;
}

4 - 拓扑排序

例题6-15　给任务排序（Ordering Tasks, UVa 10305）

Sample Input
5 4
1 2
2 3
1 3
1 5
0 0
Sample Output（拓扑排序答案不只一种）
1 4 2 5 3
思路：

拓扑排序。先在草稿纸上画了个图，每一个数字指向它后面对应的数字，用样例来说，初始化vis[]都为0，从1开始遍历，vis[1]标记为-1，找到存在1指向下一个数字的路径，假如这个点的vis为-1，那么存在有向环，失效退出，如果不是有向环且这个结点没有被访问过，则从这个点开始搜索。搜索完后标记当前搜索结点的vis为1，并压入栈。

#include
#include
#include
using namespace std;
int n,m;
int task[101][101];
int vis[101];
stack s;
void dfs(int u)
{
    vis[u]=-1;
    for(int i=1;i<=n;i++)
    {
        if(task[u][i]==1)
        {
            if(vis[i]==-1)return;
            else if(!vis[i])dfs(i);
        }
    }
    s.push(u);
    vis[u]=1;
}
int main()
{
    while(cin>>n>>m&&(m||n))
    {
        memset(task,0,sizeof(task));
        memset(vis,0,sizeof(vis));
        int i,x,y;
        for(i=1;i<=m;i++)
        {
            cin>>x>>y;
            task[x][y]=1;
        }
        for(i=1;i<=n;i++)
        {
            if(vis[i]!=1)dfs(i);
        }
        while(!s.empty())
        {
            cout<

5 - 欧拉回路

例题6-16　单词（Play On Words, UVa 10129）

题目大意翻译：
有一些秘密的门包含着非常有趣的单词迷题， 考古学家队伍必须解决它们才能够打开大门。 因为没有其他方法能偶打开这些门， 所以解决那些迷题对我们非常重要。
在每个门上有很多个有磁力的盘子，盘子上面写着单词。 必须重新移动放置这些盘子，让它们形成一个队列：队列中，除了第一个单词，每个单词的开头和上一个单词的结尾字母
一样。例如， motorola的后面可以接上acm。
你的任务是写一个程序， 读入一系列单词，然后计算确定它们是否有可能被排成这样的队列。

样例输入：

3
2
acm
ibm
3
acm
malform
mouse
2
ok
ok

样例输出：

The door cannot be opened.
Ordering is possible.
The door cannot be opened.

分析与总结：
把字母看作结点，单词看成有向边，则问题有解，当且仅当图中有欧拉路径。前面讲
过，有向图存在欧拉道路的条件有两个：底图（忽略边方向后得到的无向图）连通，且度数
满足上面讨论过的条件。判断连通的方法有两种，一是之前介绍过的DFS，二是并查集。

在这里给出用DFS编写的代码：

#include
#include
#include
#include

using namespace std;

void connected(int v);
bool degree_to_meet();
void init();

const int MAXN = 26 + 4;
//二维数组g用来存边，    in[i]来存i的出度，out同理，   cnt用来在DFS之后判断是否访问了所有的点，也就是图是否连通
int g[MAXN][MAXN], in[MAXN], out[MAXN], cnt;
set chr;		//用来存所有的点
bool vis[MAXN];		//DFS时用来判断是否访问过i

int main()
{
	//freopen("input.txt","r",stdin);
	//freopen("output.txt","w",stdout);
	int n, m;
	string s;
	cin >> n;
	while (n--)
	{
		cin >> m;
		while (m--)							//输入初始化
		{
			cin >> s;
			int ch_in = s[0] - 'a', ch_out = s[s.size()-1] - 'a';
			g[ch_in][ch_out] = 1;g[ch_out][ch_in] = 1;
			in[ch_in]++; out[ch_out]++;
			chr.insert(ch_in); chr.insert(ch_out);
		}
		cnt = 1;
		connected(*chr.begin());		//进行DFS
		if (cnt == chr.size() && degree_to_meet()) //判断两个条件是否满足
			cout << "Ordering is possible.\n";
		else cout << "The door cannot be opened.\n";
		init();
	}
	return 0;
}

bool degree_to_meet()				//判断是否满足欧拉通路（回路）出度和入度的关系
{
	bool ch_begin = false, ch_end = false;
	for (set::iterator it = chr.begin(); it != chr.end(); it++)
	{
		int dv = in[*it] - out[*it];
		if (dv)
		{	//如果存在出入度之差不为1或-1，或者多个出入度为1或-1的点，则说明不是欧拉通路
			if ((dv != 1 && dv != -1) || (ch_begin && dv == 1) || (ch_end && dv == -1))
				return false;
			if (dv == 1) ch_begin = true;
			if (dv == -1) ch_end = true;
		}
	}
	return true;
}

void connected(int v)			//进行DFS
{
	vis[v] = true;
	for (set::iterator it = chr.begin(); it != chr.end(); it++)
	{
		if (g[v][*it] && !vis[*it])
		{
			cnt++;				//每次访问一个新的点都要计数，以便以后判断是否所有点都被访问
			connected(*it);
		}
	}
	return ;
}

void init()			//初始化所有数组和set
{
	chr.clear();
	memset(g, 0, sizeof(g));
	memset(in, 0, sizeof(in));
	memset(out, 0, sizeof(out));
	memset(vis, 0, sizeof(vis));
}

6 - 总结

图的算法大多是基于BFS或者DFS的特点编写的，在解决图的问题的时候应该灵活的掌握这两种遍历的特点和编写框架