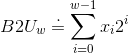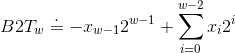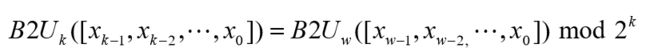《深入理解计算机系统》(2) 整数

整型数据类型

C语言支持多种整型数据类型。这些整型数据类型的典型取值范围大多是固定的，除了 long 之外：long 在 32 位机器上用 4 个字节表示，而在 64 位机器上用 8 个字节表示。

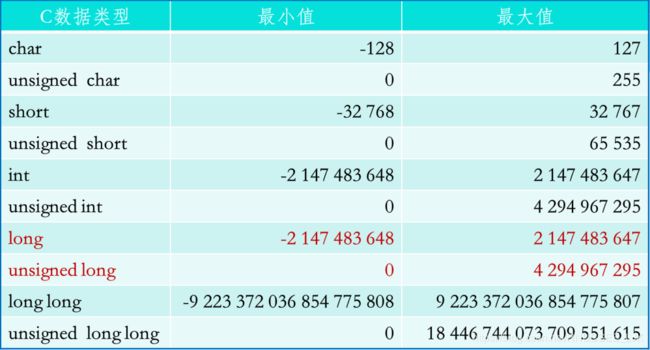C中典型整型数据的取值范围(32位机) 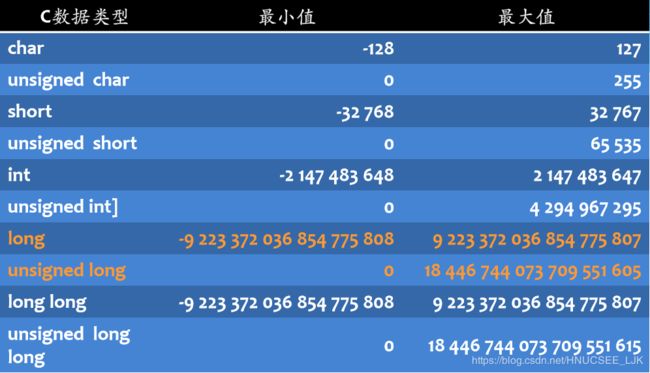 C中典型整型数据的取值范围(64位机) 

无符号数编码

对于长度为 w 的位向量 （或表示为  ），只要把  看作一个二进制表示的数，就是  的无符号表示。二进制转无符号数可以由函数 （Binary to Unsigned）来表示，即

对于一个 w 位的无符号数，它能表示的范围为 ，介于范围内的数的 w 位值编码是唯一的。

有符号数编码

• 补码

无符号数只能表示非负数，若要表示负数，就可以用补码。补码的最高有效位是符号位，它的权重是负的，为 。若符号位为 1，表示值为负；若符号位为 0，表示值为正。二进制转补码可以由函数 （Binary to Two's-complement）表示，即

对一个补码表示的数 x 取补，就相当于求 -x。求补的方式是，将每个位的 0 变为 1、1 变为 0 后加 1。如对 1010（十进制为 -6） 取补，首先将每个位取反，得到0101，将 0101 加 1 后得到 0110（十进制为 6）。

对于一个 w 位的补码，它能表示的范围为 ，介于范围内的数的 w 位值编码是唯一的。可以看到，补码的范围是不对称的，有 ，也就是说， 没有与之对应的正数。

• 反码与原码

有符号数还可以由反码或原码表示。反码除了最高有效位的权是  以外，它和补码是一样的；而原码的最高有效位是符号位，剩下的位以无符号数来解释。

对于 w 位的反码或原码，两者能表示的范围都为 。反码与补码都有一个奇怪的现象：对于数字 0 有两种不同的编码方式。这两种表示方法将 [00...0] 解释为 +0，而将 [10...0] 解释为 -0。

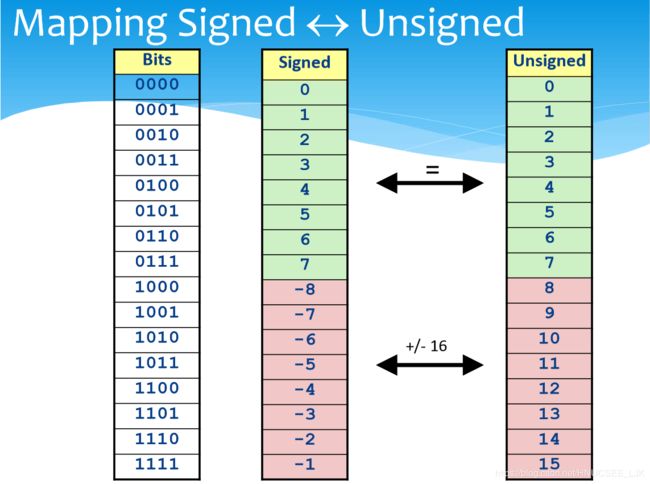
无符号数与有符号数之间的转换

上面是无符号整数与有符号整数的映射图，这里的有符号数采用的是补码。处理相同长度的无符号数与有符号数之间的相互转换的一般规则是：数值可能会改变，但是位模式不变。通过总结我们得到

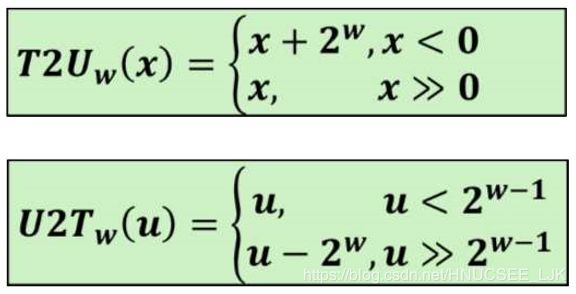>> 应为 ≥

另外，值得注意的是，在 C 语言中执行一个运算时，当一个运算数是无符号的时候，另一个运算数将会被隐式强制转换位无符号数，即假设两个数都是非负的来执行这个运算。这可能会导致一些奇特的错误。

扩展与截断

将一个位数相对较小的数据类型转换到一个位数相对较大的类型，并且值保持不变，叫做扩展。

无符号数的扩展方法称为零扩展，只需简单地在表示的开头补 0 到相应的扩展位数，如要将 1010 扩展至 8 位表示，经零扩展后，得到 00001010；补码的扩展方法称为符号扩展，规则是在表示的开头补符号位的值到相应的扩展位数，如要将 1010 扩展至 8 位表示，只要在开头补上符号位 1，得到 11111010，若符号位为 0，那么就同样补 0。

而将一个位数相对较大的数据类型转换到一个位数相对较小的类型，叫做截断。

将一个 w 位的数截断为 k 位，只需简单地保留低 k 位、舍弃高 w-k 位即可。截断可能导致数值的变化——这也是溢出的一种形式，对于一个无符号数 x，截断它到 k 位就相当于计算 ；对于一个补码 x，截断它到 k 位，与 类似。

无符号数截断

 

补码有符号数截断

整数运算

• 无符号加法

对于两个 w 位无符号整数 x 与 y，满足 ，x + y 的结果可能的范围为 ，表示这个结果可能需要 w+1 位。然而，编程语言通常只支持固定精度的计算（即位数固定），所以，机器只能简单地舍弃 x+y 的 w+1 位表示的最高位，而这种整数结果不能够完整地放到数据类型限定的位数中的情况，被称为算术运算溢出。比如当 x = 9，y = 12，w = 4 时，x、y 的位表示分别为 1001 与 1100，x + y = 21 的 5 位长的表示为 10101，然而，固定的精度使得机器不得不舍弃最高位的 1，得到 0101，也就是十进制的 5。

同时，无符号运算可以被视为一种模运算，舍弃最高位的无符号加法等价于计算和后模 。这可以从刚刚的例子看出：21 mod 16 = 5。一般来说，如果 x+y 没有产生进位，即 ，那么舍弃最高位并不会改变结果的数值；而如果 ，x+y 产生了进位，导致结果溢出，舍弃最高位 1 就相当于从和中减去了 ，刚好得到的就是 x+y 的和模  的结果。

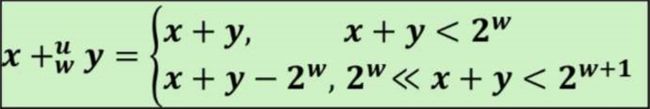<< 应为 ≤

因此，在 C 语言中，要判定 x+y 是否溢出，可以通过如下函数来判断：

int isOverflow(unsigned x, unsigned y){
    return x + y >= x; //若无溢出则返回1
}

• 补码加法

两个数的 w 位补码之和与无符号数之和有完全相同的位级表示，而有两者之间的差别就在于解释位向量时的方法不同，即补码加法将结果的位向量解释为补码，而无符号加法将其解释为无符号数。补码加法表示为 ，补码加法的结果有

若将  写成 ， 写成 ，根据  中无符号加法的模  的特性，可以将上式变换为

补码加法也会产生溢出现象。其中，当 x 与 y 都是负数，但是两者补码加法的和大于 0 时，称为产生了负溢出；当 x 与 y 都是整数，但是两者补码加法的和小于 0 时，称为产生了正溢出。只有当结果的 w+1 位表示的值在  之内，得到的才是正确结果。

• 补码的非

对于  中的补码 x，它的非运算的结果，即它的加法逆元，为 -x。比较特殊的是当 x =  时，在 w 位的限制之下，并没有一个能够与之对应的  来成为它的非运算结果。事实上，，于是我们声明，当 x =  时，x 的非运算的结果即是它本身。

另外，-x 实际上相当于对 x 求补码，即 -x = ~x + 1。通过这个等式，我们也可以得到当 x =  时，-x =  的事实。

• 无符号乘法

对于两个 w 位无符号整数 x 与 y，x * y 可能产生位数为 2w 的数。然而，与加法相仿，结果只能由 w 位来表示。根据无符号数截断的性质，将一个无符号数截断至 w 位相当于这个数模 ，我们可以得到

• 补码乘法

两个数的 w 位补码的完整的乘积位级表示与无符号乘法不同，但截断后的乘积的位级表示与无符号乘法相同，所以，机器简单地对两个补码进行无符号乘法，并将截断后的位向量解读为补码。结果为

根据补码加法将 x 表示为  的思路可以证明。

• 乘以常数的乘法

大多数机器的整数乘法指令速度相当慢，而其他整数运算（如加法、减法、位级运算和移位）的速度相当快。事实上，，并且无论是无符号运算还是补码运算，无溢出还是有溢出，该等式都是成立的，编译器就可以利用这个等式来优化乘以一个常数的乘法。

对于如 x * 14 这个式子，利用等式  ，可以将乘法改写为 (x << 3) + (x << 2) + (x << 1)，实现了将一个乘法替换为三个移位和两个加法，这是相当划算的。另外，如果列出等式 ，可以将乘法改写为 (x << 4) - (x << 1)，这样只需要两个移位和一个减法。编译器一般来说会自动进行这种优化。

• 除以 2 的幂的除法

大多数的机器的整数除法比整数乘法还要慢。对于除以 2 的幂的除法，我们同样可以用移位运算来实现。

对于无符号数，由于整数除法总是舍入到 0，而逻辑右移也总是舍入到 0，所以我们用逻辑右移来替代。

对于有符号数，由于要维护数的符号，所以采用算术右移。对于不需要舍入的情况，结果是正确的；但对于需要舍入的情况，即进行算术右移时，值为 1 的最低有效位被舍弃的情况，移位导致结果向下舍入，而不是整数除法的向 0 舍入。要修正这个问题，需要先将被除数 x 加上一个偏置量 ，k 为 2 的指数，然后再进行算术右移 x >> k，得到的就是正确的结果了。

(x < 0 ? (x + (1 << k) - 1) : x) >> k
//补码除以2的幂时的C语言表达式
//当然，C会自动修正