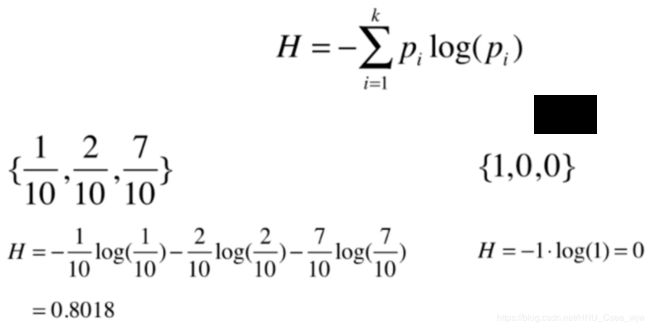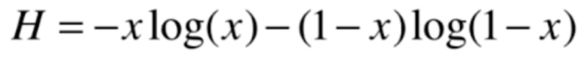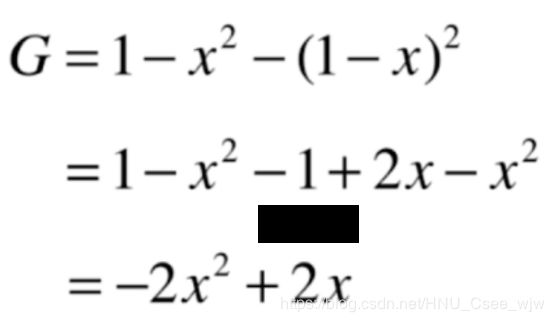Python遇见机器学习 ---- 决策树 Decision Tree
综述
“独木难成林”
本文采用编译器:jupyter
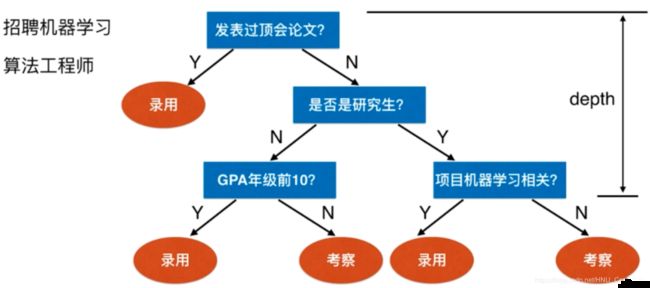
决策树 (decision tree) 是一类常见的机器学习方法,顾名思义,决策树是基于树结构来进行决策的,这恰是人类在面临决 策问题时一种很自然的处理机制。
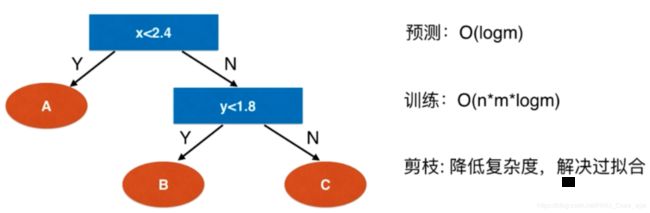
例如,我们要对“是否录用他作为机器学习算法工程师?”这样的问题进行决策时,通常会进行一系列的判断或“子决策”:我们先看“他是否发表过顶会论文?”如果是“没有”,则再看“是否是研究生?”如果是“是研究生”,再判断“他的项目是否和机器学习相关?”......最终我们得出决策。过程如图:
很明显,决策树是一种非参数学习算法,天然的可以解决多分类问题(也可以解决回归问题),并且得到的结果具有非常好的可解释性。
01 scikit-learn中的决策树
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:] # 取后两个特征
y = iris.target
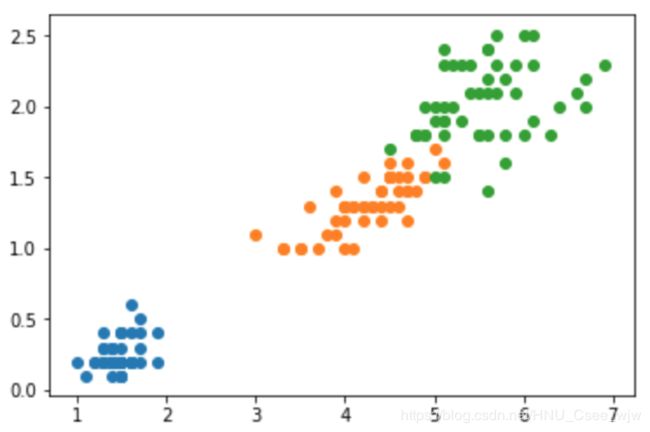
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
dt_clf.fit(X, y)
"""
Out[4]:
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
"""
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
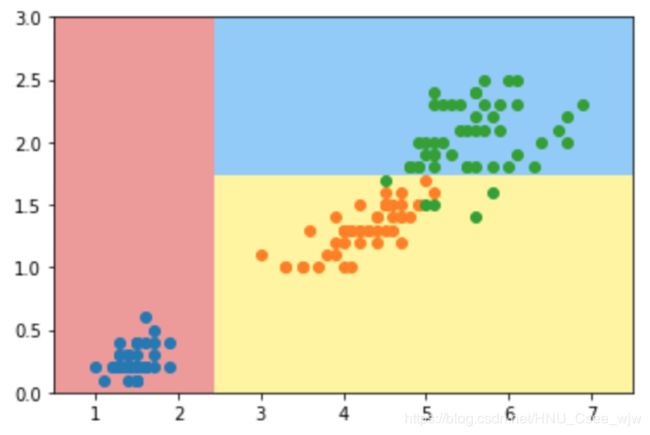
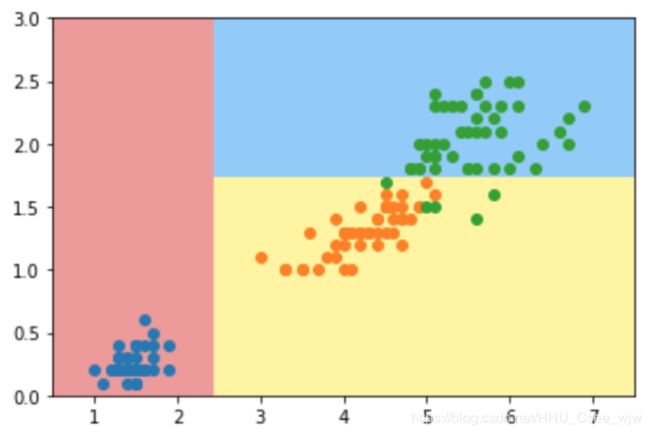
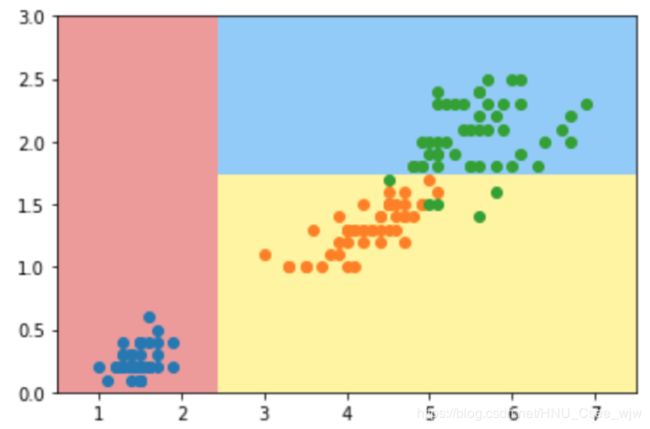
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
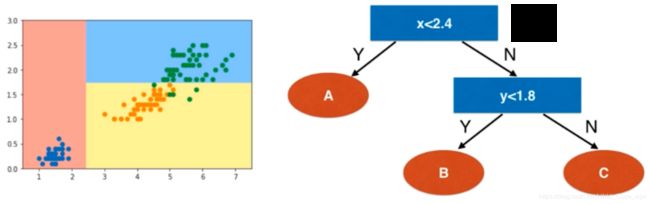
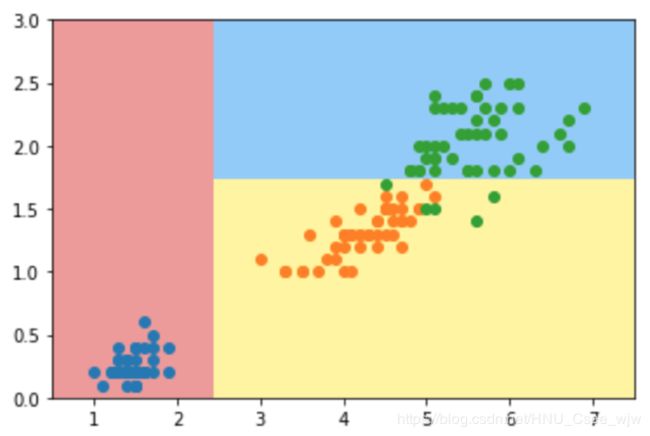
plt.show()我们的到的决策树如下:
02 信息熵
经过简单的实践时候我们应该好奇构造一颗决策树的方法,即每个节点在哪个维度上做划分?以及某个维度在哪个值上做划分?
决策树中最常用的标准之一是信息熵,信息熵表示的是随机变量不确定度的度量。熵越大,数据的不确定性越高;熵越小,数据的不确定性越低。表达式如下:
对于二分类任务:
所以对于上面提出的两个问题,我们的目的是使得划分后的信息熵降低
import numpy as np
import matplotlib.pyplot as plt
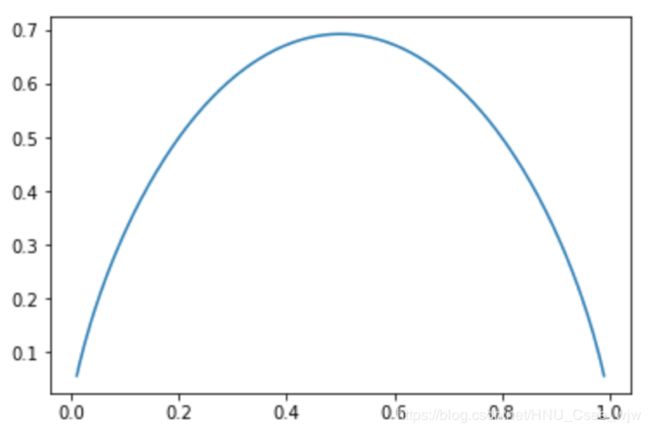
def entropy(p):
return -p * np.log(p) - (1-p) * np.log(1-p)
x = np.linspace(0.01, 0.99, 200)
plt.plot(x, entropy(x))
plt.show()03 使用信息熵寻找最优划分
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:] # 取后两个特征
y = iris.target
from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
dt_clf.fit(X, y)
"""
Out[4]:
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
"""
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()模拟使用信息熵进行划分
# d:维度 value:阈值
def split(X, y, d, value):
index_a = (X[:,d] <= value)
index_b = (X[:,d] > value)
return X[index_a], X[index_b], y[index_a], y[index_b]
# 计算阈值
from collections import Counter
from math import log
def entropy(y):
counter = Counter(y) # 包装成字典
res = 0.0
for num in counter.values():
p = num / len(y)
res += -p * log(p)
return res
def try_split(X, y):
best_entropy = float('inf')
best_d, best_v = -1, -1
# 寻找用来划分用的的维度和阈值
# 阈值取相邻大小两个点的中间值
for d in range(X.shape[1]):
sorted_index = np.argsort(X[:,d])
# 对每个样本遍历
for i in range(1, len(X)):
if X[sorted_index[i-1], d] != X[sorted_index[i], d]:
v = (X[sorted_index[i-1], d] + X[sorted_index[i], d]) / 2
# 按照此维度与阈值进行划分
X_l, X_r, y_l, y_r = split(X, y, d, v)
# 计算信息熵
e = entropy(y_l) + entropy(y_r)
if e < best_entropy:
best_entropy, best_d, best_v = e, d, v
return best_entropy, best_d, best_v
best_entropy, best_d, best_v = try_split(X, y)
print("best_entropy = ", best_entropy)
print("best_d = ", best_d)
print("best_v = ", best_v)
# 对比之前的边界图像可以看出,第一个划分的位置就是在横轴2.45附近
best_entropy = 0.6931471805599453
best_d = 0
best_v = 2.45
X1_l, X1_r, y1_l, y1_r = split(X, y, best_d, best_v)
entropy(y1_l) # 第一次划分成功把一个数据划分出来
# Out[14]:
# 0.0
entropy(y1_r)
# Out[15]:
# 0.6931471805599453
best_entropy2, best_d2, best_v2 = try_split(X1_r, y1_r)
print("best_entropy2 = ", best_entropy2)
print("best_d2 = ", best_d2)
print("best_v2 = ", best_v2)
# 对比之前的边界图像可以看出,第二个划分的位置就是在y轴1.75附近
best_entropy2 = 0.4132278899361904
best_d2 = 1
best_v2 = 1.75
X2_l, X2_r, y2_l, y2_r = split(X1_r, y1_r, best_d2, best_v2)
entropy(y2_l)
# Out[19]:
# 0.30849545083110386
entropy(y2_r)
# Out[20]:
# 0.10473243910508653
# 可以继续往更深的地方划分......04 基尼系数
除了信息熵之外,还有另一种划分的标准,称为基尼系数。
和信息熵相比,大多时候二者没有特别的效果优劣,scikit-learn中默认为基尼系数。
对于二分类问题:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:] # 取后两个特征
y = iris.target
from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="gini")
dt_clf.fit(X, y)
"""
Out[3]:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
"""
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
# 与信息熵得出的结果是相同的模拟使用基尼系数划分
from collections import Counter
from math import log
def split(X, y, d, value):
index_a = (X[:,d] <= value)
index_b = (X[:,d] > value)
return X[index_a], X[index_b], y[index_a], y[index_b]
def gini(y):
counter = Counter(y)
res = 1.0
for num in counter.values():
p = num / len(y)
res -= p**2
return res
def try_split(X, y):
best_g = 1e9
best_d, best_v = -1, -1
# 寻找用来划分用的的维度和阈值
# 阈值取相邻大小两个点的中间值
for d in range(X.shape[1]):
sorted_index = np.argsort(X[:,d])
# 对每个样本遍历
for i in range(1, len(X)):
if X[sorted_index[i-1], d] != X[sorted_index[i], d]:
v = (X[sorted_index[i-1], d] + X[sorted_index[i], d]) / 2
# 按照此维度与阈值进行划分
X_l, X_r, y_l, y_r = split(X, y, d, v)
# 计算信息熵
g = gini(y_l) + gini(y_r)
if g < best_g:
best_g, best_d, best_v = g, d, v
return best_g, best_d, best_v
best_g, best_d, best_v = try_split(X, y)
print("best_g = ", best_g)
print("best_d = ", best_d)
print("best_v = ", best_v)
best_g = 0.5
best_d = 0
best_v = 2.45
X1_l, X1_r, y1_l, y1_r = split(X, y, best_d, best_v)
gini(y1_l) # 第一次划分成功把一个数据划分出来
# Out[9]:
# 0.0
gini(y1_r)
# Out[10]:
# 0.5
best_g2, best_d2, best_v2 = try_split(X1_r, y1_r)
print("best_g2 = ", best_g2)
print("best_d2 = ", best_d2)
print("best_v2 = ", best_v2)
best_g2 = 0.2105714900645938
best_d2 = 1
best_v2 = 1.75
X2_l, X2_r, y2_l, y2_r = split(X1_r, y1_r, best_d2, best_v2)
gini(y2_l)
# Out[13]:
# 0.1680384087791495
gini(y2_r)
# Out[14]:
# 0.0425330812854443105 CART和决策树的超参数
决策树复杂度分析:
可以通过设置决策树的CART参数来降低复杂度。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X, y = datasets.make_moons()
X, y = datasets.make_moons(noise=0.25, random_state=666)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier() # 划分标准默认为基尼系数
dt_clf.fit(X, y)
"""
Out[6]:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
"""
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
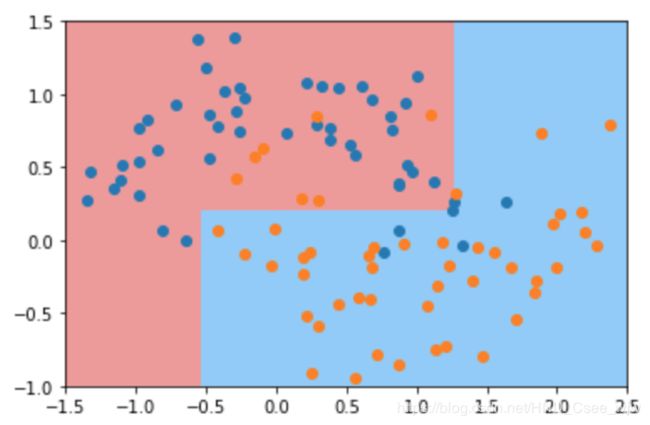
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
# 可以看出,产生了过拟合dt_clf2 = DecisionTreeClassifier(max_depth=2)
dt_clf2.fit(X, y)
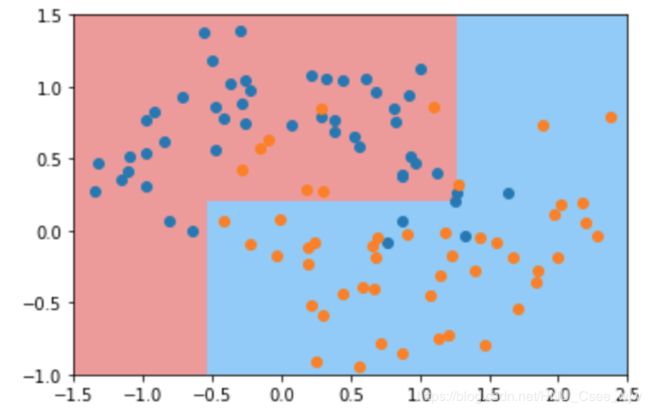
plot_decision_boundary(dt_clf2, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
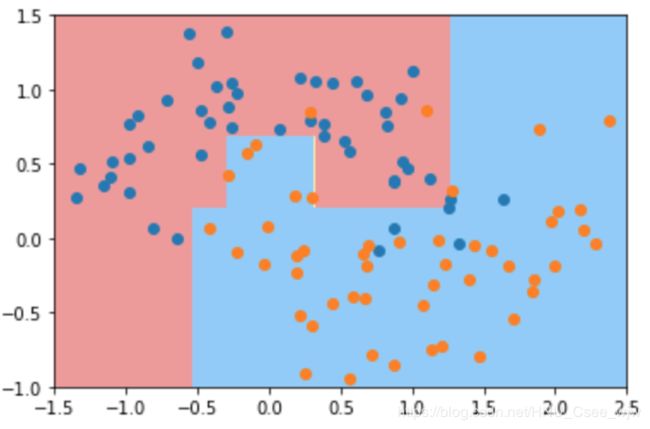
plt.show()dt_clf3 = DecisionTreeClassifier(min_samples_split=10) # 对于一个节点来说,只要有多少个样本数据才对其继续拆分
dt_clf3.fit(X, y)
plot_decision_boundary(dt_clf3, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()dt_clf4 = DecisionTreeClassifier(min_samples_leaf=6) # 对于一个叶子节点,最小应该有几个样本
dt_clf4.fit(X, y)
plot_decision_boundary(dt_clf4, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
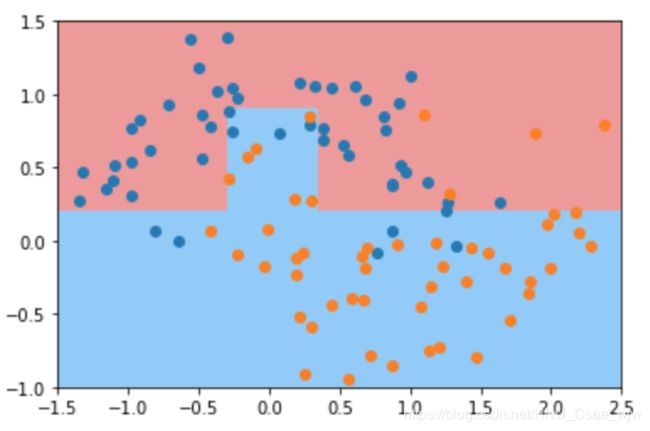
plt.show()dt_clf5 = DecisionTreeClassifier(max_leaf_nodes=4) # 决策树最多有多少个叶子节点
dt_clf5.fit(X, y)
plot_decision_boundary(dt_clf5, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
06 决策树解决回归问题
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)Decision Tree Regressor
from sklearn.tree import DecisionTreeRegressor
dt_reg = DecisionTreeRegressor()
dt_reg.fit(X_train, y_train)
"""
Out[4]:
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
"""
dt_reg.score(X_test, y_test)
# Out[5]:
# 0.58830200768338436
dt_reg.score(X_train, y_train) # 对训练集回归完全正确而测试集表现不好,说明过拟合
# Out[6]:
# 1.007 并查集的局限性
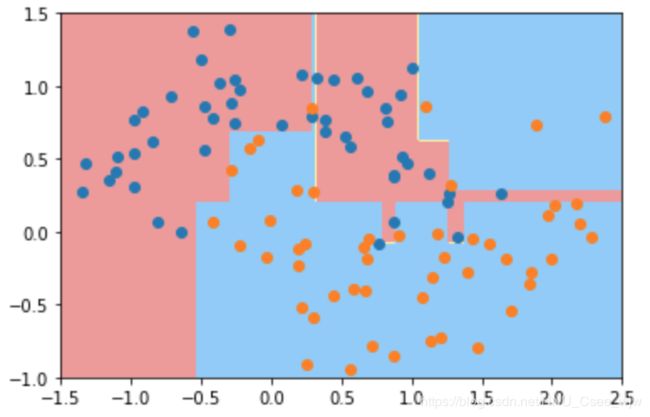
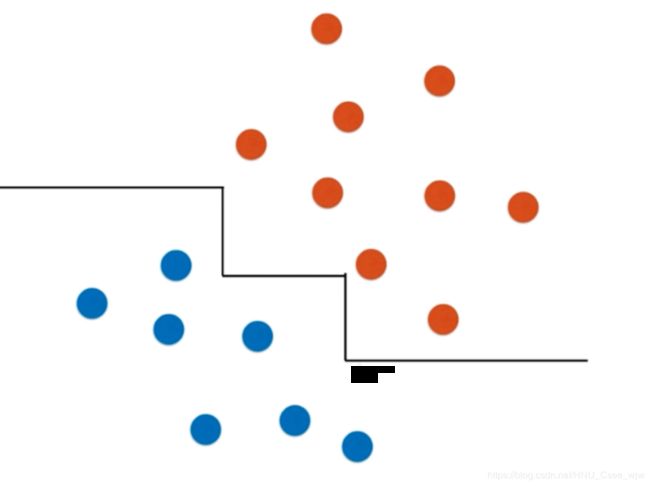
决策树的分类边界和理想的(斜线)有一定的差距
上图决策树绘制出的决策边界可能是错误的,尤其是在x,y接近无穷时的边界部分
缺点2:对个别样本点特别敏感,仿真如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target
from sklearn.tree import DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(max_depth=2, criterion='entropy')
tree_clf.fit(X, y)
"""
Out[3]:
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
"""
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(tree_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
# 删除第138行数据
X_new = np.delete(X, 137, axis=0)
y_new = np.delete(y, 137)
X_new.shape
# Out[7]:
# (149, 2)
y_new.shape
# Out[8]:
# (149,)
tree_clf2 = DecisionTreeClassifier(max_depth=2, criterion='entropy')
tree_clf2.fit(X_new, y_new)
"""
Out[9]:
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')
"""
plot_decision_boundary(tree_clf2, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
最后,如果有什么疑问,欢迎和我微信交流。