简易频率特性测试仪

简易频率特性测试仪

一、项目简介

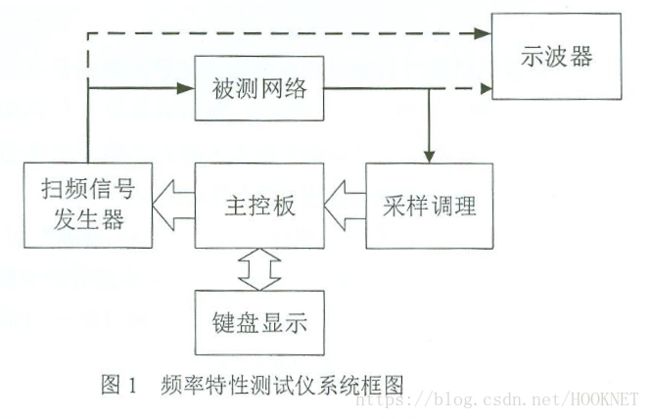
本题是2016年TI邀请赛题目，其原型是2013年国赛E题。本题要求制作设计并制作一台频率特性测试仪，用于测量并显示“被测网络”的频率特性，系统组成框图如图1所示。其原理是基于零中频正交解调原理，其实现方式采用基于FPGA的纯数字结构。

二、系统框图

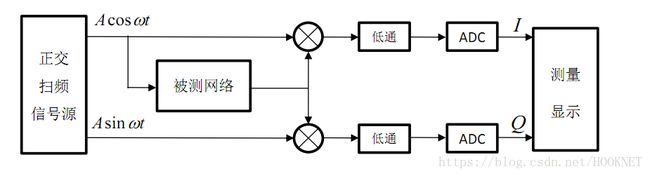
上图为零中频正交解调原理的实现框图。其中，“被测网络”部分由模拟实现，“测量显示”由单片机实现，其余功能均由FPGA实现。

FPGA产生两路正交扫频信号源，其中余弦信号为：

Acosωt A cos ⁡ ω t

通过DA输出到被测网络，经过被测网络后输出为：

Bcos(ωt+ϕ) B cos ⁡ ( ω t + ϕ )

此信号通过AD采集到FPGA内部,分别与两路正交信号相乘，得到同向分量i和正交分量q：

i=Acosωt×Bcos(ωt+ϕ)=A⋅B2[cos(2ωt+ϕ)+cosϕ] i = A cos ⁡ ω t × B cos ⁡ ( ω t + ϕ ) = A ⋅ B 2 [ cos ⁡ ( 2 ω t + ϕ ) + cos ⁡ ϕ ]

q=Asinωt×Bcos(ωt+ϕ)=A⋅B2[sin(2ωt+ϕ)−sinϕ] q = A sin ⁡ ω t × B cos ⁡ ( ω t + ϕ ) = A ⋅ B 2 [ sin ⁡ ( 2 ω t + ϕ ) − sin ⁡ ϕ ]

积化和差公式：

sinα×sinβ=12[cos(α−β)−cos(α+β)]; sin ⁡ α × sin ⁡ β = 1 2 [ cos ⁡ ( α − β ) − cos ⁡ ( α + β ) ] ;

cosα×cosβ=12[cos(α−β)+cos(α+β)]; cos ⁡ α × cos ⁡ β = 1 2 [ cos ⁡ ( α − β ) + cos ⁡ ( α + β ) ] ;

sinα×cosβ=12[sin(α+β)+sin(α−β)]; sin ⁡ α × cos ⁡ β = 1 2 [ sin ⁡ ( α + β ) + sin ⁡ ( α − β ) ] ;

cosα×sinβ=12[sin(α+β)−sin(α−β)]; cos ⁡ α × sin ⁡ β = 1 2 [ sin ⁡ ( α + β ) − sin ⁡ ( α − β ) ] ;

两路信号经过低通滤波器后，高频分量被滤除，得到两路直流分量，假设滤波器的幅度增益为C，则I、Q两路信号分别为：

I=A⋅B⋅C2cosϕ I = A ⋅ B ⋅ C 2 cos ⁡ ϕ

Q=−A⋅B⋅C2sinϕ Q = − A ⋅ B ⋅ C 2 sin ⁡ ϕ

由两路直流分量可得到被测网络的幅度 V V 和相位 ϕ ϕ 两个参数：

V=2(I2+Q2)−−−−−−−−−√A⋅C V = 2 ( I 2 + Q 2 ) A ⋅ C

ϕ=arctan(−QI) ϕ = arctan ⁡ ( − Q I )

由这两个参数便可以绘制出被测网络的幅频和相频特性曲线。

三、各部分设计

1. 模拟部分设计

模拟部分要求制作一个被测网络。该被测网络是一个带通滤波器，由截止频率50k的高通和截止频率300k的低通串联而成。输入输出阻抗都是50欧，且通带电压增益为1，截止频率处衰减相对误差不超过5%。

2. FPGA部分设计

本项目是通过FPGA实现全数字的零中频正交解调。数字部分主要包括以下几个模块：扫频信号源、乘法器、低通滤波器、ADDA等。

输入信号

• 扫频信号源

在FPGA上用DDS产生两路正交扫频信号，扫频范围为10kHz~4MHz,单片机通过串口发送频率控制字来控制正交信号的输出频率。频率控制字的计算公式如下：

Freq_word = Freq * clk / 2^n

其中，“Freq”是输出信号的频率；“clk”是DDS工作时钟；“2^n”是相位累加器位宽，一般为2^32。

• 乘法器

直接调用IP核实现乘法运算，输入数据位宽都为12位，相乘后，输出数据为24位。

• FIR滤波器

低通滤波器是为了滤除高频分量。通过Matlab的FilterDesigner工具，设计出满足要求的滤波器，导出抽头系数文件。在Vivado中调用FIR IP核，导入系数文件，例化模块。

那么如何设计满足要求的滤波器？

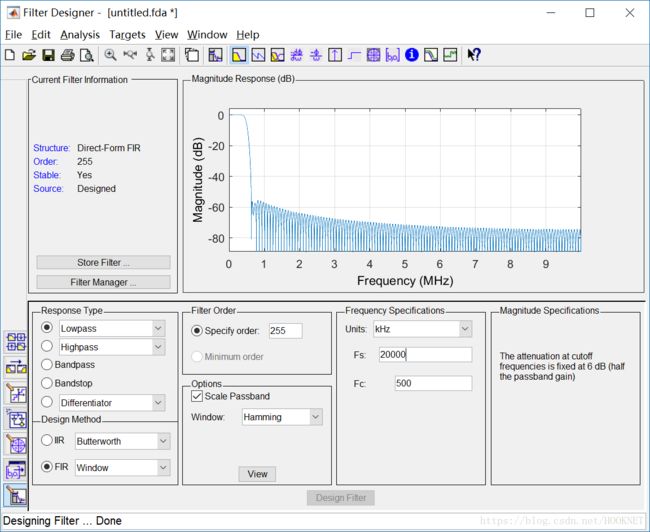
在FilterDesigner中输入滤波器参数，首先是选择窗函数的低通滤波器,窗函数的种类是“Hamming”窗。下面比较重要的是确定采样率和截止频率，以及滤波器的阶数。

题目中要求，扫频范围是10kHz~4MHz，那么经过乘法器之后的信号频率范围是20KHz~8MHz，因此采样率Fc在满足奈奎斯特采样定理的条件下必须高于16MHz，但这时想要滤除20KHz的信号，截止频率Fs就要设的很低，这样的滤波器很难满足要求，除非阶数非常大，而阶数受资源限制。

很明显，-3dB点的频率和10KHz差的很远，不满足设计要求。

对于这种情况，我们似乎需要的是一种截止频率可变的滤波器，能根据信号源的频率改变截止频率。那么如何实现？很简单，在数字滤波器的世界里，滤波都是以数字角频率 ω ω 的形式进行的，一般为了方便才直接说频率 f f 的。角频率与频率存在如下关系：

ω=2⋅π⋅ffs ω = 2 ⋅ π ⋅ f f s

其中 ω ω 是数字角频率； f f 是信号频率； fs f s 是采样频率。

那么对应到截止角频率 ωc ω c 就有如下公式：

ωc=2⋅π⋅fcfs ω c = 2 ⋅ π ⋅ f c f s

其中， ωc ω c 是数字角频率； fc f c 是截止频率； fs f s 是采样率。

从公式中就可以看到，当截止频率和采样率的比值不变时，截止角频率也不会改变。因此，可以通过改变FIR滤波器的采样率，来改变截止频率。首先确定两者比值为40时，幅频特性满足要求。

具体采样率可以按如下方式划分：

信号源频率	乘法器输出频率	截止频率	采样率
10K	20K	10k	400K
50K	100K	50K	2M
250K	500K	250K	10M
1.25M	2.5M	1.25M	50M
4M	8M	1.25M	50M

生成抽头系数之前，还要对系数进行量化，一般量化位宽选择16位或者18位。同时，Matlab还会给出输出数据的位宽，方便在截位时确定输出大小。

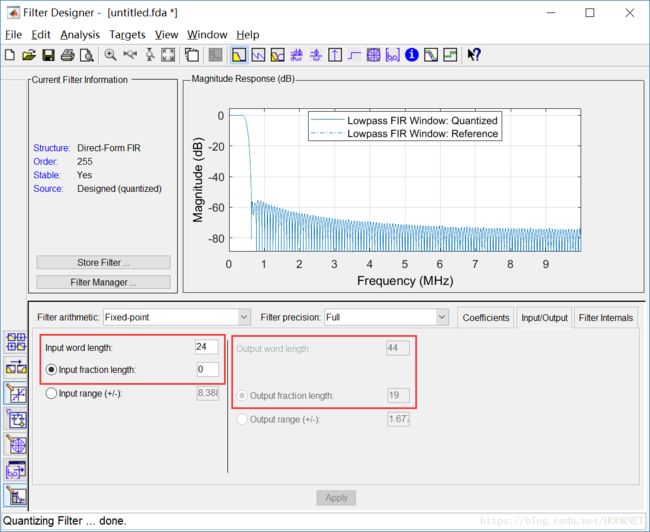
上图中输出数据可以取[44:19]

3. 单片机部分设计