山东大学机器学习(实验二解读)——逻辑回归和牛顿法
1.梯度下降法
x = load('ex2x.dat');
y = load('ex2y.dat');
m = length(y);
xx = x;
mu = mean(x);
sigma = std(x);
x = (x - mean(x))./std(x); %数据标准化
x = [ones(m,1),x] ; xx = [ones(m,1),xx] ;
% find返回满足指定条件的行的索引
pos = find ( y == 1 ) ; neg = find ( y == 0 );
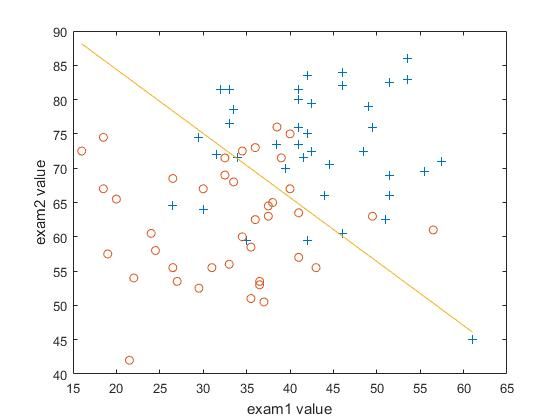
plot (xx( pos , 2 ),xx( pos , 3 ),'+');
hold on;
plot (xx( neg , 2 ),xx( neg , 3 ),'o');
xlabel('exam1 value');
ylabel('exam2 value');
MaxIter = 1500;
theta = zeros(size(x(1,:)))'; %初始化theta
e = 1e-6;
alpha = 0.08;
g = @(z) 1./(1+exp(-z)); %定义sigmoid函数
for i = 1:MaxIter
z = x * theta;
h = g(z); %逻辑回归模型
L_theta(i,1) = -(1/m)*sum(y.*log(h)+(1-y).*log(1-h)); %极大对数似然函数
delta_L = (1/m)*x'*(h-y); %计算梯度
%更新 L 和 theta
if (i > 1) && (abs(L_theta(i,1) - L_theta(i-1,1)) <= e)
break;
end
theta = theta - alpha*delta_L;
store(i,:) = [theta',L_theta(i,1)];
end
%画出决策边界,因为数据是标准化后的,因此需要还原回去
x_axis = x(:,2)*sigma(1) + mu(1);
y_axis = (-theta(1,1).*x(:,1) - theta(2,1).*x(:,2))/theta(3,1);
y_axis = y_axis*sigma(2) + mu(2);
plot(x_axis, y_axis,'-');
figure;
plot(1:i-1,store,'-');
legend('\theta_0','\theta_1','\theta_2','L{(\theta)}');
xlabel('iter value');
ylabel('value');
- 假设 ϵ = 1 0 − 6 \epsilon = 10 ^ { - 6 } ϵ=10−6。实现收很慢敛需要多少次迭代?注意,梯度下降算法收敛速度,可能需要很长时间才能达到最小值。
答:610次
- 收敛后得到的 θ \theta θ值是多少?
θ 0 = − 0.0506 , θ 1 = 1.4305 , θ 2 = 1.5267 \theta_0 = -0.0506, \ \theta_1 = 1.4305,\ \theta_2 =1.5267 θ0=−0.0506, θ1=1.4305, θ2=1.5267
- 计算每次迭代过程中的 L ( θ ) L(\theta) L(θ)和说明 L ( θ ) L(\theta) L(θ)在梯度下降算法中如何减少。
- 收敛之后,使用 θ \theta θ的值找出分类问题的决策边界。
- 测试1的成绩为20分和测试2为80分的学生不被录取的概率是多少?
不被录取的概率为
P ( y = 0 ∣ x ; θ ) = 1 − h θ = 1 − g ( θ T x ) = g ( − θ T x ) P(y=0|x;\theta) = 1 - h_\theta = 1 - g(\theta^Tx) = g(-\theta^Tx) P(y=0∣x;θ)=1−hθ=1−g(θTx)=g(−θTx)
先对 x 1 = 20 , x 2 = 80 x_1=20,\ x_2 = 80 x1=20, x2=80进行标准化
x 1 = ( x 1 − mu(1)) / sigma(1) = − 1.7998 , x 2 = ( x 2 − mu(2)) / sigma(2) = 1.2767 x_1=(x_1 - \text{mu(1))}/\text{sigma(1)}=-1.7998,\quad x_2=(x_2 - \text{mu(2))}/\text{sigma(2)}=1.2767 x1=(x1−mu(1))/sigma(1)=−1.7998,x2=(x2−mu(2))/sigma(2)=1.2767
θ T x = − 0.0506 + 1.4305 × ( − 1.7988 ) + 1.5267 × 1.2767 = − 0.6746 \theta^T x = −0.0506+1.4305×(−1.7988)+1.5267×1.2767=−0.6746 θTx=−0.0506+1.4305×(−1.7988)+1.5267×1.2767=−0.6746
最终得到成绩1为20成绩2为80不被录取的概率为
g ( 0.6746 ) = 1 / ( 1 + exp ( − 0.6746 ) ) = 0.6625 g(0.6746) = 1/(1+\exp(-0.6746)) = 0.6625 g(0.6746)=1/(1+exp(−0.6746))=0.6625
2. 牛顿法
x = load('ex2x.dat');
y = load('ex2y.dat');
m = length(y);
mu = mean(x);
xx = x;
sigma = std(x);
x = (x - mean(x))./std(x);
x = [ones(m,1),x] ;
n = size(x,2);
% find返回满足指定条件的行的索引
pos = find ( y == 1 ) ; neg = find ( y == 0 ) ;
plot ( xx ( pos , 1 ) , xx ( pos , 2 ) , '+' ) ;
hold on
plot ( xx ( neg , 1 ) , xx ( neg , 2 ) , ' o ' )
xlabel('exam1 value');
ylabel('exam2 value');
MaxIter = 1500;
theta = zeros(size(x(1,:)))';
e = 1e-6;
H = zeros(n,n);
g = @(x) 1./(1+exp(-x));
for i = 1:MaxIter
z = x * theta;
h = g(z); %logistic model
L_theta(i,1) = -(1/m)*sum(y.*log(h)+(1-y).*log(1-h)); %log likelihood function
delta_L = (1/m)*x'*(h-y); %calculate gradient
%calculate Hessian matrix
H = (1/m).*x' * diag(h) * diag(1-h) * x;
%update L and theta
if (i > 1) && (abs(L_theta(i,1) - L_theta(i-1,1)) <= e )
break;
end
theta = theta - H^(-1)*delta_L;
store(i,:) = [theta',L_theta(i,1)];
end
x_axis = x(:,2)*sigma(1) + mu(1);
y_axis = (-theta(1,1).*x(:,1) - theta(2,1).*x(:,2))/theta(3,1);
y_axis = y_axis*sigma(2) + mu(2);
plot(x_axis, y_axis,'-');
figure
plot(1:i-1,store,'-');
legend('\theta_0','\theta_1','\theta_2','L{(\theta)}');
xlabel('iter value');
ylabel('value');
- 当收敛时 θ \theta θ的值是多少?
θ 0 = − 0.0566 , θ 1 = 1.4720 , θ 2 = 1.5706 \theta_0 = -0.0566, \ \theta_1 = 1.4720,\ \theta_2 =1.5706 θ0=−0.0566, θ1=1.4720, θ2=1.5706
- 显示牛顿法中 L L L是如何减少的?
- 画出决策边界
- 测试1的成绩为20分和测试2为80分的学生不被录取的概率是多少?
不被录取的概率为
P ( y = 0 ∣ x ; θ ) = 1 − h θ = 1 − g ( θ T x ) = g ( − θ T x ) P(y=0|x;\theta) = 1 - h_\theta = 1 - g(\theta^Tx) = g(-\theta^Tx) P(y=0∣x;θ)=1−hθ=1−g(θTx)=g(−θTx)
先对 x 1 = 20 , x 2 = 80 x_1=20,\ x_2 = 80 x1=20, x2=80进行标准化
x 1 = ( x 1 − mu(1)) / sigma(1) = − 1.7998 , x 2 = ( x 2 − mu(2)) / sigma(2) = 1.2767 x_1=(x_1 - \text{mu(1))}/\text{sigma(1)}=-1.7998,\quad x_2=(x_2 - \text{mu(2))}/\text{sigma(2)}=1.2767 x1=(x1−mu(1))/sigma(1)=−1.7998,x2=(x2−mu(2))/sigma(2)=1.2767
θ T x = − 0.0566 + 1.4720 × ( − 1.7988 ) + 1.5706 × 1.2767 = − 0.6993 \theta^T x = −0.0566+1.4720×(−1.7988)+1.5706×1.2767=−0.6993 θTx=−0.0566+1.4720×(−1.7988)+1.5706×1.2767=−0.6993
最终得到成绩1为20成绩2为80不被录取的概率为
g ( 0.6746 ) = 1 / ( 1 + exp ( − 0.6993 ) ) = 0.6680 g(0.6746) = 1/(1+\exp(-0.6993)) = 0.6680 g(0.6746)=1/(1+exp(−0.6993))=0.6680
- 对比梯度下降法和牛顿法,你学到了什么?
(1)牛顿法:是通过求解目标函数的一阶导数为0时的参数,进而求出目标函数最小值时的参数。
优点:收敛速度很快,而且不需要知道学习率。
海森矩阵的逆在迭代过程中不断减小,可以起到逐步减小步长的效果。
缺点:海森矩阵的逆计算复杂,代价比较大,因此有了拟牛顿法。
(2)梯度下降法:是通过梯度方向和步长,直接求解目标函数的最小值时的参数。
越接近最优值时,步长应该不断减小,否则会在最优值附近来回震荡。
优点:计算简单,实现容易。
缺点:收敛速度比较慢,数据量大还会导致内存不足。