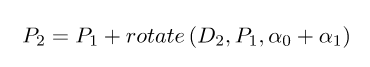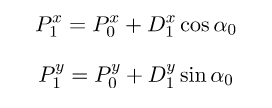程序性动画 2 ——正向运动学的数学运算
本教程将开始逆向运动学世界的旅程。有无数的方式能着手处理这个问题,但它们全都是从正向运动学开始的。
逆向运动学是从空间中取点,并告诉你怎样移动你的胳膊去接触到它。正向运动学解决的方式正好相反。已知你移动手臂的方式,它再告诉你要去够哪个点。
机械手臂 #
逆向运动学最初被用于控制机械手臂。因此,教程将做出假设并使用和机器人相关的用辞。然而,这并不会限制逆向运动学可能涉及的应用领域。无机械模型场景,像是人类手臂、蜘蛛腿还有触手,也都适用。
首先,让我们展示一下“机械手臂”这个术语是什么意思:
上面的图片展示了一个典型的机械手臂,由“ limbs(肢干)”制作,用“ joints(关节)”连接。图片上的机械手臂有了五个独立的关节,就被称为有了五个自由度。每个关节被一个允许移动链条到目标角度的 motor(发动机)控制。
总而言之,我们可以画出关节的精确图表。在这个特制教程中,我们会假设每个关节仅在单一轴向上旋转。
附加在机械手臂末端的工具被称为end effector(末梢执行器)。根据上下文,它可以作为一个自由度参与其中或者不加参与。在这个教程中,我们仅会关注接触动作,那么end effector将不会被考虑到。
正向运动学 #
在这个小装饰品的例子中,每个关节都能在一个特定的轴向上旋转。每个关节的状态因此被当做一个角度来测量。我们通过将每个关节旋转到特定的角度,导致 end effector 到达空间上不同的点。已知 end effector 的位置,给出关节所需旋转的角度,被称为正向运动学。
(译者小妞牛在这里解释一下:end effector 的位置和关节旋转角度共同组成了手臂的移动方式,这是先决条件,然后再由开发者指定移动的目标点,叫做正向运动学。可以和文章开头的释义呼应上,与逆向运动学相反。)
正向运动学是个 “easy” 问题。这意味着每个角度的设置,都有且仅有一个能用精确方式计算出来的结果。了解机械手臂是怎样依靠我们提供给它的 motor 输入来移动的,是我们找到逆向运动学对偶问题解决方案的必要步骤。
几何解释 #
在写代码之前,我们需要明白正向运动学背后的数学概念。甚至在这之前,我们还需要明白什么叫空间几何。
既然在 3D 中显示旋转并不是那么容易,就让我们从位于 2D 空间中的简易机械手臂开始吧。一个机械手臂有自己的“静止位置”,这是模型所有关节回归 “0角度” 时的姿态。
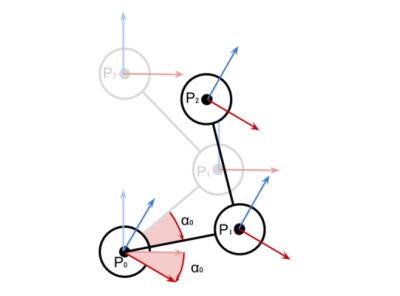
上面的图表展示了带着三个自由度的机械手臂。每个关节旋转到它的 0 度,导致了这个初始姿态。我们能看见通过将第一个关节 p0 旋转 a0 度时,这个姿态是怎样变化的。这导致整个关节链以 p0 作为锚点相应移动。
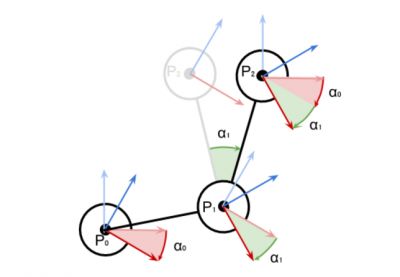
意识到 motor 上附加的其他关节没有移动很重要。每个关节都有助于它前面连接链的本地旋转。下面的图表展现了当第二个关节旋转了 a1 度时,整个模型的姿态是怎么变化的。
当只有 a0 决定 p1 的位置时,p2 才受 a0 和 a1 共同的影响。旋转的参照标准(红色和蓝色箭头)依据更早连接的连接链旋转的总和来调整。
数学部分 #
从先前的图表中我们应该很清楚的解决了正向运动学的问题。我们需要能计算由于旋转它们导致的嵌套物的位置。
让我们看看两个关节是怎样被计算的。一旦解决了这种两个关节的问题,我们就能依次复制来解决任意长度的链条。
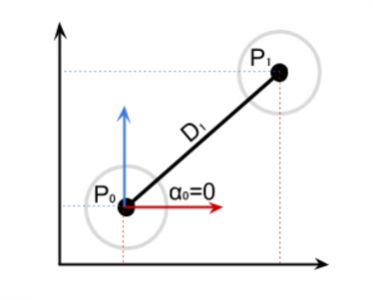
先让们从简单的开始,第一个关节在起始位置,意味着a0 = 0,如下图:
简单说,就相当于:
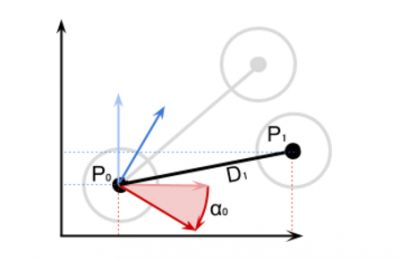
当 a0 不是 0 时,我们必须绕着 p0 将距离向量 D1 旋转 a0 度:
数学上我们可以写成:
之后我们会明白怎样在不搞乱三角形的前提下使用这个函数。
通过复用相同的逻辑,我们能获得 p2 的方程式:
最终,一般方程式是:
我们会在接下来的教程《执行正向运动学》中,了解方程式是怎样转化为 C# 代码的。
2D 中的正向运动学 #
如果你熟悉 2D 中的旋转,则 2D 中的正向运动学可以由三角法来完成:
想要引出更多信息,你可以阅读 2D 旋转基础入门 (A Gentle Primer on 2D Rotations)。
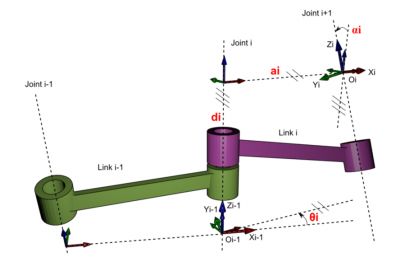
德纳维·哈登伯格矩阵是什么? #
如果你有工程学背景,你可能会有不同的方法来解决这个问题。正反运动学问题十分普遍,还有几个解决问题的标准化方法。方法的其中之一是把每个关节的四个参数联系起来,被称为德纳维·哈登伯格参数。在矩阵中它们易于操作,并且是解决逆向运动学问题的最好办法。
然而此教程并不依赖于此。解决德纳维·哈登伯格矩阵要求的数学知识比大多数程序员愿意做的更多。方法上我们更倾向于梯度下降,这是一种普适性最优化算法。
你可以从这里下载 Unity 项目工程:https://www.patreon.com/posts/8928832
从这里可以下载机械手臂的 3D 模型:https://3dwarehouse.sketchup.com/model/92e064854f4dd504c8ab9067fbd9681d/Robotic-Arm-stainless-steel-R6Stainless
原文作者:Alan Zucconi
原文链接:http://www.alanzucconi.com/2017/04/06/forward-kinematics/
End.