JAVA:基本排序算法
本章代码地址:https://github.com/hustuhao/SortAlgorithm
目录
1,逆序排序
2,选择排序
3,冒泡排序
4,折半查找
5,快速排序(quickSort)
6,归并排序
7,希尔排序(Shell Sort)
8,桶排序(Bucket Sort)
9,基数排序
10,插入排序
11,堆排序
1,逆序排序
将有序数组逆序排序。
例如:对{1,2,3,4,5,6} 数组逆序排序:{6,5,4,3,2,1}
public static void reverse(int[] arr){
//利用循环,实现数组遍历,遍历过程中,最远端换位
//for的第一项,定义2个变量, 最后,两个变量++ --
for( int min = 0 , max = arr.length-1 ; min < max ; min++,max--){
//对数组中的元素,进行位置交换
//min索引和max索引的元素交换
//定义变量,保存min索引
int temp = arr[min];
//max索引上的元素,赋值给min索引
arr[min] = arr[max];
//临时变量,保存的数据,赋值到max索引上
arr[max] = temp;
}
}2,选择排序
<选择排序>内容引用自《我的第一本算法书》第二章第三节
选择排序就是重复“从待排序的数据中寻找最小值,将其与序列最左边的数字进行交换”这一操作的算法。在序列中寻找最小值时使用的是线性查找。
时间复杂度分析:主要的操作就是查找待排序序列中的最小值,因此采用的查询算法决定了选择排序的复杂度。
这里使用线性查找,寻找最小值(要寻找n-1次最小值)。所以整个选择排序的时间复杂度为 ![]()
例如:对数组{6,1,7,8,9,3,5,4,2}进行选择排序
原序列:
第一轮选择排序:
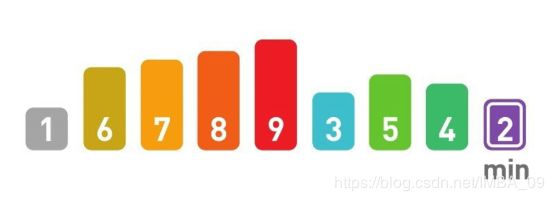
找到最小的数1:
将1放到已排序数组的最右边(灰色部分):
第二轮选择排序:
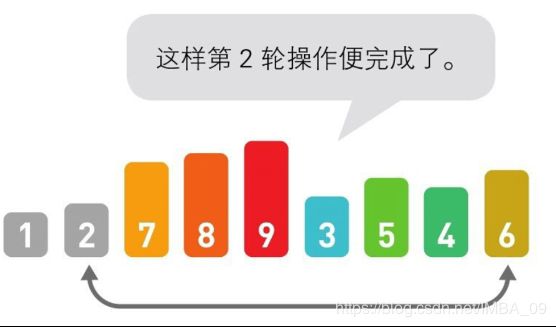
找到待排序序列中的最小值2:
将最小值2放到已排序序列的最右边(灰色部分)
剩下的排序过程也按照上述进行。
算法实现:
public void SelectionSort(int arr[]){
for(int i = 0 ; i < arr.length - 1; i++){ //内循环,是每次都在减少,修改变量的定义
int min = i;
for(int j = i+1 ; j < arr.length ; j++){ //数组的元素进行判断
if(arr[min] > arr[j]){ //数组的换位
min = j;
}
}
//将待排序序列的最小值放到i处
swap(arr,min,i);
}
}3,冒泡排序
定义:冒泡排序就是重复“从序列一边开始比较相邻两个数字的大小,再根据结果交换两个数字的位置”
每一轮操作的目的就是选出最小(或者最大)的元素,排到序列的一边。
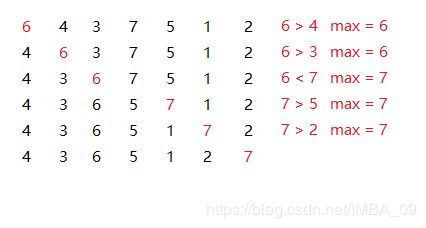
举例:对 序列{6,4,3,7,5,1,2}进行冒泡排序(最大的选到右边),
第一轮过程如下图:
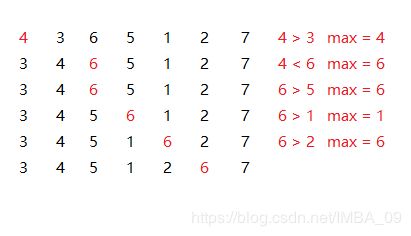
第二轮过程如下图:(与上面的操作完全相同)
不用比较6和7,7是上一轮选出来的最大的数,6是本轮选出来的第二大的数。
时间复杂度:
第一轮要比较n-1次
第二轮要比较n-2次
因此总比较次数为:(n-1)+(n-2)+....+1 = n(n-1)/2,其与输入数据的排序无关,是定值。
但是交换的次数和输入数据的排序有关:
两种极端的情况,序列是从小到大排序(时间复杂度0)和从大到小排序(时间复杂度O(n^2))
算法实现:
注意:
进行 (arr.leng-1)轮“冒泡操作”:每一轮选出未排序中的最大数。
这里arr[0]最小,arr[arr.length-1]最大。每一轮结束后,未排序的数都减少了一个,所以内层循环的次数为arr.length-i-1。
public static void bubbleSort(int[] arr){
for(int i = 0 ; i < arr.length - 1; i++){ //每次内循环的比较,从0索引开始, 每次都在递减
for(int j = 0 ; j < arr.length-i-1; j++){ //比较的索引,是j和j+1
if(arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}4,折半查找
折半查找法,又名二分查找法
实现步骤:
1. 需要的变量定义
三个,三个指针
2. 进行循环折半
可以折半的条件 min <= max
3. 让被找元素,和中间索引元素进行比较
元素 > 中间索引 小指针= 中间+1
元素 < 中间索引 大指针= 中间-1
元素 == 中间索引 找到了,结束了,返回中间索引
4. 循环结束,无法折半
元素没有找到 ,返回-1
/*
定义方法,实现,折半查找
返回值: 索引
参数: 数组,被找的元素
*/
public class int binarySearch(int[] arry, int key){
int min = 0;
int max = arr.length - 1;
int mid = 0;
while(min <= max){
mid = (min + max)/2;
if(key > arr[mid]) {
min = mid + 1;
}else if(key < arr[mid]){
max = mid - 1;
}else{
return mid;
}
}
return -1;
}5,快速排序(quickSort)
快速排序(Quicksort)是对冒泡排序的一种改进。
基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序(称为子问题),整个排序过程可以递归进行,以此达到整个数据变成有序有序序列。
解决子问题的时候,仍然要使用快速排序,只有子问题只剩一个数字的时候,排序才算完成
(分而治之)
算法的实现 1:
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据(key),然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。注意:快速排序不是一种稳定的排序算法,即多个相同的值的相对位置也许会在算法结束时产生变动。
一趟快速排序的算法是:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于key的值A[j],将A[j]和A[i]互换,执行第四步。
4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]互换;执行第五步。
5)重复第3、4步,直到i=j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。另外,i==j ( 此时的位置就是 key 所在的位置 )这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
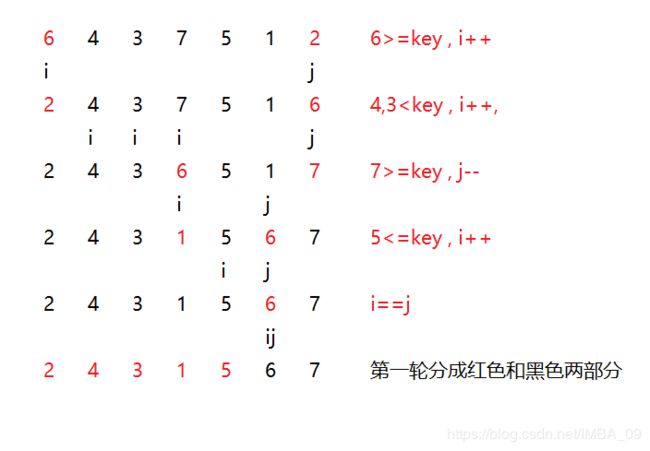
举例:对{6,4,3,7,5,1,2}进行快速排序
第一轮快速排序如下:
接下来就是对{2,4,3,1,5} 和{6,7}分别进行快速排序。
public static void quickSortA(int[] arr,int low,int high){
int i=low;
int j=high;
int key=arr[low];
//本轮结束条件 i==j
while(i=key) j--;
//交换a[i]和a[j]
if(i key
while(ilow)quickSortA(arr,low,i-1);
if(j 非递归实现 :
public void quickSort(int[] arr){
int low = 0;
int high = arr.length - 1;
LinkedList queue = new LinkedList();
queue.offer(low); //存储区间 [low,high]
queue.offer(high);
while(!queue.isEmpty()){ //使用队列来存储区间信息
low = queue.poll();
high = queue.poll();
int i = low ,j = high;
int key = arr[low];
//本轮结束条件 i==j
while(i=key) j--;
//交换a[i]和a[j]
if(i key
while(ilow){
queue.offer(low); // 存区间[low,i-1]
queue.offer(i-1);
}
if(j
时间复杂度:
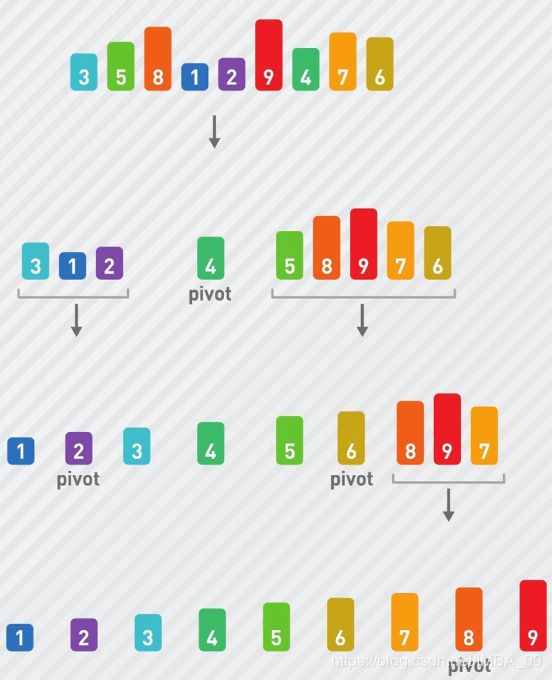
分割子序列时需要选择基准值,如果每次选择的基准值都能使得两个子序列的长度为原本的一半,那么快速排序的运行时间和归并排序的一样,都为O(nlogn)。和归并排序类似,将序列对半分割log2n次之后,子序列里便只剩下一个数据,这时子序列的排序也就完成了。因此,如果像下图这样一行行地展现根据基准值分割序列的过程,那么总共会有log2n行。
<参考<我的第一本算法书>>
算法实现2:参考《我的第一本算法书》
第一步:选择基准(privot):首先任意选取一个数据(通常选用数组的第一个数)作为关键数据(key)
第二步:设置两个变量i、j,排序开始的时候:i=0,j=N-1;从前到后比较序列中的数与key的大小,小的放在前面(i++),大的放在后面(j--),直到i==j,这就是第一轮快速排序。
第三步:将上一步的序列分成(low,i-1) 和 (i+1,high) 将序列以key为界分成大于key和小于key的两部分:不把key放入其中。
第四步:分别对第三步的两个序列进行第一步和第二步操作。
总结:
快速排序的实现原理很简单,就是将原数组分成两部分,然后以中间值为标准,比它小的就放其左边,比它大的就放其右边,然后在左右两边又以相同的方式继续排序。
算法实现:首先要创建两个移动的变量,一个从最左边开始往右移动,一个从最右边开始往左移动,通过这两个变量来遍历左右两部分的元素。当发现左边有大于中间数的元素,右边有小于中间数的元素,此时就进行交换。当两个变量重合也就是相等的时候遍历结束,然后左右两部分作递归处理。
6,归并排序
英文名:Merge Sort,Java 1.8 中的Arrays 和 Collections工具类中的自然排序就是使用的归并排序。
基本思想:该算法将序列分成长度相同的两个子序列,当无法继续往下分时,(即每一个子序列中只有一个元素的时候),就对子序列进行归并(将两个排序好的子序列合并成一个有序序列),该操作会一直重复执行,知道所有的子序列都归为一个整体。
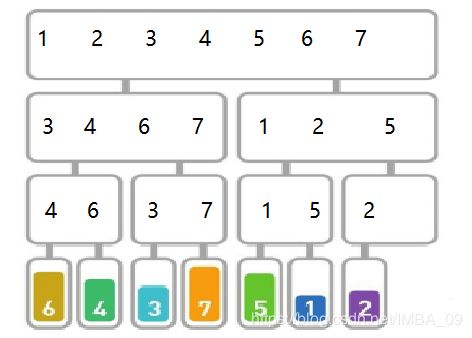
举例说明:对序列{6,4,3,7,5,1,2}进行归并排序
步骤一:将序列分为两半:{6,4,3,7} 和 {5,1,2}
步骤二:继续分:{6,4} {3,7} 和 {5,1} {2}
步骤三:{2}中只有一个元素,所以不继续分。继续分剩下的:{6}{4} 和 {3}{7} 和 {5}{1} {2}
步骤三:归并:{4,6} 和 {3,7} 和 {1,5}{2}
步骤四:归并有序子序列 A : {4,6} 和 B : {3,7} (将两个有序数组合并)
步骤4.1:比较两个子序列首元素的大小,再移动较小的数字
4>3,把3提到新序列:{3},接下来比较4和7
4<7,把4提交新序列:{3,4},接下来比较6和7
6<7,把6提到新序列:{3,4,6},序列A比较完毕,将序列B中剩下的数字全部加入新的序列。
得到新序列:E {3,4,6,7}
步骤五:归并有序子序列:C{1,5} 和 D{2}
步骤5.1:类比步骤四得到新的子序列:F {1,2,5}
步骤六:归并有序子序列E{3,4,6,7} 和 F{1,2,5}
步骤6.1:比较两个子序列首元素的大小,再移动较小的数字
3>1 {1}
3>2 {1,2}
3<5 {1,2,3}
4<5 {1,2,3,4}
6>5 {1,2,3,4,5}
F序列比较完毕,将E序列的剩下的数全部加入新序列{1,2,3,4,5,6,7}
时间复杂度的计算:分割序列所花费的时间不算在运行时间内(可以当作序列本来就是分割好的)。在合并两个已排好序的子序列时,只需重复比较首位数据的大小,然后移动较小的数据,因此只需花费和两个子序列的长度相应的运行时间。也就是说,完成一行归并所需的运行时间取决于这一行的数据量。[引用自:《我的第一本算法书》]
将长度为n的序列对半分割成直到只有一个元素,可以分成log2(n)行,每一行的运行时间都是O(n),总的运行时间为O(nlogn)
算法实现:
/**
* 这种方法没有实现链表的深拷贝,
* 是对链表上的节点直接进行操作,
* 可以对比一下排序前和排序后的链表的变化
* 用单链表做存储结构
定义链表节点
public class ListNode {
public int val;
public ListNode next = null;
public ListNode() {
}
public ListNode(int val) {
this.val = val;
}
}
*/
public class MergeSortDemo {
public ListNode sortList(ListNode head) {
//采用归并排序
if (head == null || head.next == null) {
return head;
}
//获取中间结点
ListNode mid = getMid(head);
ListNode right = mid.next;
mid.next = null;
//合并
return mergeSort(sortList(head), sortList(right));
}
/**
* 获取链表的中间结点,偶数时取中间第一个
* @param head
* @return
*/
private ListNode getMid(ListNode head) {
if (head == null || head.next == null) {
return head;
}
//快慢指针
ListNode slow = head, quick = head;
//快2步,慢一步
while (quick.next != null && quick.next.next != null) {
slow = slow.next;
quick = quick.next.next;
}
return slow;
}
/**
* 归并两个有序的链表
* @param head1
* @param head2
* @return
*/
private ListNode mergeSort(ListNode head1, ListNode head2) {
ListNode p1 = head1, p2 = head2, head;
//得到头节点的指向
if (head1.val < head2.val) {
head = head1;
p1 = p1.next;
} else {
head = head2;
p2 = p2.next;
}
ListNode p = head;
//比较链表中的值
while (p1 != null && p2 != null) {
if (p1.val <= p2.val) {
p.next = p1;
p1 = p1.next;
p = p.next;
} else {
p.next = p2;
p2 = p2.next;
p = p.next;
}
}
//第二条链表空了
if (p1 != null) {
p.next = p1;
}
//第一条链表空了
if (p2 != null) {
p.next = p2;
}
return head;
}7,希尔排序(Shell Sort)
参考:https://blog.csdn.net/weixin_37818081/article/details/79202115
import org.junit.Test;
/*希尔排序,插入排序的一种改进方法
* 与插入排序的不同之处在于:每一次数组序号不是变化1,而是变化increment
* */
public class ShellSort {
public void shellSort(int[] arr){
int len = arr.length;
int increment = len/3+1;
while(increment >=1){
/*这一段由直接插入排序改编而来
* 新序列:i,i+increment,i+2*increment,...,i+n*increment
* 对这个序列进行直接插入排序
* 一个整个for循环对应一个序列
* */
for(int i=increment;i0;j=j-increment){
//这里j-increment保证数组不越界
if((j-increment)>=0 && arr[j] < arr[j-increment] ) {
swap(arr, j, j-increment);
}else{
break;
}
}
}
if(increment==1)break;//increment=1就是最后一次进行插入排序
increment = increment/3+1;
}
}
/*交换数组中两个元素的位置*/
private void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
/*测试用例*/
@Test
public void testShellSortTest(){
int arr[] = new int[]{12,5,9,36,8,21,7};
int arr2[] = new int[]{6,5,4,3,2,1};
int arr3[] = new int[]{};
int arr4[] = new int[]{0};
int arr5[] = new int[]{1,2,3,4,5,6};
shellSort(arr);
shellSort(arr2);
shellSort(arr3);
shellSort(arr4);
shellSort(arr5);
}
}
8,桶排序(Bucket Sort)
参考 https://blog.csdn.net/u012194956/article/details/79887143
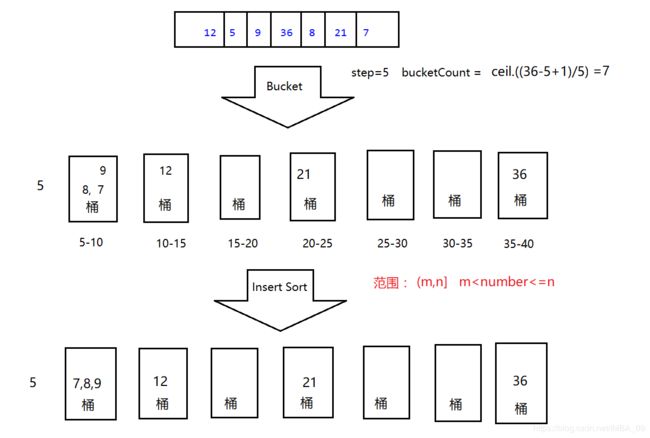
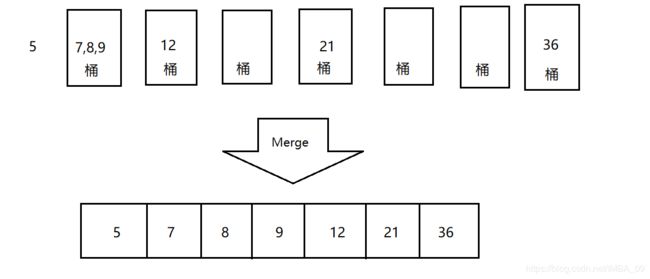
实例:对{12,5,9,36,8,21,7}进行桶排序
然后将桶合并:
9,基数排序
/**
* @param number 待排序的数组
* @param d 最大的位数
* LSD法
*/
public static void radixSortLsd(int[] number,int d){
int k = 0;
int n = 1;
int m = 1; //控制键值排序依据在哪一位
ArrayList[] bucket = new ArrayList[10];
//注意这里要对数组里面的对象初始化,否则会报错:NullPointerException
for(int i=0;i<10;i++){
bucket[i] = new ArrayList();
}
//从个位数开始分类
while(m <= d){
for(int i = 0; i < number.length; i++)
{
int lsd = ((number[i] / n) % 10);
bucket[lsd].add(number[i]);
}
for(int i = 0; i < 10; i++)
{
if(!bucket[i].isEmpty())
for(int j = 0; j < bucket[i].size(); j++)
{
number[k] = bucket[i].get(j);
k++;
}
bucket[i].clear();
}
n *= 10;
k = 0;
m++;
}
} 10,插入排序
插入排序是一种从序列左端开始依次对数据进行排序的算法。在排序过程中,左侧的数据陆续归位,而右侧留下的就是还未被排序的数据。插入排序的思路就是从右侧的未排序区域内取出一个数据,然后将它插入到已排序区域内合适的位置上。
插入排序和选择排序 的区别:
选择排序是选择当前的最小的数插入到已排序数列的最小数的位置,而插入排序是从未排序数列中取一个数,插入到已排序数列的合适位置。他们两者的时间复杂度均为 ![]()
算法实现:
public void insertSort(int[] arr){
int len = arr.length;
if(len<=1)
return;
for(int i=0;i0;j--){
if(arr[j] < arr[j-1]) {
swap(arr, j, j-1);
}else{
break;
}
}
}
}
/*交换数组的两个位置*/
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
} 11,堆排序
堆排序:用来处理 “ 大数据 ” 问题,比如 TopK 问题
实现方法一:堆排序在Java中可以使用“优先队列” ( PriorityQueue ,非线程安全) 来实现。PriorityBlockingQueue ( 线程安全 )
--------- to do ----------
实现方法二:自己构建堆
实现过程:构建最大堆 buildMaxHeap ——>取出最大的元素 ——>调整堆,堆化 heapfy
递归:
public class HeapSort {
/**
*
* @param sourceArray
* @return //注意,最大的那个结点是在数组的末尾
* @throws Exception
*
* 过程:
* 1-将数组变成大顶堆(用数组表示完全二叉树)
* 比如数组:{12,5,9,36,8,21,7}
* 12
* / \
* 5 9
* /\ /\
* 36 8 21 7
* 大顶堆{36,12,21,5,8,9,7}
* 36
* / \
* 12 21
* /\ /\
* 5 8 9 7
*
* 2-将最大的数取出来,将剩下的数组元素重新构建成一个大顶堆。(参考堆的删除数据)
* 3-继续取出大顶堆里面最大的元素(数组的第一个元素),直到剩下堆里面的元素只剩一个
*/
public int[] heapSort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int len = arr.length;
//建立最大堆
buildMaxHeap(arr, len);
//堆排序,将大顶堆变为有序序列
for (int i = len - 1; i > 0; i--) {
//arr[0]从处是最大值,所以把最大值放在最后面。
swap(arr, 0, i);
len--;
// 重建大顶堆
// 将arr变成大顶堆,使arr[0]存储当前大顶堆最大值
heapfy(arr, 0, len);
}
return arr;
}
/**
* 构建大顶堆
*/
private void buildMaxHeap(int[] arr, int len) {
//这里需要理解 len/2 ,详情请复习:完全二叉树的性质
// i/2是求i的父节点,也就是从右往左,从下往上进行堆化
for (int i = len/2 ; i >= 0; i--){
//这里的i都是非叶子结点(0,i)
heapfy(arr, i, len);
}
}
/**
* 将序列转化为堆
* heapify (堆化)
* @param arr
* @param i 某个结点
* @param len
*/
private void heapfy(int[] arr, int i, int len) {
//完全二叉树的性质,left表示该结点左孩子的位置,right表示右孩子的位置
int left = 2 * i + 1;
int right = 2 * i + 2;
//大顶堆,顶点是最大的。
int largest = i;
//开始调整数组,比较左孩子和根结点的大小
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
//比较右孩子和当前根结点的大小
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
// arr[i]的左右孩子中,有比i更大者
if (largest != i) {
swap(arr, i, largest);
heapfy(arr, largest, len);
}
}非递归实现:
修改递归实现中的heapfy
private void heapfy(int[] arr, int i, int len) {
Stack stack = new Stack();
stack.push(i);
while(!stack.isEmpty()){
i = stack.pop();
//完全二叉树的性质,left表示该结点左孩子的位置,right表示右孩子的位置
int left = 2 * i + 1;
int right = 2 * i + 2;
//大顶堆,顶点是最大的。
int largest = i;
//开始调整数组,比较左孩子和根结点的大小
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
//比较右孩子和当前根结点的大小
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
// arr[i]的左右孩子中,有比i更大者
if (largest != i) {
swap(arr, i, largest);
stack.push(largest);
//heapfy(arr, largest, len);
}
}
}