LDA（一）：LDA前身PLSA介绍与推导
PLSA介绍与推导：
概率隐语义分析（PLSA）是一个著名的针对文本建模的模型，是一个生成模型。因为加入了主题模型，所以可以很大程度上改善多词一义和一词多义的问题。
数学基础：
生成模型： 预测模型的公式是 P(y|x) ，即给定输入，输出给定输入的概率分布，就要学习联合分布 P(x,y) ，所以还要先求出 P(x) ，反应的数据本身的相似度。 这样的方法之所以称为生成方法，是因为模型表示了给定输入X产生输出Y的生成关系。用于随机生成的观察值建模，特别是在给定某些隐藏参数情况下。典型的生成模型有：朴素贝叶斯和隐马尔科夫模型等。（但是朴素贝叶斯没有体现词之间的关系！）
而判别模型：没有中间过程，直接对样本学习出概率 P(y|x) ，也可写作 P(y|x；θ) ,可以理解为给定 θ 值的情况下根据特征值来预测概率，想想LR就是这样的。我们只不过要先梯度下降求出 θ 罢了，如svm，LR 对于分类任务常用
生成文档（文本建模）
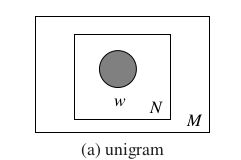
Unigram模型:
这里我们称这个包含不重样单词的集合为词袋（bags of words）
对于Unigram模型，生成一篇文档的方法就是随机的从这个词袋中抽取单词组成。而这篇文档的被生成的概率就是被抽出每个词概率（首发球员）的乘积
所以生成一篇文档 w→=(w1,w2,w3...wn) 的概率就是
假设语料库中有多篇文档，而且文档与文档之间是独立的，那么整个语料库的生成概率就是就是n篇文档概率之积：
2.Mixture of unigrams模型：
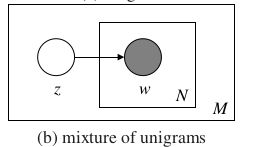
对于Mixture of unigrams，我们在生成一篇文档之前先给它一个主题（注意：这篇文档只有这一个主题），然后根据这个主题的（词袋）词分布来随机选择出n个词
所以对于整个语料库，生成文档的概率就是：对每个主题下生成的文档(每个主题可以随机挑所以可以生成多个文档)的概率进行加和：
3.PLSA模型：
就以上两个模型来说，每个文档只包含一个主题未免太单一了。Hoffmm在1999年提出了概率隐语义分析（Probabilistic Latent Semantic Analysis）。他认为每个主题下都有一个词汇的概率分布，而一篇文章通常由多个主题构成，并且文章中的每个单词都是由某个主题生成的。
每个文档在所有主题上服从多项分布
P z1 z2 … zk 文档 d1 0.3 0.05 … 0.01 文档 d2 0.05 0.2 … 0.05 … … … … … 文档 di 0.01 0.2 … 0.01
每个主题在所有词上服从多项分布。
P w1 w2 … wj 主题 z1 0.1 0.25 … 0.11 主题 z2 0.25 0.1 … 0.15 … … … … … 主题 zk 0.21 0.1 … 0.05
1.所以整篇文档的过程就是：
- 1.先以 p(di) 的概率选中文档 dj
2.以 p(zk|di) 的概率从这个文档 i 的主题概率分布中挑选出主题 zk
3.以 p(wj|zk) 的概率产生一个单词 wj
这其实就是一个简单的单链贝叶斯网络，因为里面包含隐变量 z ，所以通常采用EM算法学习模型参数，所以有如下推导过程。
2.算法推导过程：
- 观察数据为 (di,wj) 对，主题 zj 是隐含变量，对 (di,wj) 进行极大似然估计。
- 目标函数存在未知变量，使用EM算法求最优值。
- E-step:假定参数已知，求 zk 的后验概率。
- M-step:求似然函数期望最大值(实为找到
最优参数)。
- 存在约束条件，转换为拉格朗日乘子法，求驻点 。
- 不断迭代EM步直到收敛。
详细过程如下：
2.1.首先明确两个重要概率：
- (di，wi) 的联合分布（某文档和某个词同时出现的概率）为：
p(di,wj)=p(wj|di)∗p(di)
- 某个文档生成某个词的概率，
而计算每个文档的主题分布是PLSA任务的目标？：p(wj|di)=∑k=1kp(wj|zk)p(zk|di)
- 第一个公式好理解，就是该文档出现的概率乘以该文档下出现该词的概率
- 第二个公式可以理解为有语料库中
某个词的生成概率p(wi) 得来的
- p(wj)=∑kk=1p(wj|zk)p(zk) 这是全概率公式，可理解为每个主题下生成该词概率的加和。
- 我们对上式同时除以一个 di ，得到 p(wj|di)=∑kk=1p(wj|zk,di)p(zk|di) ,
- 在贝叶斯网络中
，这是一个Head to tail模型。 z 将 d ， w 阻隔，在 z 已知的情况下， d 对 w 无影响。所以上式就可以简化成我们的第二个公式 p(wj|di)=∑kk=1p(wj|zk)p(zk|di)
2.2 对观察数据 (di，wi) 进行极大似然估计（目标函数是所有出现概率的乘积）：
L=∏Ni=1∏Mj=1p(di,wj)=∏i∏jp(di,wj)n(di,wj) 这里 n(di,wj) 代表这个文档和词同时出现的次数，类似于二项分布 p3(1−p)2 。另外，因为有重复的出现，出现次数就不是 M 或 N 了，所以不标记。
取对数似然:
l=∑i∑jn(di,wj) log p(di,wj)=∑i∑jn(di,wj) log p(wj|di)p(di) 参照（1）式
=∑i∑jn(di,wj) log[ p(wj|zk)p(zk|di)p(di)] 参照（2）式
=∑i∑jn(di,wj)( log[ p(wj|zk)p(zk|di)]+log p(di))
=∑i∑jn(di,wj) log p(wj|zk)p(zk|di))+∑i∑jn(di,wj)log p(di) 出现的次数是确定的，文档的概率也是已有的，对求取极大值点无影响，所以省略。
由此，我们得到新的目标似然函数：
l=∑i∑jn(di,wj) log p(wj|zk)p(zk|di)
2.3使用逐渐逼近的EM方法：
观察目标函数，其中 p(wj|zk) 和 p(zk|di) 都是未知变量。存在
隐变量z，所以这里我们采用EM算法来估计这两个参数。
- E步(求隐变量后验概率（条件概率）)：为了进行EM算法迭代，我们需要先求出变量的后验分布。所以此处就假定 p(wj|zk) 和 p(zk|di) 已知（因为总会收敛，所以在这里不妨把未知变量随机假定一个值），求出隐含变量Z的后验分布以进行下面的M步。
- M步(求似然函数期望的最大值(似然函数乘以隐变量条件概率))：在 (di,wj,zk) 已知的前提下，求关于参数 p(wj|zk) 和 p(zk|di) 的似然函数期望最大值。得到它们的最优解 p(wj|zk) 和 p(zk|di) ，带入E步，循环迭代。
步骤推导：
2.3.1 zk 的后验概率（隐变量的条件概率）：
- 由贝叶斯公式得到： zk 的后验概率 p(zk|wj)=p(wj|zk)p(zk)∑kk=1p(wj|zk)p(zk)
- 和前面贝叶斯网络一样，同除 di ，而 di 对 wj 是没有影响的，所以可以忽略：
p(zk|di,wj)=p(wj|zk)p(zk|di)∑kk=1p(wj|zk)p(zk|di)
2.3.2求似然函数期望最大值：
回顾EM算法整体框架：
Repeat until convergence{
(E-step) For each i, set
Qi(z(i)):=p(z(i)|x(i);θ) }隐变量的条件概率
(M-step)Set
θ:=arg maxθ∑i∑(i)zQi(z(i))logp(z(i),x(i);θ)Qi(z(i))
- 对于M步，我们可以将他进行简化：
- 这里简略表示 θ:=QlogPQ=Q(logP−logQ)=QlogP−QlogQ≃QlogP 虽然我们求得是最大值，但并不关心具体是多少，而是关注什么参数下取得极大值。那么假如我们已经求出了后验分布Q，成为了已知，对参数估计没有影响，所以 QlogQ 可以省略。
由此我们得到最新的似然函数期望最大值公式：θ:=arg maxθ∑i∑z(i)Qi(z(i))log p(z(i),x(i);θ)
跳出框架，我们把此式应用到前面的目标似然中：
l=∑i∑jn(di,wj) log p(wj|zk)p(zk|di)
=∑i∑jn(di,wj) log p(wj|di)
方便对比M-step，写回原式，这里 log p(wj|di)) 就是包含隐变量 zk 的似然函数 log p(wj,zk|di) ,然后再去乘以隐含变量条件概率求期望。
得到似然函数期望公式：
E(l)=∑i∑jn(di,wj) log p(wj,zk|di)∑k=1kp(zk|di,wj)
E(l)=∑i∑jn(di,wj) log p(wj|zk)p(zk|di)∑k=1kp(zk|di,wj)暴露 p(wj|zk),p(zk|di) 出是因为我们要求关于这两个概率的期望最大值。并且PLSA的核心就是求这两个概率。
注意：这里存在两个约束条件：
有约束条件我们就直接上拉格朗日乘子法：
求驻点：
∂Lag∂p(wj|zk)=∑in(di,wj)p(zk|di,wj)p(wj|zk)−τk=0 当j,k同时存在求驻点时才有 ∑j,∑K 项，所以都被省略掉
∂Lag∂p(zk|di)=∑in(di,wj)p(zk|di,wj)p(zk|di)−ρi=0
分析第一个等式：
∂Lag∂p(wj|zk)=∑in(di,wj)p(zk|di,wj)p(wj|zk)−τk=0 **
⇉∑in(di,wj)p(zk|di,wj)=τk p(wj|zk) (1)
⇉∑i∑Mj=1n(di,wj)p(zk|di,wj)=∑Mj=1τk p(wj|zk) 对第k个主题下所有单词的概率求和 = 1
⇉∑i∑Mj=1n(di,wj)p(zk|di,wj)=τk 其中 p(zk|di,wj) 我们是可以通过E-step求出来的,把 τk 带回到(1)得到：
最终得到M-step：
加上之前的E-step：
不断EM迭代，最终使 p(wj|zk) 和 p(zk|di) 收敛
参考：
【1】邹博-机器学习