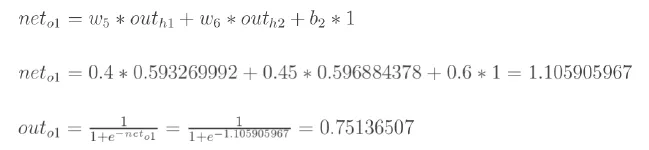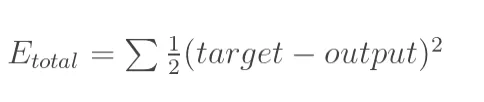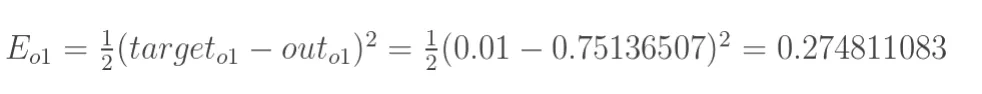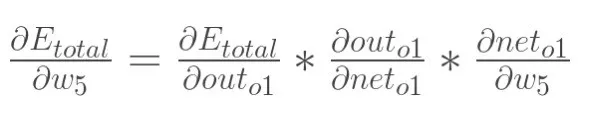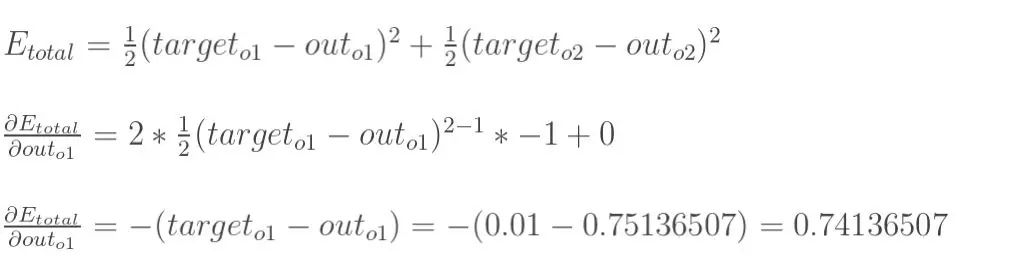Deep Learning 基础

原创： 施天璐  Refinitiv创新实验室ARGO

本文含有部分易懂的数学公式，预计阅读时间10分钟

本文是深度学习的基础入门篇，着重描述以下三个部分：

• 什么是深度学习

• 人工神经网络的概念

• 反向传播算法的理解

 

一 什么是深度学习

深度学习正处于计算机领域的最前沿，也是数据科学和计算机科学领域最火热的话题之一。最近几年，人们时常提起深度学习，机器学习或者人工智能。几乎每一家互联网公司都在AI 探索中投入了大量的人力物力和财力。当这些术语不时在我们耳旁响起的时候，人们也许会好奇，这些术语之间到底是一种怎样的关系。

表达他们之间关系的最好的方式大概是将它们用同心圆来可视化地表现出来。

 

（图片来源：  https://blog.algorithmia.com/introduction-to-deep-learning/）

 

深度学习是机器学习的一个特定子集，机器学习又是人工智能的一个子集。对于每个单独的定义来说：

• 人工智能是宽泛意义上让机器可以像人类一样智能思考

• 机器学习是实现上述目的的方式，它利用算法去搜集出数据背后隐藏的规律

• 深度学习则是利用人工神经网络来实现机器学习的一种方式

既然深度学习的基础是人工神经网络，那我们接下来有必要了解一下人工神经网络。

 

二 人工神经网络的概念

人工神经网络，故名思议，是从生物神经网络受到启发，从而用计算机的方式实现神经网络的一种技术。而实际上，有如人类从鸟类受到启发而发明了飞机，但飞机的速度和续航远超鸟类一样，人工神经网络虽然仿生，但其设计也并不完全受限于生物的表现形式，从而能展现出超越人类的能力。本节先从生物学角度观察神经元，并由此介绍感知机模型。

i) 生物神经元、人工神经元以及神经网络

 

 

（图片来源：  http://shakthydoss.com/technical/deep-learning-for-layman/）

生物学意义上的神经元由接受电信号的树突，负责处理电信号的细胞体，向其他神经元发出信号的轴突组成。每个神经可能有多个树突，但只有一个轴突。如上图右边所示，抽象成函数模型f(x)，其不少于一个输入信号，但是只有一路输出信号。但是注意，虽然轴突只有一路输出，但是并不意味着轴突下游只能接一个树突，轴突可能会有多个突触对接不同的树突。

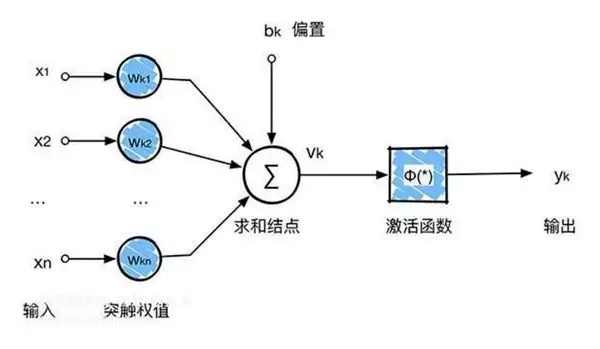
人工神经元是对生物学意义上的神经元的模拟，由几路输入（如树突），一个处理函数（如细胞体）和一路输出（如轴突）组成。用方程的形式表示，输入可以表示为：

人工神经网络则是由很多个上述的神经元组成。其典型连接如下图所示

 

（图片来源：  http://ufldl.stanford.edu/tutorial/）

 

ii) 感知机(Perceptron)

在有了神经元，人工神经网络的基本概念之后，接下来的一部分将会介绍在人工神经网络历史上有着浓重一笔的感知机。1957 年，Frank Rosenblatt 提出了感知机。感知机是神经网络和SVM算法的基础。它是一个线性二分类模型。

（图片来源：  https://blog.csdn.net/White_Idiot/article/details/68952338）

在感知机模型中，激励函数是一个阶跃函数。因此，感知机的预测函数为：

感知机的学习过程

假设数据集线性可分，那么训练感知机的目的就是找到可以正确划分训练集的超平面，即是找到合适的w 和b 参数，使得损失函数最小。但是感知机的损失函数怎么选择呢？

我们知道，已分类点到超平面的距离公式是：

 

其中，

是L2范数。 

 

感知机的样本标签一般设定为1，-1。所以，对于误分类样本：

当时，有。

所以，误分类样本的距离公式为

 

取所有误分类样本集M的所有距离之后，我们得到了其损失函数：

同样，要训练这个模型，又回到了函数求解极值问题。这里一般使用的是梯度下降方法，不再详细展开。

感知机的局限

尽管感知机在机器学习领域掀起了不小的浪潮，它的缺点也迅速为人所知。单层的感知机并不能解决非线性分类的问题（例如模拟一个简单的异或XOR函数）。Marvin Minsky 曾经发表了一本叫做《感知机》的书来指出感知机的不足。

对于非线性问题来说，只能依靠多个计算层来解决。

但是，因为没有办法得知一个权重的小小的变化会怎样影响其余神经元的输出，所以除了随机变换各连接之间的权重之外，并没有简单有效的方法来进行训练多层网络。这个缺陷导致人工神经网络的研究进入了多年的停滞期，直至反向传播算法（BP算法）的提出。

 

三 反向传播算法(Backpropagation)

1986 年，Rumelhar 和Hinton 提出了反向传播(BP)算法来解决多层神经网络计算的复杂性的问题，将神经网络又重新带回到人们的视野中。在这里不详述BP算法的倒推公式，我们将以一个例子向读者们展示BP算法的计算过程。

示例前，有必要知道的是，在多层的神经网络中，激活函数一般用Sigmoid函数代替感知机中的阶跃函数。也就是说，逻辑回归模型成为神经网络的一个基本单元。

示例

为了防止有过多复杂的数学公式，这里仅仅展示一个双层网络的简单模型，并且仅用一条训练数据做参数估计来展示BP算法的原理。（例子来源参考 :  https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/）

假设一个神经网络如下图所示：

 

 

第一层是含有两个神经元的输入层i1、i2以及偏置b1，第二层为隐藏层，包含两个神经元h1、h2 和偏置b2, 第三层为输出层o1和o2。每条线上的w1...w8 代表神经元和各层之间的权重。

现在我们先给它们一个初始值。

我们的目标是当给定输入i1 和i2(0.05 和0.10) 时，使它们的输出接近原始输出o1和o2(0.01 和0.99)。

Step 1：正向传播过程

输入层 到 隐藏层

计算神经元h1 的总输入：

h1的输出：

以同样的方法计算h2 的输出：

隐藏层到输出层

计算神经元o1,o2 的输入和输出：

同样方法计算得到，

到这里前向传播的过程就结束了，我们得到结果[0.75136079, 0.772928465]，与实际值[0.01,0.99]相差甚远。所以现在我们使用反向传播法来更新这些权值。

Step 2：反向传播过程

计算损失

通过采用平方误差公式计算损失：

因为我们有两个输出，所以我们分别计算误差然后求和。

更新隐藏层与输出层之间的权重

以w5 为例。如果我们想知道w5 对于最后的总误差有多大影响，即偏导。根据链式求导法则有：

用图来描述这个过程如下：

 

我们可以分别计算分解出来的三个部分

 ：

：

根据sigmoid 函数的特性，这部分的偏导是o1 输出乘以(1-o1 输出)

：

 

于是，三者相乘得：

 

现在我们得到了 对的偏导。可以根据该偏导值以及梯度下降法更新的设定值：

以同样的方式更新：

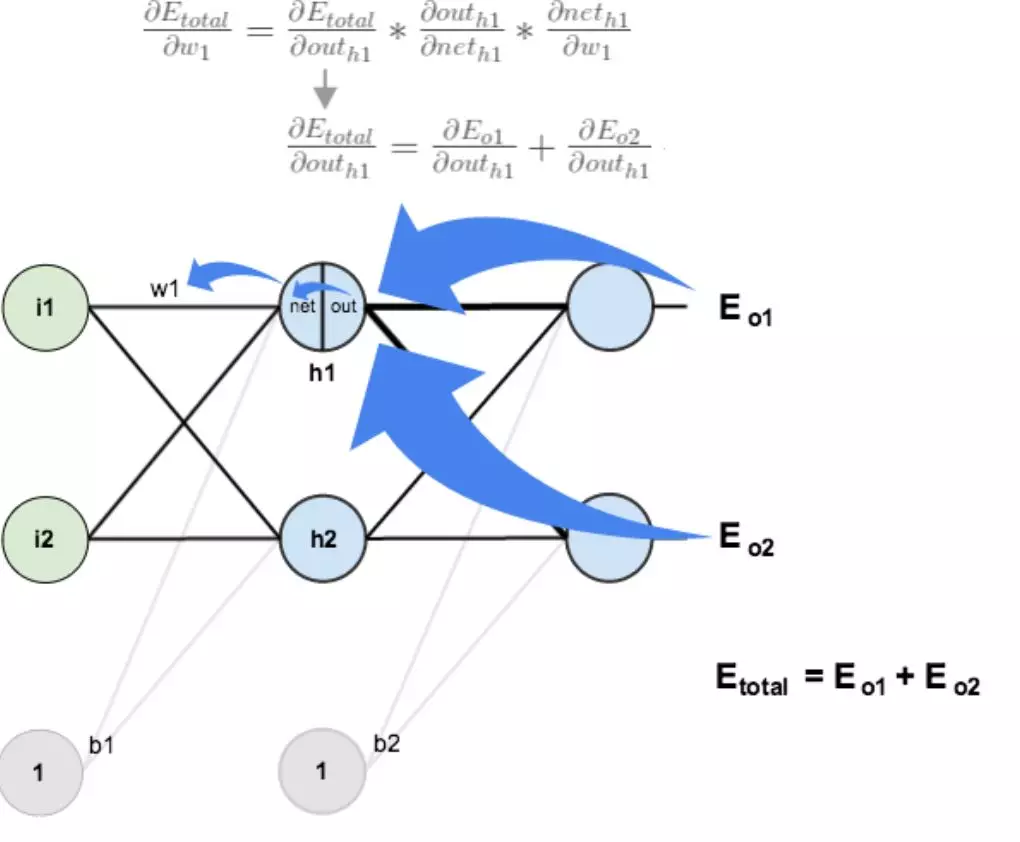
更新隐藏层之间的权重

方法其实与上面类似，见下图

 

（图片来源: https://en.wikipedia.org/wiki/Chain_rule）

 

在隐含层之间的权值更新时，会影响 和，因此  需要考虑两个输出神经元。

 

得：

类似的，

这一轮更新完权重参数w1~w4，一轮误差反向传播法就完成了，在本例的第一次迭代之后，对于输入0.05 和0.1，总误差 由0.298371109 下降至0.291027924。一轮迭代的变化看上去也许很小，但是当如此迭代10000 次后，总误差降到0.000035085，输出为[0.015912196,0.984065734](对比[0.01,0.99])就比较明显了，这也是梯度下降的精髓所在。

 

总结

上述例子是对于反向传播算法的一个小小的演示。反向传播算法的优点在于它能够快速计算出所有偏导，训练神经网络的速度得到了极大的加快。正是因为反向传播算法，神经网络才能得到复兴并被大量应用。反向传播也是深度学习不可或缺的一部分，不过反向传播算法也不是万能的。80 年代后期，人们触及到了性能的瓶颈，利用反向传播算法来训练深度神经网络时尤为明显，由于篇幅的限制，会在以后的文章里介绍现代计算机和新的想法是如何训练深度神经网络的。

好了，深度学习基础介绍就到着这里了。我们的公众号从这期开始，将交叉为大家讲解深度学习基础部分和基本机器学习领域的一些算法，愿读者朋友们关注我们的公众号，与我们一同进步。