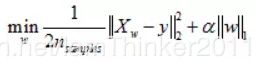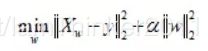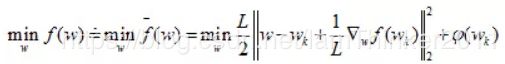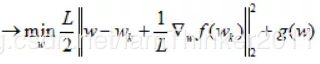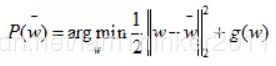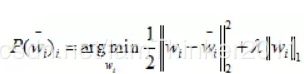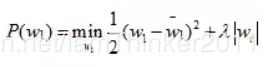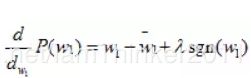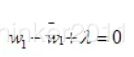专家观点:L1正则稀疏?
原创:轮回Pan Refinitiv创新实验室ARGO
机器学习中为了防止模型过拟合,通常会引入正则化(也称之为惩罚项)。常见的正则化有L1正则和L2正则,两者各有优缺点,而这里我们的关注点是为什么L1正则能导致模型参数稀疏化,而L2不能?
以线性回归为例,其损失函数Loss加上正则项后的形式
I . 形象解释
首先咱们来看看网上流传的一种形象化的解释,大家一定见过下面这两幅图:
图1 L1正则化Loss Function
图2 L2正则化Loss Function
假设有如下带L1正则化的损失函数:
其中J0是原始的损失函数,后面的一项是L1正则化项,α是正则化系数。因为L1正则化是权值的绝对值之和,J0是带有绝对值符号的函数,因此J是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当在原始损失函数J后添加L1正则化项时,相当于对J0做了一个约束。令L=α∑|w|,则J=J0+L,此时变成在L约束下求出J0取最小值的解。考虑二维的情况,即只有两个权值w1和w2,此时L=|w1|+|w2|,对于梯度下降法,求解J0的过程可以画出等值线,同时L1正则化的函数L也可以在w1w2的二维平面上画出来。如图1所示。图中等值线是J0的等值线,黑色方形是L函数的图形。在图中,当J0等值线与L图形首次相交的地方就是最优解。上图中J0与L在L的一个顶点处相交,这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)。可以直观想象,因为L函数有很多『突出的角』(二维情况下四个,多维情况下更多),J0与这些角接触的机率会远大于与L其它部位接触的机率,而在这些角上,会有很多权值等于0,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的黑色方框) ;α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。
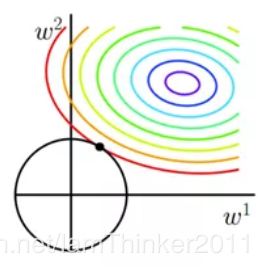
同样可以画出带L2正则化的损失函数如图2所示。二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此J0与L相交时使得w1或w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
也许你已经发现,L1范数下可以导致稀疏,并不是L1范数下一定导致稀疏,还得看原问题的最优解到底在哪个地方取值。
II .数学推导
当然以上只是形象的理解,现在咱们试图从其数学推导上对L1,L2进行分析。我们的目的是最小化损失函数:
从![]() 到
到![]() ,有
,有![]() ,
,
在![]() 的邻域
的邻域![]() 内,有
内,有
根据proximal operator,
i) 当![]() 时, 有
时, 有![]()
因为w在各个维度上互不影响,所以求整体最小可转化成求每个维度上最小,即
那么,  ? 答案是 0,至此,我们就推出了L1正则会导致稀疏。
? 答案是 0,至此,我们就推出了L1正则会导致稀疏。
补充说明:
同样的方法可以用到L2正则,因为L2正则损失函数可导,所以可推出w取不到0,因此L2正则无法实现权重稀疏和特征选择。
III . 代码实现部分
我们看到在tensorflow代码关于LASSO实现部分中它注释到当A小于0.9时,heavyside_step变为0,直接实现稀疏性,简单粗暴,而L2则没有。
if regression_type == 'LASSO':
# Declare Lasso loss function
# Lasso Loss = L2_Loss + heavyside_step,
# Whereheavyside_step ~ 0 if A < constant, otherwise ~ 99
lasso_param = tf.constant(0.9)
heavyside_step = tf.truediv(1., tf.add(1., tf.exp(tf.multiply(-50.,tf.subtract(A, lasso_param)))))
regularization_param = tf.multiply(heavyside_step, 99.)
loss = tf.add(tf.reduce_mean(tf.square(y_target - model_output)),regularization_param)
elif regression_type == 'Ridge':
# Declare the Ridge loss function
# Ridge loss = L2_loss + L2 norm of slope
ridge_param = tf.constant(1.)
ridge_loss = tf.reduce_mean(tf.square(A))
loss = tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target -model_output)), tf.multiply(ridge_param, ridge_loss)), 0)
参考资料:
CSDN的 https://blog.csdn.net/jinping_shi/article/details/52433975