关于Prim算法的个人理解

既然接触了最短路径算法，也就肯定会接触最小生成树中的Prim算法。

Prime算法主要是来从一个无向图（注意，是无向图）来生成一个权值和最小的最小生成树（一定无环），最小生成树当然权值和唯一但是生成树的结构不唯一。Prim算法的主体构造和迪杰斯特拉算法极其相似，并且采用的都是贪心思想，也就是在选取当前最小的权值边，加入该边对应的节点，从而进行构造；

其主要的思路和流程如下所示：

对于主体来说，我们维护一个集合，集合里包含点，点就是已经确定作为生成树节点。每次操作将不在集合内的点加入集合中，从而最后使得构成一个树。

在进行点选取加入集合之前，先将集合内的所有点的到达未纳入集合点的边进行权值比较，找出权值最小的那个边，将指向的点纳入集合，将边视为树中的指向。重复进行，直至一个树生成。

理解起来还是很容易的，对于代码部分，则要进行抽象，和迪杰斯特拉算法相同，还是维护一个distance数组，该数组代表的意义是集合到达其他点的距离，可以看成到欲归纳点的边的权值大小，而不再是迪杰斯特拉中起点到其他点的距离。

所以，代码方面还是大同小异：

仍然是构建图、d数组，是否访问过的标志数组；

主体方面仍然需要注意一下:

如下所示：

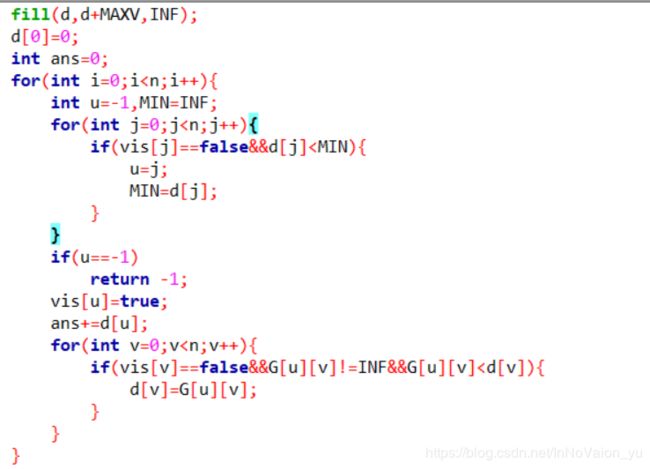
其中ans代表整个图的权值和，仍然对d[0]赋值，来保证第一步将0节点纳入集合。

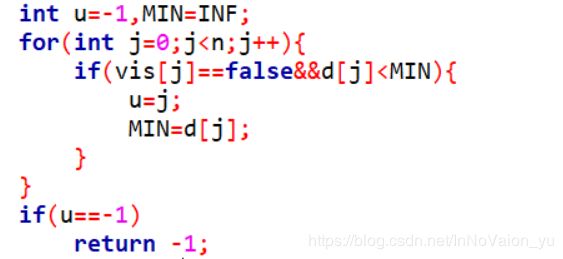
该循环和迪杰斯特拉的目的略有不同，目的是寻找欲归纳点中距集合最小的点，距离近也就说明边的权值小，从而获得其节点，要把她归纳到集合中作为树节点；

下一个循环则是进行distance更新，来为下一个点归纳做准备。由于新归纳进一个点进集合，该点到达欲归纳点的权值可能小于先前集合中的其他点，所以进行权值的代替和更新；

总体代码如下所示：

const int MAXV=1000;
const int INF=1000000000;
int n,G[MAXV][MAXV];
int d[MAXV];
bool vis[MAXV];
int prim(){
    fill(d,d+MAXV,INF);
    d[0]=0;
    int ans=0;
    for(int i=0;i