BP 神经网络算法识别MNIST数据集

BP 神经网络算法识别MNIST手写数字数据集

人工神经网络的基本原理

生物神经元在结构上由:

1. 细胞体(Cell body)
2. 树突(Dendrite)
3. 轴突(Axon)
4. 突触(Synapse)

四部分组成。用来完成神经元间信息的接收、传递和处理。

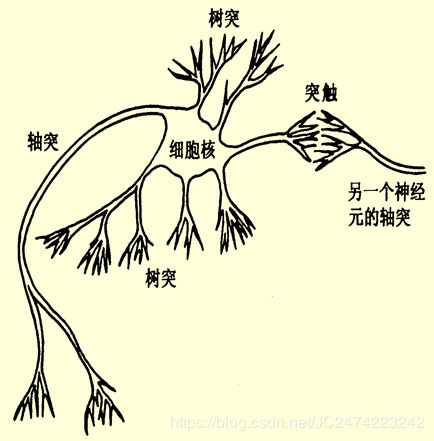
神经元及其突触是神经网络的基本器件。因此，模拟生物神经网络应首先模拟生物神经元, 人工神经元(节点)从三个方面进行模拟:

1. 节点本身的信息处理能力
2. 节点与节点之间连接(拓扑结构)
3. 相互连接的强度(通过学习来调整)

神经元模型

一般地，将形式神经元模型表示为下图所示的一个具有多输入-单输出的非线性阈值器件。

$x_1,x_2,\dots ,x_n$表示某一神经元的第n个输入; $W_{ij}$表示第$i$个神经元与第$j$个神经元的突触连接强度，其称为权值。神经元模型将这些输入加权后经激励函数$f$输出。
$$A_j=\sum _{j=1}^n{x}_i{W}_{ij}-{\Theta }_j$$
$$O_j=f(A_j)$$

几个常见的神经元模型

1. 阈值型
   该类型的神经元具有一个设定的阈值，是一种最简单的神经元，当加权后的输入大于阈值时，输出为1，否则为0。
   激励函数一般表示为：
   $$y_i=f(A_i)=\{\begin{array}{l}1,A_i>{\Theta }_i\\ \\ 0,A_i\le {\Theta }_i\end{array}$$
   对于阈值型神经元, 其输入权值$W_{ij}$可在$(-1,+1)$区间连续取值。负值表示抑制，正值表示加强。
2. 线性饱和型
   线性饱和型神经元在一定区间内，输入输出满足线性关系。激励函数为：
   $$y_i=f(A_i)=\{\begin{array}{l}0,A_i<0\\ \\ C{A}_i,0\le A_i\le A_c\\ \\ 1,A_i>A_c\end{array}$$
   $C$为常量
3. S(sigmoid)型
   S型神经元是一类连续型神经元模型，采用S型函数(sigmoid 函数)。其激励函数为：
   $$y_i=f(A_i)=1/(1+e^{A_i})$$
   或
   $$y_i=f(A_i)=1/(2(1+th(A_i/A_0)))$$
4. 子阈累积型
   这类神经元的激活函数也是一个非线性的。当所产生的激活值超过$T$值时，该神经元将被激活。在线性范围内，系统反响是线性的。子阈的一个作用是抑制噪声，即对小的随机输入不产生响应。
5. 概率型
   其输出状态的0或1将根据激活函数的大小按照一定的概率来确定。
   假定神经元为1的概率为：
   $$P(S_i=1)=1/(1+e^{\frac{A_i}{T}})$$
   则，状态为0的概率为:
   $$P(S_i=0)=1-P(S_i=1)$$
   玻尔兹曼神经元就是这一类神经元。

多层前向神经网络及BP学习算法

单层前向神经网络的缺点是只能解决线性可分的分类问题，要增强网络的分类能力唯一的方法是采用多层网络。也就是在输入层和输出层之间加入隐层，这就构成了多层感知机。

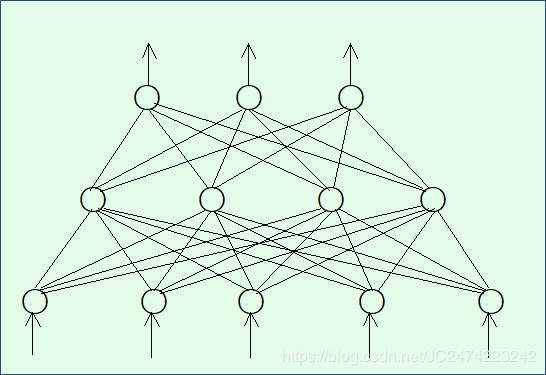
BP学习算法

在BP学习算法中：

1. 工作信号正向传播;
2. 误差信号反向传播。

BP算法的具体步骤如下(三层的BP学习算法)：

1. 设置变量和参量:
   1. 输入数据将被作为一个$n$维的输入向量$x_k=[x_{k1},x_{k2},\dots ,x_{kN}](k=1,2,\dots ,N)$或称训练样本; $N$为训练样本的个数。设：
      $$W_{IH}(n)=\left[\begin{array}{cccc}{w}_{11}(n)& w_{12}(n)& \dots & w_{1H}(n)\\ & & & \\ w_{21}(n)& w_{22}(n)& \dots & w_{2H}(n)\\ & & & \\ ⋮& ⋮& \ddots & ⋮\\ & & & \\ w_{I1}(n)& w_{I2}(n)& \dots & w_{IH}(n)\end{array}\right]$$
      为第$n$次迭代时,输入层和隐层之间的权值矩阵。
      $$W_{HO}(n)=\left[\begin{array}{cccc}{w}_{11}(n)& w_{12}(n)& \dots & w_{1O}(n)\\ & & & \\ w_{21}(n)& w_{22}(n)& \dots & w_{2O}(n)\\ & & & \\ ⋮& ⋮& \ddots & ⋮\\ & & & \\ w_{H1}(n)& w_{H2}(n)& \dots & w_{HO}(n)\end{array}\right]$$
      为第$n$次迭代时,隐层和输出层之间的权值矩阵。
   2. $Y_k(n)=[y_{k1}(n),y_{k2}(n),\dots ,y_{kN}(n)](k=1,2,\dots ,N)$为第$n$次迭代时网络的实际输出
   3. $d_k(n)=[d_{k1}(n),d_{k2}(n),\dots ,d_{kN}(n)](k=1,2,\dots ,N)$为第$n$次迭代时网络的期望输出。由于在本次实验中使用的是S型神经元,其特性不能达到渐进值$+\alpha$ 和 $-\alpha$, 故期望输出应当取接近渐进值的值，而不是取$+\alpha$ 和 $-\alpha$。
   4. $\eta$ 为学习效率, $n$为迭代次数。
2. 初始化，赋给$W_{IH}(0),W_{HO}(0)$各一个较小的随机非零值，建议初始值分布在区间$(-2.4/F,2.4/F)$或$(-3/\sqrt{F},3/\sqrt{F})$之间。$F$为所连单元的输入端个数。
3. 输入随机样本$x_k$,并置$n=0$
4. 对输入样本$x_k$,前向计算BP神经网络每层的输入信号 $u$ 和输出信号 $v$。其中
   $$v_o^O(n)=y_{ko}(n)o=1,2,\dots ,O$$
5. 由期望输出$d_k$和上一步求得的实际输出$Y_k(n)$计算误差$E(n)$判断其是否满足要求，如满足要求转至第8步。
6. 判断$n+1$是否大于最大迭代次数，若大于转至第8步，否则对输入样本$x_k$反向计算每层神经元的局部梯度$\delta$。其中:
   $${\delta }_o^O(n)=y_o(n)(1-y_o(n))(d_o(n)-y_o(n))o=1,2,\dots ,O$$
   $${\delta }_h^H(n)=f^{\prime }(u_h^H(n))\sum _{h=1}^H{\delta }_o^O(n)w_{ho}(n)h=1,2,\dots ,H$$
7. 按下式计算权值修正值$\Delta w$,并修正权值; $n=n+1$, 转至第4步:
   $$\Delta w_{ho}(n)=\eta {\delta }_o^O(n)v_h^H{w}_{ho}(n+1)=w_{ho}(n)+\Delta w_{ho}(n)$$
   $$\Delta w_{ih}(n)=\eta {\delta }_h^H(n)v_i^I{w}_{ih}(n+1)=w_{ih}(n)+\Delta w_{ih}(n)$$
8. 判断是否学完所有的训练样本，若是则结束，否则转回第3步。

注:

对于一个训练周期训练多个样本的的训练模式，修正值的计算函数方法如下:
$$E_{av}=\frac{1}{N}\sum _{k=1}^N{E}_k=\frac{1}{2N}\sum _{k=1}^N\sum _{p=1}^P{e}_{kp}^2$$
其中，$e_{kp}^2$为网络输入第$k$个训练样本时输出神经元$p$的误差。

学习步长$\eta$值的选取比较重要，$\eta$值过大会引起网络震荡，过小则会导致收敛速度太慢

隐层个数的选取有两种：

1. 大于${\log }_{2}F$,$F$为该层的输入节点个数
2. $\sqrt{I+O}+a$ 其中,$a$为一个$1-10$的修正值，$I,O$分别为输入层和输出层的节点个数

BP学习算法并不完善，它主要存在一下缺陷：学习收敛速度太慢，网络的学习记忆具有不稳定性。

python实现

class BPNet:
    def train(self):
        labels = []
        with open(train_labels_idx1_ubyte_file, "rb") as file:
            magicNumber, labelsSize = struct.unpack('>ii', file.read(8))
            if magicNumber == 2049:
                print("label")
            else :
                print("Can't recognized")
                return 0
            labels = file.read()
        with open(train_images_idx3_ubyte_file, "rb") as file:
            magicNumber, numOfImages, rowsNum, columnsNum = struct.unpack('>iiii', file.read(16))
            if magicNumber == 2051:
                print("image")
            else :
                print("Can't recognized")
                return 0
            # 神经元节点
            # 输入层, 隐层, 输出层
            inputLayerNodeNum, hideLayerNodeNum, outputLayerNodeNum = rowsNum * columnsNum, 120, 10
            # 权值
            self.weightIH, self.weightHO = [[] for i in range(inputLayerNodeNum)], [[] for i in range(hideLayerNodeNum)]
            self.weightGenerator(self.weightIH, inputLayerNodeNum, hideLayerNodeNum)
            self.weightIH = np.array(self.weightIH)
            self.weightGenerator(self.weightHO, hideLayerNodeNum, outputLayerNodeNum)
            self.weightHO = np.array(self.weightHO)
            count, formatStr, yita = 0, '>' + str(inputLayerNodeNum) + 'B', 0.1
            while count < numOfImages:
                pixes = np.array([struct.unpack(formatStr, file.read(inputLayerNodeNum))])
                Ioutput = 1 / (1 + np.exp(-1 * pixes))
                Houtput = self.f(Ioutput, self.weightIH)
                Ooutput = self.f(Houtput, self.weightHO)
                EO = Ooutput * (1 - Ooutput) * (self.d(labels[count]) - Ooutput)
                EH = Houtput * (1 - Houtput) * (self.weightHO @ EO.T).T
                self.weightHO = self.weightHO + yita * Houtput.T @ EO
                self.weightIH = self.weightIH + yita * Ioutput.T @ EH
                count = count + 1
                if np.mod(count, 1000) == 0:
                    print("已训练 " + str(count) + " 张图片")
            self.test()