Floyd算法（任意两点间的最短路径）

Floyd（弗洛伊德）算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd算法的时间复杂度为O(N³)，空间复杂度为O(N²)。

算法思想：

     Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

      从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

算法步骤：

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

给出矩阵，其中矩阵A是邻接矩阵，而矩阵Path记录u,v两点之间最短路径所必须经过的点

用处：可以通过以每个顶点作为源点循环求出每对顶点之间的最短路径，也可以用于求两顶点之间最短路径。

通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵。

其状态转移方程如下： D(k)[i,j]:=min{D(k-1)[i,k]+D(k-1) [k,j], D(k-1)[i,j]}；

优化后map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}

map[i,j]表示i到j的最短距离是穷举i,j的断点，map[n,n]初值应该为0，或者按照题目意思来做。

#include 
#define MAXV 100
#define INF 9999
typedef struct{
int edges[MAXV][MAXV];
int n,e;
}MGraph;
void ppath(int path[][MAXV],int i,int j)
{
	int k;
	k=path[i][j];
	if (k==-1)  return;
	ppath(path,i,k);
	printf("%d,",k);
	ppath(path,k,j);
}
void DisPath(int A[][MAXV],int path[][MAXV],int n)
{
	int i,j;
	for (i=0;i(A[i][k]+A[k][j]))
				{	A[i][j]=A[i][k]+A[k][j];
					path[i][j]=k;
				}
	}
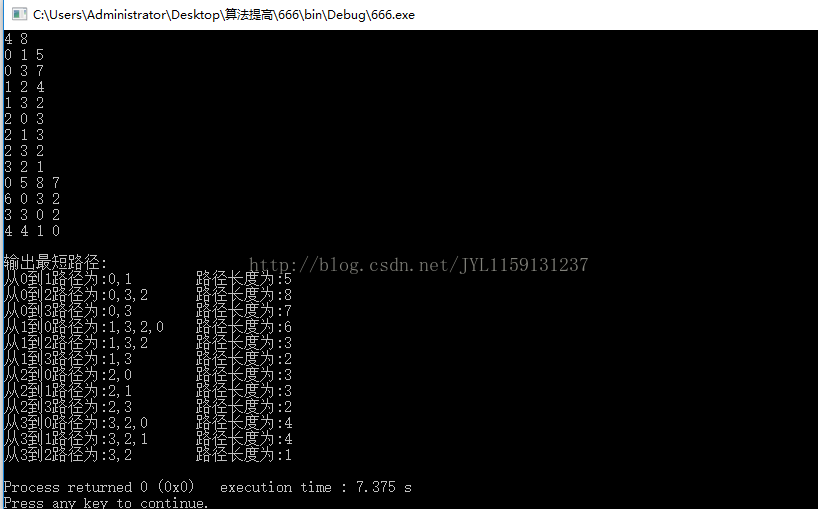
	printf("\n输出最短路径:\n");
	DisPath(A,path,n);			//输出最短路径
}
void DispMat(MGraph g)
//输出邻接矩阵g
{
	int i,j;
	for (i=0;i

还是以上次的图为例

参考博客：最短路径—Dijkstra算法和Floyd算法 

对于两种算法的思想讲的比较详细，不懂得可以看一下。

https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html

#include 
#define MAXV 100
#define INF 99999
int A[MAXV][MAXV],path[MAXV][MAXV];
typedef struct
{
    int edges[MAXV][MAXV];
    int n,e;
} Mg;
void ppath(int i,int j)
{
    int k;
    k=path[i][j];
    if (k==-1)
        return;
    ppath(i,k);
    printf("%d,",k);
    ppath(k,j);
}
void DisPath(int n)
{
    int i,j;
    for (i=0; i(A[i][k]+A[k][j]))//注意判断条件
                {
                    A[i][j]=A[i][k]+A[k][j];
                    path[i][j]=k;
                }
    }
    for(i=0;i0; i--)
    {
        int v1,v2,Q;
        scanf("%d %d %d",&v1,&v2,&Q);
        g.edges[v1][v2]=Q;
    }
    floyd(g);
    return 0;
}