Java数据结构和算法-栈和队列(4-解析算术表达式)
解析算术表达式,例如3+4*5等和之前所学的例子匹配分隔符类似,都是利用栈来实现的,只不过解析算术表达式会更复杂一些。
计算机算法直接求算术表达式是很难的,但是通过下面两个步骤实现算法会相对容易很多:
- 将算术表达式转换为另一种表达式:后缀表达式。
- 计算后缀表达式的值。
在研究两个步骤的具体实现之前,我们先介绍后缀表达式。
后缀表达法
在生活中,我们使用的都是中缀表达式,即将操作符放在两个操作数的中间,比如:3+5,4/6等。
在后缀表达式中(又称波兰逆序表达式,或RPN),操作符放在了两个操作数的后面,这样中缀表达式就可以变为后缀表达式,例如:A+B变为AB+。其他例子如下表:
| 中缀表达式 | 后缀表达式 |
|---|---|
| A+B-C | AB+C- |
| A*B/C | AB*C/ |
| A+B*C | ABC*+ |
| A*B+C | AB*C+ |
| A*(B+C) | ABC+* |
| A*B+B*C | AB*BC*+ |
| (A+B)*(D-C) | AB+DC-* |
| ((A+B)*C)-D | AB+C*D- |
| A+B*(C-D/(E+F)) | ABCDEF+/-*+ |
其实算术表达式中可能还会有^这个操作符,并且可能还存在多位数字运算的操作符,但为了简单介绍栈在解析算术表达式中的应用,在这里我们暂且不讨论。
中缀表达式与后缀表达式之间的转换
为了明白中缀表达式是怎么转换为后缀表达式的,并且后缀表达式是怎么计算的,计算一个算术表达式,对应计算机而言是困难的,但对于人们来说却再简单不过了,或许通过分析人们对于算术表达式的计算,我们可以得到一些启示。所以我们先从怎么计算中缀表达式值入手。
粗略地将,“算”表达式的值要遵循下面几个原则:
- 从左到右依次读取表达式的
- 已经读到了两个操作数和一个操作符时就可以计算,并用计算结果代替这两个操作数和一个操作符。不过在碰到更高优先级的操作符,不能计算,而应该暂且保存这几个操作数和操作符。
- 从左到右一直都下去,能算就算,一直到结束为止。
下面的三个表显示了三个十分简单的中缀表达式的求值的例子:
例1:3+4-5
| 读取元素 | 解析后的表达式 | 备注 |
|---|---|---|
| 3 | 3 | |
| + | 3+ | |
| 4 | 3+4 | |
| - | 7 | 遇到-时,先计算3+4的值 |
| 7- | ||
| 5 | 7-5 | |
| end | 2 | 表达式读完,计算剩余的值 |
在这个例子中,只有看到4之后的操作符才能判断是否要计算3+4的值,如果遇到的是*或/,由于优先级。那么就不能先计算,比如下面的例2,但是此处遇到的是-,与+同级,所以先计算3+4的值。
例2:3+4*5
| 读取元素 | 解析后的表达式 | 备注 |
|---|---|---|
| 3 | 3 | |
| + | 3+ | |
| 4 | 3+4 | |
| * | 3+4* | 遇到*时,优先级大于+ |
| 5 | 3+4*5 | |
| 3+20 | ||
| end | 23 | 表达式读完,计算剩余的值 |
例3:3*(4+5)
| 读取元素 | 解析后的表达式 | 备注 |
|---|---|---|
| 3 | 3 | |
| * | 3* | |
| ( | 3*( | |
| 4 | 3*(4 | 遇到了(,所以不能先计算3*4 |
| + | 3*(4+ | |
| 5 | 3*(4+5 | |
| ) | 3*(4+5) | |
| 3*9 | 遇到),计算括号内的值 | |
| end | 27 |
在上述的例子中,由于(的出现,覆盖了之前优先级,需要先计算出()内的结果才能计算外部。
正如上面的三个例子所示,中缀表达式计算其值时,必须向前(从左到右)读取两个操作数和一个操作符。等到有足够的条件进行运算时,又要向后读取这两个操作数和一个操作符,从而来进行运算。有时如果在向前读时遇到了更高的操作符,那么就必须推迟运算,先进行后面级别高的运算,然后再回过头(向左)来执行前面的运算。
我们可以直接利用上述过程实现算法,但是利用后缀表达式可以更加简单一些。
中缀表达式转换为后缀表达式
中缀表达式转为后缀表达式和之前求中缀表达式的值类似,不同之处在于,中缀表达式转为后缀表达式不用做算术运算,不求中缀表达式中的值,而只是将中缀表达式的操作数和操作符重新排列成另一种形式:后缀表达法。然后再计算后缀表达式的值。
和求中缀表达式的值得过程一样,先从左向右依次读取字符。当读取到操作数时就毫不犹豫地将它复制到后缀字符串中,如果是操作符则等到要利用该操作符求某两个操作数的值时,再将其复制到后缀字符串中去。
具体过程如下三个例子:
- 例1:A+B-C
| 读取的字符 | 分解中缀表达式的过程 | 求后缀表达式的过程 | 注释 |
|---|---|---|---|
| A | A | A | |
| + | A+ | A | |
| B | A+B | AB | |
| - | A+B- | AB+ | 读到-与+同级,+被利用 |
| C | A+B-C | AB+C | |
| end | A+B-C | AB+C- | 结束时,-被利用 |
- 例2:A+B*C
| 读取的字符 | 分解中缀表达式的过程 | 求后缀表达式的过程 | 注释 |
|---|---|---|---|
| A | A | A | |
| + | A+ | A | |
| B | A+B | AB | |
| * | A+B* | AB | 读到*比+高优先级 |
| C | A+B*C | ABC | |
| A+B*C | ABC* | *被利用求BC的乘积,所以复制 | |
| end | A+B*C | ABC*+ | 结束时,+被利用 |
- 例3:A*(B+C)
| 读取的字符 | 分解中缀表达式的过程 | 求后缀表达式的过程 | 注释 |
|---|---|---|---|
| A | A | A | |
| * | A* | A | |
| ( | A*( | A | |
| B | A*(B | AB | 读到(,覆盖*的优先级 |
| + | A*(B+ | AB | |
| C | A*(B+C | ABC | |
| ) | A*(B+C ) | ABC | |
| A*(B+C ) | ABC+ | 遇到),括号内的+被利用 | |
| end | A*(B+C ) | ABC+* | 结束时,*被利用 |
如上述三个例子,在数字求值过程中,需要向前和向后读取中缀表达式,已完成转换,当某个操作符后面遇到更高优先级的操作符或者左括号时,就不能把操作符先复制到后缀表达式当中。那么按照这种原则,后缀表达式中高优先级的操作符就必须比低优先级的操作符先写到后缀表达式当中。
栈中的操作符
中缀转为后缀的过程中,操作符的顺序是相反的。因为在第一个操作符必须在第二个操作符输出之前输出。所以后缀操作符的顺序和中缀操作符中的顺序是相反的。具体例子如下:
- 例1:A+B*(C-D)
| 读取的字符 | 分解中缀表达式的过程 | 求后缀表达式的过程 | 栈中的内容 |
|---|---|---|---|
| A | A | A | |
| + | A+ | A | + |
| B | A+B | AB | + |
| * | A+B* | AB | +* |
| ( | A+B*( | AB | +* ( |
| C | A+B*( C | ABC | +*( |
| - | A+B*( C+ | ABC | +*(- |
| D | A+B*( C+D | ABC | +*(- |
| ) | A+B*( C+D) | ABC- | +*( |
| A+B*( C+D) | ABC- | +* | |
| A+B*( C+D) | ABC-* | + | |
| A+B*( C+D) | ABC-*+ |
从中可以看出中缀表达式中操作符的顺序是+-,但在后缀表达式中其顺序却是-+,这说明利用栈来存取后缀表达式的操作符是一个很好的方法。
从某个方面来讲,从栈中弹出操作符实际上是向左扫描读取的操作符的过程,我们并没有扫描整个字符串,而是只查验操作符和括号。读入的操作符会被压入栈中,当要使用的时候,就会从栈中弹出一个操作符。
而对于操作数,它在中缀和后缀表达式中的顺序是相同的,因此读取到操作数时并不需要将其压入栈中,而是直接复制到后缀字符串后面即可。
转换规则
下表将中缀表达式转换为后缀表达式的过程更明确的表达出来,在下表中,‘>’和‘>=’符合表示两个操作符之间的优先级,opThis表示刚读取的操作符,opTop表示在栈顶位置的操作符。
| 读取到的操作符 | 动作 |
|---|---|
| 操作数 | 直接复制到后缀表达式中 |
| 左括号( | 压入栈中 |
| 右括号) | 栈非空时,完成下面步骤循环 |
| 弹出一项 | |
| 若项不为),则复制到后缀表达式中 | |
| 若项为(,则结束循环 | |
| opThis | 如果栈为空,压opThis入栈 |
| 如果opTop为(,则直接将opThis压入栈中 | |
| 如果opThis>opTop,则直接将opThis压入栈中 | |
| 否则现将opTop弹出,复制到后缀表达式中,则将opThis压入栈中 | |
| 没有更多项 | 栈非空时,将栈中的操作符依次弹出复制到后缀表达式后面 |
现在回过头利用上面的规则再去做前面中缀转换为后缀的例子,上面的规则在转换过程中是十分有用的。
中缀转为后缀的Java代码
再次提醒此处的实现是假设操作符只有简单的加减乘除和括号的,因为这个例子只是为了展现栈的用途。中缀转后缀使用的辅助工具是栈,而栈在前面的介绍中已经实现过了,所以在此处直接使用,不详细写了:
class MyStack {
//...
}
class InToPost {
private String input; //输入的中缀表达式
private String output; //输出的后缀表达式
private MyStack[] stack; //存放操作符的
private int top; //记录栈顶的下标
public InToPost(String s) {
input = s;
stack = new MyStack[s.length()];
top = -1;
output = "";
}
public String doTrans() {
for(int i = 0; i < input.length; i ++) {
char c = input.charAt(i);
switch(c) {
case '(':
stack.push(c);
break;
case ')':
doPop(c, 0);
break;
case '+':
case '-':
doPop(c, 1);
break;
case '*':
case '/':
doPop(c, 2);
break;
default:
output += c;
break;
}//end switch
while(!stack.isEmpty())//结束时判断栈中是否还有操作符
output += stack.pop();//将它们依次输出
return output;
}//end for
}//end doTrans
public void doPop(char opThis, int prio1) {
while(!stack.isEmpty()) {
char opTop = stack.pop();
int prio2;
if(opTop == '(') {
if(prio1 != 0)
stack.push(opTop);
break;
} else {
if(opTop == '+' || opTop == '-')
prio2 = 1;
else
prio2 = 2;
if(prio1 > prio2) {
stack.push(opTop);
break;
}
output += opTop;
}//end else
}//end while
if(prio1 != 0)
stack.push(opThis);
}//end doPop
}//end InToPost
class TransformApp {
public static void main(String[] args) throws IOException {
String input;
while(true) {
System.out.print("Enter infix: ");
System.out.flush();
input = getString();
if("".equal(input))
break;
InToPost inToPost = new InToPost(input);
String output = inToPost.doTrans();
System.out.println("postfix is " + output);
}
}//end main
public String getString() {
InputStreamReader isr = new InputStreamReader(System.in);
BufferedReader br = new BufferedReader(isr);
String s = br.readLine();
return s;
}
}//end TransformApp 后缀表达式求值
中缀表达式转为后缀表达式理解可能比较复杂,但是理解之后是简单的,并且在之后知道怎么求值之后会发现其实它是那么简单。
人们是怎么进行后缀表达式求值的
下图表达了人们对后缀表达式345+*612+/-的求值的过程:
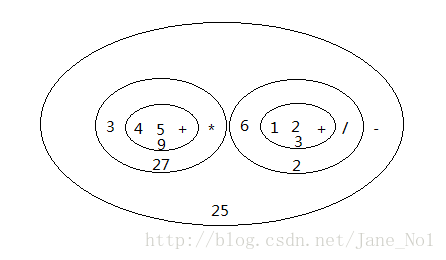
在上述的后缀表达式中,从左到右读取操作符,当遇到第一个操作符时,将它与左边相邻的两个操作数画在同一个圈内,进行运算求值,并将结果写在圈中,如图4+5 = 9。
然后继续向右,遇到第二个操作符*,将它与左边相邻的两个操作数圈在一个一起,因为前一个操作符得到了结果9,所以将这个结果和前一个操作数3与操作符圈在一起,然后求值,3*9=27。将结果写在该圈内。继续该过程,直到所有的操作符都读取完,并得到了相应的值:1+2=3,6/3=2,27-2=25。
后缀表达式的求值原则
根据上述的过程,从左向右,每当遇到一个操作符,就会将在该操作符之前最后看到的两个操作数与该操作符进行运算,而这个特点表明正好可以利用栈来存储操作数。
下面的两点描述了后缀表达式的求值原则:
- 操作数:压入栈中。
- 操作符:从栈中弹出两项进行运算,然后将结果再压入栈中。
后缀表达式的Java代码
和之前一样栈使用之前实现的栈MyStack
class ParsePost {
private String input;
private MyStack stack;
public ParsePost(String s) {
input = s;
stack = new MyStack(s.length());
}
public String doParse() {//对后缀表达式进行求值
int result = 0;
int num1, num2;
char ch;
for(int i = 0; i < input.length(); i ++) {
ch = input.charAt(i);
if(ch >= '0' && ch <= '9')//如果为操作数
stack.push((int)(ch-'0'));//转为int型压入栈中
else {
num1 = stack.pop(); //弹出操作符左边第一个临近的数
num2 = stack.pop(); //弹出操作符左边第二个临近的数
switch(ch) {
case '+':
result = num2 + num1;
break;
case '-':
result = num2 - num1;
break;
case '*':
result = num2 * num1;
break;
case '/':
result = num2 / num1;
break;
default:
result = 0;
break;
}//end switch
stack.push(result);
}//end else
}//end for
result = stack.pop();
return result;
}//end doParse
}//end ParsePost
class PostfixApp {
public static void main(String[] args) throws IOException {
String input;
int output;
while(true) {
System.out.print("Enter postfix");
System.out.flush();
input = getString();
if("".equal(input))
break;
ParsePost parse = new ParsePost(input);
output = parse.doParse();
System.out.println("the result : " + output);
}//end while
}//end main
public static String getString() throws IOException {
InputStreamReader isr = new InputStreamReader(System.in);
BufferedReader br = new BufferedReader(isr);
String s = br.readLine();
return s;
}
}//end PostfixApp 如上述代码所示,在PostfixApp运行时,用户输入后缀表达式,然后调用ParsePost的方法就可以求出后缀表达式对应的值了,当然也可以结合前面的中缀转后缀的过程,这样用户可以直接输入算术表达式,就可以求取其值。
不过前面转换和求值的过程都有一个问题,由于没有检验用户输入的表达式是否格式正确,可能程序会报错或崩溃,这个结果是难以预测的。
通过上面的方法运行程序,可以发现后缀表达式求值要比中缀表达式求值快很多。