BigDecimal中的取整模式

这个类用起来还是很比较复杂的，原因在于舍入模式，数据运算规则太多太多，

不是数学专业出身的人看着中文API都难以理解，这些规则在实际中使用的时候在翻阅都来得及。

在银行、帐户、计费等领域，BigDecimal提供了精确的数值计算。其中8种舍入方式值得掌握。

round_up我把实验结果截图出来，后面的自己去做实验。说实话，真的很难懂。不过一般用四舍五入的取整模式

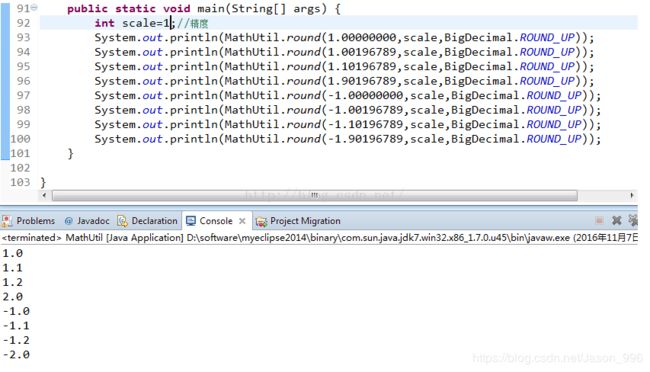
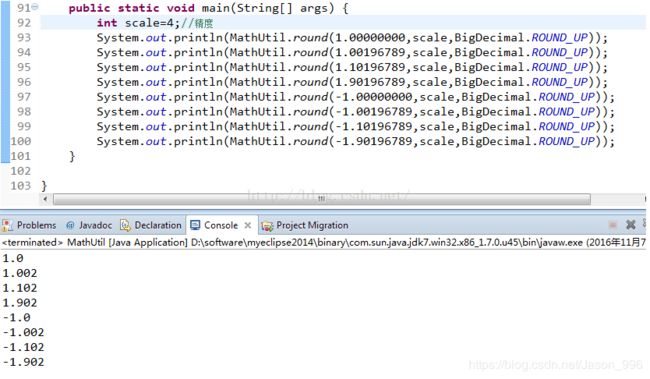
1、ROUND_UP

始终对非舍弃部分前面的数字加1。

0.1203456789,当精度为3的时候，按照round_up模式，结果是0.121

-0.1203456789,当精度为3的时候，按照round_up模式，结果是-0.121

注意：0.1891，当精度为3的时候，按照round_up模式，结果是0.19，自动去掉了9后面的0

而当0.91，当精度为1的时候，按照round_up模式，结果是1.0，保留了唯一一个小数点后面的0

截图好像更加直观一点：大家可以按照我的数据去做试验，（数据都是经过精心筛选的数据）

1）精度1时：

2）精度为2时：

3）精度为3时：

2、ROUND_DOWN

从不对舍弃部分前面的数字加1，即截短。(舍去)

0.1203456789,当精度为3的时候，按照round_down模式，结果是0.12，自动去掉了2后面的0

-0.1203456789,当精度为3的时候，按照round_down模式，结果是-0.12，自动去掉了2后面的0

注意：0.1891，当精度为3的时候，按照round_down模式，结果是0.189，

注意：1.558，当精度为1的时候，按照round_down模式，结果是1.5，

而当0.91，当精度为1的时候，按照round_up模式，结果是1.0，保留了唯一一个小数点后面的0

3、ROUND_CEILING

接近正无穷大的舍入模式。

如果 BigDecimal 为正，则舍入行为与 ROUND_UP 相同;

如果为负，则舍入行为与 ROUND_DOWN 相同。

注意，此舍入模式始终不会减少计算值。

4、ROUND_FLOOR

接近负无穷大的舍入模式。

如果 BigDecimal 为正，则舍入行为与 ROUND_DOWN 相同;

如果为负，则舍入行为与 ROUND_UP 相同。

注意，此舍入模式始终不会增加计算值。

5、ROUND_HALF_UP

向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则为向上舍入的舍入模式。

如果舍弃部分 >= 0.5，则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同。

注意，这是我们大多数人在小学时就学过的舍入模式(四舍五入)。

6、ROUND_HALF_DOWN

向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则为上舍入的舍入模式。

如果舍弃部分 > 0.5，则舍入行为与 ROUND_UP 相同;否则舍入行为与 ROUND_DOWN 相同(五舍六入)。

7、ROUND_HALF_EVEN

向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则向相邻的偶数舍入。

如果舍弃部分左边的数字为奇数，则舍入行为与 ROUND_HALF_UP 相同;

如果为偶数，则舍入行为与 ROUND_HALF_DOWN 相同。

注意，在重复进行一系列计算时，此舍入模式可以将累加错误减到最小。

此舍入模式也称为“银行家舍入法”，主要在美国使用。四舍六入，五分两种情况。

如果前一位为奇数，则入位，否则舍去。

以下例子为保留小数点1位，那么这种舍入方式下的结果。

1.15>1.2 1.25>1.2

8、ROUND_UNNECESSARY

断言请求的操作具有精确的结果，因此不需要舍入。

如果对获得精确结果的操作指定此舍入模式，则抛出ArithmeticException。
--------------------- 
作者：mkl34367803 
来源：CSDN 
原文：https://blog.csdn.net/u010523770/article/details/53068809 
版权声明：本文为博主原创文章，转载请附上博文链接！