评分卡模型工作流程

评分卡模型的工作流程主要分为以下几个步骤：

一、模型构建
假设模型训练集的观察点（即客户的申请时间段）为2014-01到2014-03,那么这个模型的观察期（这里我们假定为三年）为2011-01到2014-01,模型的表现期（这里我们假定为一年）为2014-03到2015-03。

对照上面的模型构建的时间来，我们来建立测试集，假定其测试集观察点（即客户的申请时间段）为（2015-04),同理可得观察期，和表现期真实的违约或者逾期与否。这时把模型放在这个测试集上进行测试看看效果如何。这里需要注意训练集和测试集上用户在表现期的表现如何都是基于一个已经发生的时间段上。

二、数据预处理

1. 数据格式处理
   <1>利率——带%的百分比，需要转化成浮点数
   <2>日期——Nov17, 需要转化为Python的时间
   <3>工作年限——<1 year 转化为0，>10 years 转化成11
   2.文本类数据格式处理
   <1>主题提取（NPL） 缺点：NPL的模型较为复杂，且需要足够多的训练样本
   <2>编码 缺点：信息丢失很高

三、特征构造
1.常用特征衍生
<1>计数：过去1年内申请贷款的总次数
<2>求和：过去1年内的网店消费总额
<3>比例：贷款申请额度的年收入占比
<4>时间差：第一次开户距今时长
<5>波动率：过去3年内每份工作的时间的标准差

2.特征分箱（优势：可将缺失作为独立的一个箱带入模型，将所有变量变换到相似的尺度上）
<1>监督式分箱法
Best-KS 让分箱后组别的分布差异最大化
步骤：1.排序 X=X1,X2,…,Xk
2.计算每一点的KS值
3.选取最大的KS对应的特征值Xm,将X分为Xi<=Xm与Xi>Xm 两部分， 对于每一部分，重复2-3，直至满足终止条件之一
终止条件：1.下一步分箱后，最小的箱的占比低于设定的阈值（常用0.05）
2.下一步分箱后，该箱对应的y类别全部为0或者1
3.下一步分箱后，bad rate不单调

卡方分箱法
步骤：1.初始化。根据要离散的属性对实例进行排序：每个实例属于一个区间
2.合并区间。计算每一对相邻区间的卡方值，将卡方值最小的一对区间合并
卡方阈值的确定，根据显著性水平和自由度得到卡方值
阈值的意义：类别和属性独立时，有90%的可能性，计算得到的卡方值会小于4.6（自由度为2，则90%置信度，即10%显著性水平下，卡方的值为4.6），这样大于阈值的卡方值就说明属性和类不是相互独立的，不能合并。如果阈值选的大，区间合并就会进行很多次，离散后的区间数量少，区间大。
也可不考虑卡方阈值，考虑最小区间数或者最大区间数，指定区间数量的上限和下限
<2>无监督分箱法（等距划分，等频划分）
3.WOE编码
需保证每箱中同时包含好，坏两个类别
WOEi=log[(Gi/Gtotal)/(Bi/Btotal)]

四、特征选择
1.变量挑选的依据：
<1>带约束：LASSO
<2>特征重要性：随机森林
<3>模型拟合优度和复杂度：基于AIC的逐步回归
<4>Information Value IV=(Gi/G-Bi/B)*WOE
目标变量只能是二分类，过高IV存在风险
小于等于0.02 没有预测性，不可用；0.02-0.1弱预测性；0.2+ 高预测性
2.单变量分析
3.多变量分析（两两相关性，相关性高时选IV高的或者分箱均衡的，用VIF(variance inflation factor)方差膨胀因子衡量）
VIF=1/(1-Ri方) 当某个变量的VIF超过10，需要逐一剔除解释变量。当剔除掉Xk时发现VIF低于10，从Xk,Xi中剔除IV较低的一个
VIF的取值大于1。VIF值越接近于1，多重共线性越轻

五、模型
1.逻辑回归 变量挑选：随机森林（将特征按照重要性从高到低排列，选取前n个特征）
评分卡开发的常用模型
Logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。 [1]
logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。 [1]

优点: 简单,稳定,可解释,技术成熟,易于监测和部署
缺点:准确度不高

2.决策树

优点: 对数据质量要求低,易解释
缺点:准确度不高

3.组合模型

优点: 准确度高,不易过拟合
缺点:不易解释;部署困难;计算量大

六、评分卡模型的评价标准
1.区分度
 <1>好，坏人群的分数或违约概率的分布差异 KS >0.3:好； 0.2-0.3 可用；0-0.2较差； <0 评分与好坏程度相悖，模型错误。 KS缺陷：只能表示区分度最好的分数的区分度，不能衡量其它分数
<2>好，坏人群的分数或违约概率的距离 Divergence Divergence=(good均值 - bad均值)^2/[1/2*(Var good+Var bad)] Divergence越大，两类样本的距离越大，差异越大
<3>好，坏人群浓度的差异 Gini

2.准确度
<1>ROC曲线 纵坐标为true positive rate,横坐标为false positive rate
<2>AUC ROC曲线下的面积，常介于0.5和1之间，值越大越好。 >0.7 有很强的区分度； 0.6-0.7 有一定的区分度；0.5-0.6 有较弱的区分度； 低于0.5 区分度弱于随机猜测
<3>AR(Accuracy Ratio) 衡量分数预测能力的指标 ,需要一个完整的表现期。看看这个模型能不能把坏样本很好的区分处理。其取值位于-1~1之间。具有滞后性。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
如果我们今天用AR来监控模型的好坏，那么只能是监控模型在一年（这里假定表现期为一年）之前的数据上表现的好坏。

先把样本按分数由低到高排序，Ｘ轴是总样本的累积比例，Ｙ轴是坏样本占总的坏样本的累积比例。AR就是等于模型在随机模型之上的面积除以理想模型在随机模型之上的面积。计算中可以用梯形近似逼近曲线下面积来计算，AR越高说明模型区分效果越好。

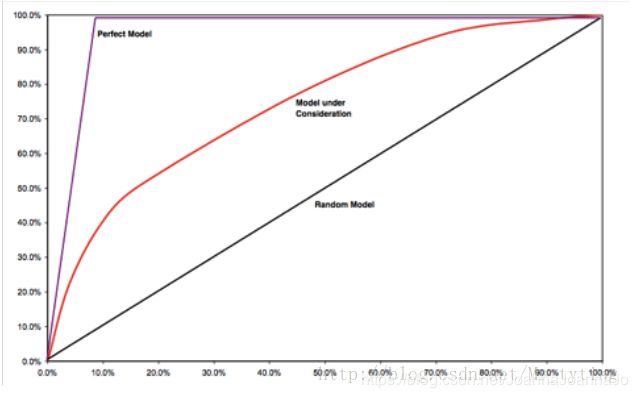
下图公式中Xk,Yk代表分数的第Ｋ个分位点对应的累积总样本及相应的坏样本的比例。设总的坏样本的比例为Bo，令（Ｘk,Yｋ)=(0,0)

3.稳定性
<1>PSI Population Stability Index 衡量分数稳定性的指标，通常要求低于25% 。 PSI越小，分数分布变化越小

PSI( Population Stablility Index)

衡量分数稳定性的指标

按分数对人群进行分组，令Ｒi是现在样本中第ｉ组占总样本的百分比，Bi是一段时间后第ｉ个分组占总样本的百分比。PSI取值越小说明分数的分布随时间变化越小。

<2>Kendall’s Tau

正确有效的评分卡模型中，低分数的实际逾期率应该严格大于高分段的实际逾期率。我们将分数从低到高划分为１０组，每组的实际逾期率记做r1,r2,r3,…,r10。对所有的(ri,rj)的组合，如果有ri< rj且i< j，或者ri> rj且i> j，则记做一个discordant pair，否则记做concordant pair。其计算公式如下：

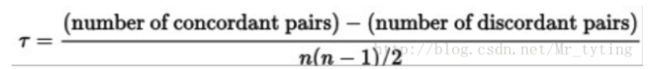
Kendall’s Tau越接近１或者等于１，说明逾期率在分数上的单调下降性越明显，反之说明分数变化与逾期率的变化的一致性得不到保证。

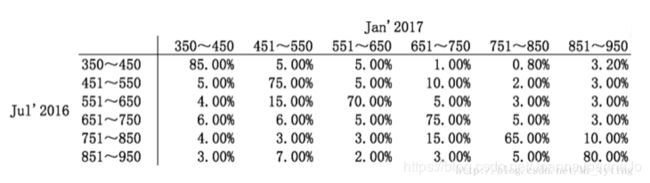
<3>Migration Matrix

迁移矩阵是衡量分数矩阵的指标，对相同的人群，观察在相邻两次监控日期（一周）分数的迁移变化。迁移矩阵中元素Mjk代表上次监控日期分数在第ｊ组中的人群在当前迁移到第ｋ组的概率。实际计算中可把分数平均分成10组，计算这10组之间的迁移矩阵。

七、评分卡分数的计算
Score=Base Point+PDO/ln2*(-y)
其中 y=logit§=log(p/(1-p))
p: 违约概率
Base Point:基准分，无实际意义
PDO: Point to Double Odds,好坏比每升高一倍，分数升高PDO个单位

下面就来讲解一下评分卡具体的计算方法：
定义 odds= p/(1−p) （胜率公式）
评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义。公式如下：
scoretotal=A+B∗In(odds)
设定比率为θ0的特定点分值为P0，比率为2θ0的点的分值为P0+PDD,带入上式就可以很方便的求出A和B值。

一般来说我们会用Logistic Regression来表征对于P值的估计，公式如下：
P= 1/(1+e ^−θ T *x)
则有odds=In(p/(1−p))=θTx （logit函数）
故有scoretotal=A+B∗(θTx)=A+B∗(w0+w1x1+…wnxn)=(A+B∗w0)+B∗w1x1+…+B∗wnxn
其中A和B在之前的布置中已经计算出来了，xn是特征数据的WOE编码
这样来了一个用户申请之后，就可以根据评分卡得出最终用户的信用得分，进而决定是否是否接受该用户的借贷申请。
需要注意的是，上面这种做法只是一种经典的做法，但不是唯一的做法。比方说对于同一变量x1，它的不同的WOE可以对应不同的w系数。同时不一定采用WOE编码（只不过这种编码方式在信贷评分场景中更常用），还有很多种其他的编码方式可以选择，比方说one-hot编码等。

同时可以扩展的是，不一定要针对全部的用户用一张评分卡模型，可以按照类似决策树的方式对用户进行分类，针对每一个子类的用户生成一份具有针对性的评分卡模型

还有最后一个额外的扩展点，有时候往往因为业务的需要，我们需要对这些系数w1,wn
的大小做一个限制（往往业务专家希望对应WOE值大的变量的变量所对应的系数w也要大一些），这就要求在进行模型训练的时候采用相应的策略：

无约束的优化算法：SGD，Newton Method，L-BFGS
有约束的优化算法：Barrier Method，SQP(Active Set Method)