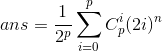E.Counting Sequences II (2019上海网络赛)指数生成函数

https://nanti.jisuanke.com/t/41413

题意：给出一个1*n的方格，和1-m的数，每一个数有无限多吧，要求，把方格填满，但不过偶数必须出现偶数次，求方案数。

做法：首先，我当时不知道这是一道生成函数，给一个学习生成函数的博客https://blog.csdn.net/wu_tongtong/article/details/78854572

这道题如果用组合数学的纯推，我想很难吧。。。。

如果在你看了生成函数后，就知道怎么做了。

首选对于每一个偶数：

对于每一个奇数：

我假设在1-m范围内偶数的个数为p，奇数的个数q

所以总的生成函数：

我们假设m为一个偶数那么奇数和偶数个数相等

因此结合二项式定理：

而我们知道 前面的系数就是我们要的组合方案数。因此可以得到我们的答案：

上面就是对应的当m为偶数时的答案。

对于当m为奇数时，也很简单，q就比p大1，最后外面就多了一个e^x

这里就不推导了。直接给出答案：

//#include "bits/stdc++.h"
#include
#include

using namespace std;
typedef long long ll;
const ll mod = 1000000000 + 7;
ll quick(ll a, ll n) {
    ll ans = 1;
    for (; n; n >>= 1, a = a * a % mod)
        if (n & 1) ans = ans * a % mod;
    return ans;
}
ll fac[100010], inv[100010];
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    fac[0] = inv[0] = 1;
    for (int i = 1; i <= 100001; i++) {
        fac[i] = fac[i - 1] * 1ll * i % mod;
    }
    inv[100001] = quick(fac[100001], mod - 2);
    for (int i = 100000; i >= 1; i--) {
        inv[i] = inv[i + 1] * (i + 1) % mod;
    }

    ll n, m;
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m;
        int p = m / 2;
        ll invp = quick(2, p);
        invp = quick(invp, mod - 2);
        ll sum = 0;
        for (int i = 0; i <= p; i++) {
            ll C = fac[p] * inv[i] % mod * inv[p - i] % mod;
            sum += C * quick(2 * i + (m & 1), n) % mod;
            sum %= mod;
        }
        cout << sum * invp % mod << endl;
    }
    return 0;
}