字符串匹配算法-KMP
KMP算法是一种高效的字符串匹配算法,显然OI有用,但是网上和书上(AKA算导)讲的总是看不懂,KZ相信是因为KZ个人能力不够,但是通过老师的讲解理解后,在这里尝试用一种更好理解的方式讲解KMP算法。同时,KZ将描述一种个人认为更适合OI的实现方法。
KMP原理
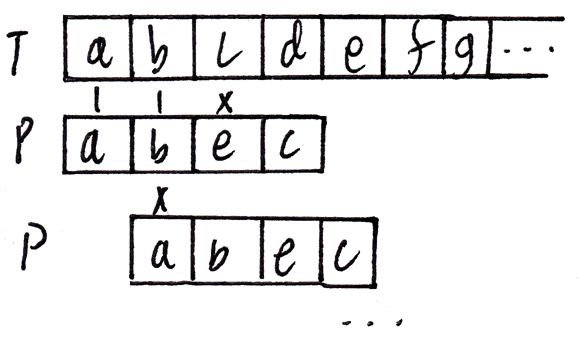
最暴力的字符串匹配算法无非是依次比对文本串T和模式串P,失配的话把P向后移动一格,如下图。
上述算法把时间浪费在了反复前一部分已经匹配了的字符上,而KMP算法则正是优化了这一点,从而更有效率。
如下图:
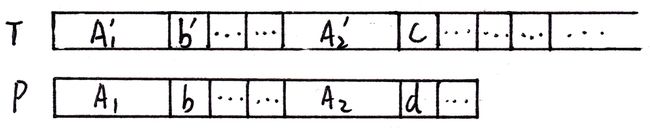
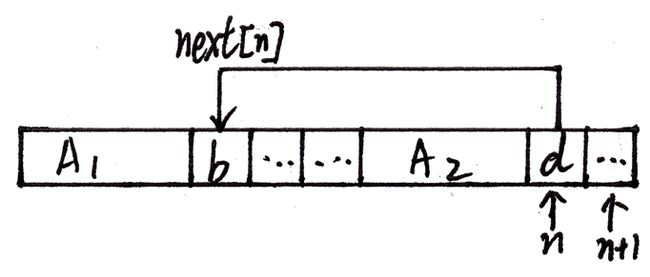
上图:串A1 == A2 == A'1 == A'2 , b == b'
当匹配上述两个串时,前面全部匹配,直到c与d失配。若不仅将P向右滑动一格,而是更多:
显然此时省去了比较A1与A'1的时间,这就是KMP算法高效的关键所在。
KMP通过适当的滑动,使得P的最长前缀(A1),与T中 已经匹配成功的串 的最长后缀(A'2)相匹配,因为这一部分已经与P中失配位(d)前面的部分相匹配(A'2 == A2),所以KMP仅通过对P的预处理,即可得出失配时滑动的方案。
预处理时间为O(|P|),匹配时间为O(|T|)。
滑动方案计算
KMP的原理很好理解,唯一稍有思维难度的是对于滑动方案的计算,这里使用next[]的方法来解决。
此方法以及别的实现方法原理相同,仅在细节上有所区别(如数组下标从哪个开始用),KZ认为next[]方法最便于理解和书写(AKA适合OI)。
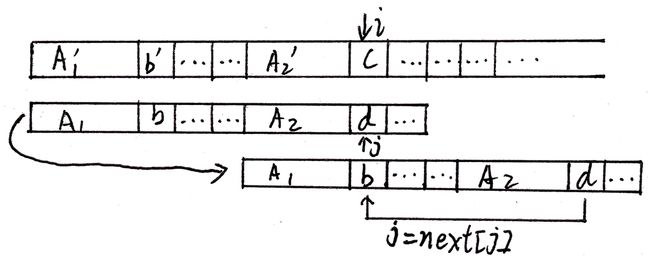
next[j]表示当在P[j]失配时,指针j跳转到next[j],如下图。
即P[next[j]]以前的串(A1)(P的最长前缀),与P[j]以前的串的最长后缀(A2)相等(A1 == A2)。
接下来讨论具体的计算方式:
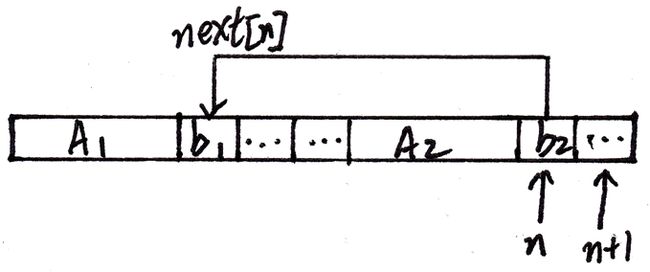
首先明确,next[n+1]由next[n->0]推出。
当P[n] == P[next[n]]时,如下图:
显然根据next[]的定义,存在A1 == A2,此时又有b1 == b2,则A1+b1 == A2+b2,两个子串相等,所以next[n+1] = next[n]+1。
即P[next[n]+1]以前的串(A1+b2)(P的最长前缀),与P[n+1]以前的串的最长后缀(A2+b2)相等(A1+b1 == A2+b2)。
注意,之所以next[n]+1,是为了满足“以前的串”这个要求。
那么当P[n] != P[next[n]]时,
诶?存在P[n] != P[next[n]]的情况吗?是存在的!
因为next[]的定义,使得相等的串在P[n]与P[next[n]]的前面,所以这两者不一定相等,况且在“当P[n] == P[next[n]]时”处理的时候,并没有判断P[next[n]+1]于P[n+1]是否相等。如果没看懂,或许可以在看完全文之后回过来看KZ到底说了什么。
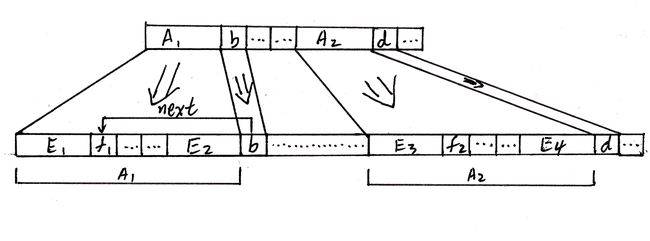
总之,当P[n] != P[next[n]]时,如下图:
A1+b已经无法与A2+d匹配,而A2又不是合法的后缀,所以KZ拆开A1,A2来看看:
因为A1 == A2,所以存在E1 == E3,f1 == f2,E2 == E4,
同时由next[]的定义,存在E1 == E2,所以得到E1 == E4。
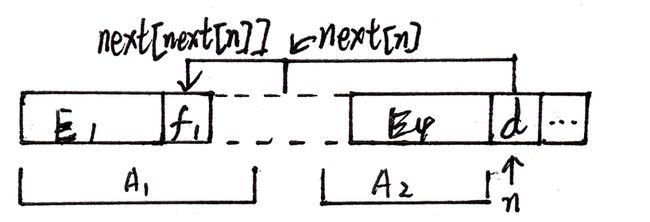
如图:
这样看起来就和之前的情况相似了,事实上是的,反回去判断P[next[next[n]]]与P[n]是否相等即可,重复上述过程。
如此往复一直到找到相等的,或者跑到了P[0],那么此时的next[n+1]就只能是0,可理解为两个空串相等了。
样例代码
void kmpNext(char P[], int Psize, int next[]) {
int k, i;
k=-1; i=0; next[0]=-1;//初始化,-1表示跳到头部
while(jint kmpMatch(char T[], int Tsize, char P[], int Psize, int next[]) {
int i=0, j=0;
while (i=Psize)
return i-Psize+1;//返回第一个匹配的头部下标
else
return -1;//匹配失败
}