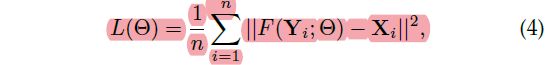Image Super-Resolution Using Deep Convolutional Networks (SRCNN)

0.Abstract

作者提出一种深度学习的方法用于解决超分辨率问题(super-resolution, SR)，具体的是，使用CNN来拟合低分辨率图像和高分辨率图像的映射，这是一种端到端的方法；而且传统的基于稀疏编码的SR方法（the sparse-coding-based method）也是能被看作CNN的；重要是的，这个CNN是个轻量级模型，能在实际应用快速的同时，保证达到图像重建的当前先进水平(state-of-art)。

 

1.Introduction

解决SR问题的大概都是基于例子的策略（example-based strategy），主要有两种思路：

a.利用同一图像的内部相似性；

b.从外部低分辨率和高分辨率示例图片对中学习映射函数；

基于稀疏编码的SR方法就是学习映射函数的一种代表方法，该方法包括以下几步：

a.从输入图片中密集地进行采样形成大量的重叠的patch，并且对这些patch进行预处理（例如减去均值、标准化）；

b.使用一个低分辨率的字典（low-resolution dictionary）对patch进行编码；

c.使用一个高分辨率的字典（high-resolution dictionary）对b的输出进行编码，用来构建高分辨率的patch；

d.将重叠的patch进行聚合产生最终的输出；

作者提出的Super-Resolution Convolutional Networks（SRCN）具有以下几个优点：

a.结构简单但是准确率很高；

b.卷积核数和层数适中，在实际的及时应用中，即使使用CPU也能得到很快的相应速度；

 

2.Related Work

对于大部分的SR算法都是关注灰度图片或单通道的图片；至于彩色图片，这些传统的算法（例如）都是先将彩色图片（RGB）转换到不同的色彩空间（例如YCbCr、YUV），再在亮度通道上使用SR算法；

 

3.Convolutional Neural Networks for Super-Resolution

a.构想：

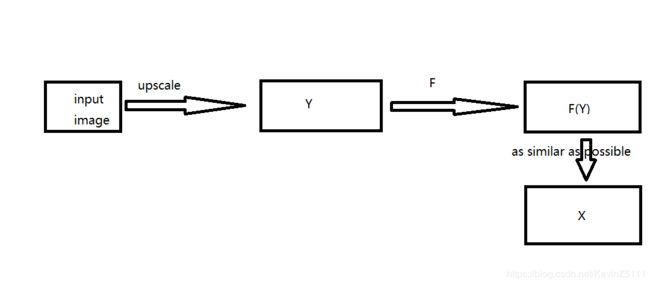
首先将输入图片使用双三次插值法（bicubic interpolation）放大到想要的大小，这是我们唯一需要做的预处理，并且我们把经过预处理后的图片记作Y。我们的目标是学习出一个映射F，使得F(Y)和真实高分辨率图片X尽可能的相似。如图1所示：

图1

我们想要学习的这个函数F，其实可以分解成三部分操作：

i.Patch extraction and representation：从Y中提取出patch，然后将每个patch映射成一个高维向量，并且这些向量可以组成一个featuremap；

ii.Non-linear mapping:将上一步得到的高维向量经过非线性变换转换为另一个高维向量，这些高维向量也能得到一个featuremap；

iii.Reconstruction:将上一步生成的高维向量合成最终的高分辨率图片输出；

具体的操作如下：

Patch extraction and representation:这个操作等同于使用带有偏置的卷积核在图片上进行卷积运算，我们可以写成：

其中W1、B1分别表示为卷积核和偏置，*表示卷积运算；W1对应于n1个大小为c×f1×f1的卷积核(c表示输入图片的通道数)

Non-linear mapping：这个操作对应于使用n2个大小为1×1的卷积核进行运算，当然卷积核的大小是可以改变的，使用更大的卷积核会有更好的泛化效果，我们可以写成：

其中W2对应于n2个大小为n1×f2×f2的卷积核。虽然增加更多的卷积层能增加非线性，但是会使得模型复杂度增加，从而需要更多的训练时间。

Reconstruction：这个操作可以看成在featuremap上使用预先定义的卷积核进行averaging的过程，这是一个线性过程：

其中W3对应于c个大小为n2×f3×f3的卷积核

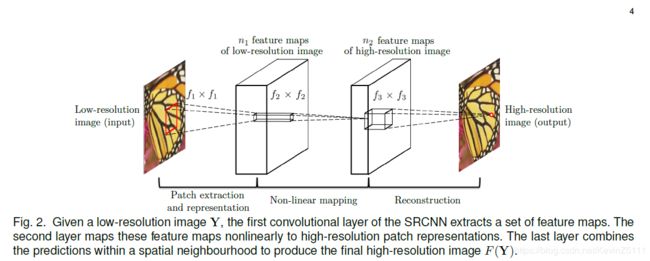
以上的操作如图2所示。

图2

b.和基于稀疏编码的SR方法的关系：

传统的基于稀疏编码的SR方法可以被看成一个卷积神经网络，如图3所示：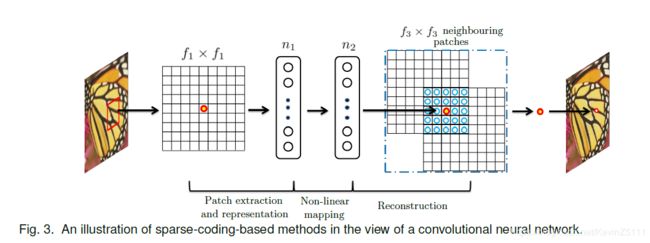

图3

具体来说是：

在基于稀疏编码的SR方法模型中，我们可以把f1×f1低分辨率的patch看成是从输入图片提取出来的，然后稀疏编码求解程序将patch投影到一个字典上，如果这个字典的大小为n1，那么相当于在输入图片上使用n1个大小f1×f1的卷积核进行卷积运算，如图3的左半部分所示。稀疏编码求解程序会迭代的处理n1维度的向量，从而得到一个n2维度的向量，一般来说n1、n2是相等的，这个时候稀疏编码求解程序起的作用就是一个大小为1×1的非线性映射运算符，如图3的中间部分所示。然后再对n2维度的向量投影到另一个字典空间目的是产生高分辨率的patch，重叠部分的patch会进行平均操作，如图3的右半部分所示。

在SRCNN中，以上的低分辨率字典、高分辨率字典、非线性映射、减去均值和平均化的操作都包括在需要优化的卷积核里了，所以说该模型是一个包括所有操作的端到端的映射。而且之所以SRCNN的表现更好是因为SRCNN使用更多的像素信息用于图像重构。例如当我们设置f1=9,f2=1,f3=5,n1=64,n2=32时，高分辨率像素使用了(9+5-1)^2=169个像素的信息，而传统的方法只使用了(5+5-1)^2=81个像素的信息。

c.训练：

该模型的参数有：W1,W2,W3,B1,B2,B3。给定一组高分辨率图片Xi以及对应低分辨率图片Yi，我们使用MSE作为损失函数：

其中n表示训练样本的数量，使用MSE作为损失函数会使得PSNR值变得很高，损失函数使用SGD进行优化，参数的更新过程如下所示：

参数Wi使用均值为0标准差为0.001的高斯分布进行初始化，参数Bi初始化为0，前两层的学习率为10^-4，最后一层的学习率为10^-5，而且作者发现在最后一层使用小的学习率对于SRCNN收敛很重要。为了避免在训练时边界影响，所有CNN都采用no padding的策略

 

4.Experiments

a.训练集大小对实验结果的影响：

作者使用了一个24800大小的训练集和一个5百万大小的训练集，在相同结构的SRCNN（f1=9,f2=1,f3=5,n1=64,n2=32）上进行训练，而且使用基于稀疏编码的SR方法作为baseline，最后的结果如图4所示：

由此作者得出以下结论：

使用大型的训练集可能对SRCNN的表现有提升，但是训练集大小的影响不大，不像如分类问题那么明显；

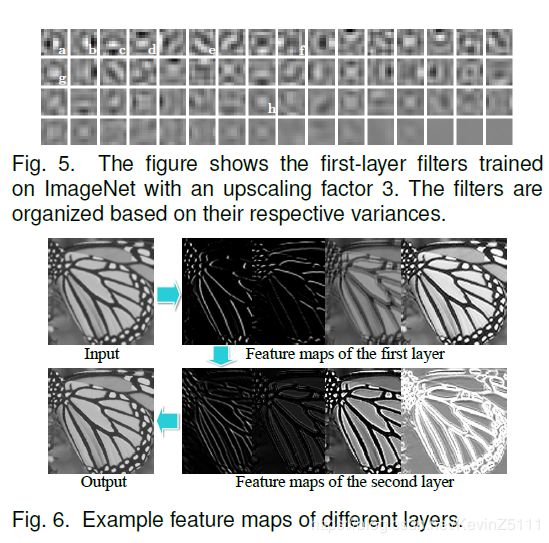
b.SR中已学习的卷积核：

 从图中可以看出：卷积核g、h类似于拉普拉斯核或高斯核，卷积核a-e就像不同方向的边缘检测器，卷积核f类似于一个纹理提取器。于是作者得出以下结论：

第一层的featuremap中包括不同的结构，例如不同方向上的边缘；第二层主要是光照强度的不同

c.模型大小和模型表现的折衷:

将网络参数设置成f1=9,f2=1,f3=5,n1=64,n2=32并将该网络称为basic network。

i.卷积核的数量：

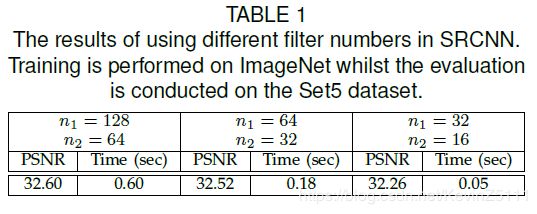
通常来说，如果我们使用更多的卷积核网络的性能会有提升。为了证明这点是否适用于SRCNN，首先设置不同的参数：第一组n1=128，n2=64；第二组n1=32，n2=16；都在相同的训练集和测试集上，得到的结果如下表所示：

作者得出了以下结论：

通过增加卷积核的数量能得到更好的性能；

但是卷积核越多，图像重构的时间越长；

ii.卷积核大小：

我们将f1=9,f2=1,f3=5记作9-1-5。

首先，我们固定第二层卷积核大小为f2=1，并设置f1=11,f3=7(11-1-7)的到的结果为32.57dB，与(9-1-5)网络的结果为32.52dB。于是得到结论：适当的增大卷积核大小能获得更多的结构信息，所以会得到更好的结果。

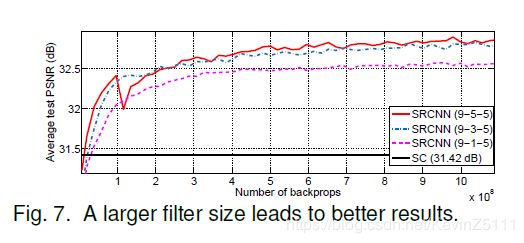
其次，我们固定f1=9，f3=5，增大第二层卷积核的大小:f2=3（9-3-5），f2=5（9-5-5）。最后的结果如下图所示：

得出以下的结论：

增大第二层卷积核的大小能显著提升性能，这说明利用周围的信息在映射阶段是有益的；

但是增大第二层卷积核大小会使得模型复杂度、以及降低了部署的时间；

 

iii.层的数量

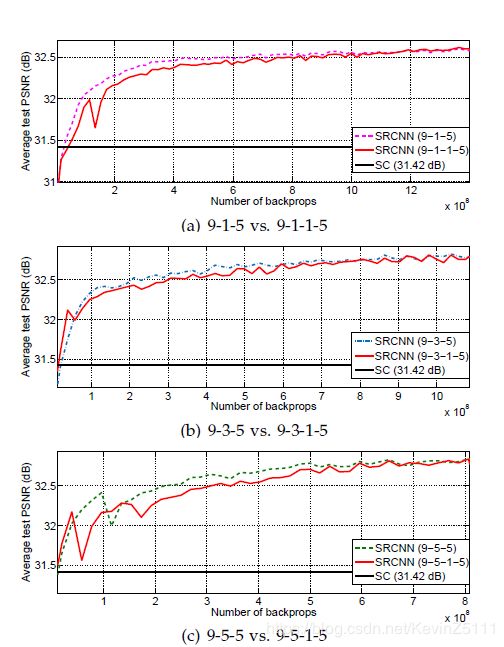
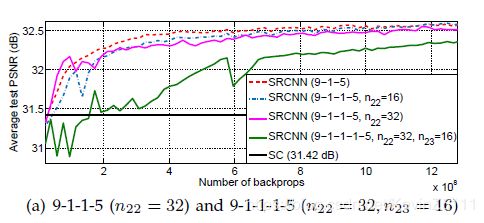
我们尝试着增加SRCNN的深度，增加一层n22=16，f22=1，于是可以得到(9-1-1-5)、（9-3-1-5）、（9-5-1-5），添加的这一层的初始化参数和学习率和第二层一样。得到如下图的结果：

由此作者得出了以下结论：

四层网络比三层网络的收敛速度慢，但是给定足够的时间，四层网络最后也会追上三层网络的；

但是并不像图像分类问题上网络深度越深效果越好，SR问题并不能看出网络深度对网络表现的影响，而且随着网络深度的增加可能还会导致性能的下降；

导致以上结论的原因可能是SRCNN没有池化层和全连接层，所以它对初始化参数和学习率很敏感。当模型层数增加时，我们很难保证找到一组合适的学习率使得其收敛，即使模型收敛了，也可能陷入一个不好的局部最小值，并且经过足够的训练时间，已学习的卷积核的多样性会变少。而且在图像分类领域，不适当的增加模型深度也会使得准确率的下降或退化。

d.与state-of-art进行比较：

 

5.Conclusion

作者提出了基于稀疏编码的卷积方法，并将其实现为一个深度神经网络SRCNN，能够学习端到端的低分辨率图片到高分辨率图片的映射，而且这是个轻量级的结构，有着超越其他state-of-art方法的表现