论文笔记-损失函数之SSIM

损失函数用来鼓励和抑制某些行为。
在深度学习中，如果是分类问题，则可以用交叉熵，softmax,SVM等损失函数。如果是回归问题，则代价函数普遍采用L2，或者L1。
由于L2（即用真值和预测值的欧氏距离）是一个非凸形式且可导。。但L2的使用前提是噪声高斯分布的。它抑制大的误差，但对小的误差却很能容忍。比如L2能很好地复现边缘，但却无法很好地消除那些小的噪声。
最重要的，L2和人类的视觉系统（human visual system (HVS)）很不一样。HVS对局部信息很敏感，对光照，颜色变化很敏感。而人类制造的相机，其感光能力是以HVS为努力方向的。
结构相似性指数（structural similarity index，SSIM）和HVS一样，对局部结构变化很敏感，而且可导。即使对图片进行白噪声，对比度增强，mean-shifted处理，SSIM也不会变化太多。

先写两篇文章的简略笔记

1.论文一

Image Quality Assessment: From Error Visibility to Structural Similarity

当对一幅图片进行有损压缩，或者一幅图片有了噪声、畸变（distortion）等。我们人可以分辨出这两幅图大概率还是同一幅图，但如何有效地衡量他们的相似性呢？
为了抵消普通的L2距离（Mean Square Error,MSE）无法衡量图片的结构相似性的缺陷，这篇文章提出了SSIM这种structure similarity的方法来做最后变化后的图片与变化前的结构相似性。

(各类相机的宗旨也是提供给更接近人眼感知系统(human vision system,HVS)的感知能力)
人眼对光照不敏感，但对局部（图像不同部分）光照的变化敏感。对灰度不敏感但对各部分灰度的相对变化程度敏感（对比度变化）。以及对整个很大局部的结构敏感。基于以上认知，作者最后提出的：

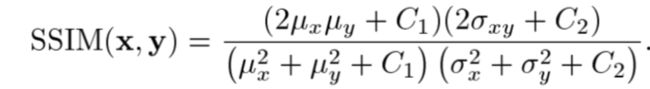
对于两个DxD的图像块，他们的SSIM始终小于1；1表示完全相似。其中 ux,uy 是图像块所有像素的平均值， σxσy 是图像像素值的方差；
SSIM实际上是三个比较部分的乘积：
图像照明度比较部分：

图像对比度比较部分

图像结构比较部分：

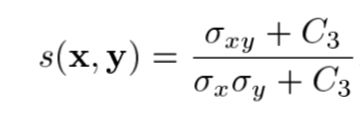
其中

SSIM相当于将数据进行归一化后，分别计算图像块照明度（图像块的均值），对比度（图像块的方差）和归一化后的像素向量这三者相似度，并将三者相乘。
SSIM计算某个window的相似度（比如11X11),然后将所有window的相似度做一个平均（得到MSSIM）作为整张图片的相速度。

照明度部分对各个部分明度差异更敏感，对比度部分对低对比度部分更加敏感。
作者在计算每个图像块之前，会先对要计算的window进行一个高斯模糊(即点乘上一个与window同等大小的高斯分布的权重mask)

2.论文2

Loss Functions for Neural Networks for Image Processing
之前会用L2,Pek signal-to-Noise Ratio , PSNR，等作为损失函数.
L1,L2,SSIM,MS-SSIM,MS-SSIM+L1
目前神经网络已经大量用于降噪，降模糊，提升分辨率，去马赛克等工作中。但这些工作中大家往往执着于调整网络结构，而非代价函数。

作者发现即使在L2表现良好的情况下，L1,SSIM等能获得更好的表现。而且令人惊讶的是L1表现与SSIM差别不大。因此作者提出将“combines the advantages of l1 and MS-SSIM ”
即最终：

顺便介绍：MS-SSIM是图像进行缩放之后形成金字塔的SSIM：

其中 α=0.84

实验阶段，作者分别作了打马赛克和去马赛克、提升分辨率、jpeg压缩后的图片失真度检测四个人物分别测试这种混合的代价函数的，结果优于L2.

最后作者讨论了L2收敛性问题和高斯模糊的程度对最后结果的影响。
作者发现L2的收敛特性：结合使用L1,L2比单独使用L1或L2表现更好，因为他们的收敛区间可能不同。比如L2的局部最小值可能很多，阻止了它进一步下降；而更平滑(局部最小值相对更少)的L1更容易获得更好的局部最小值：如图

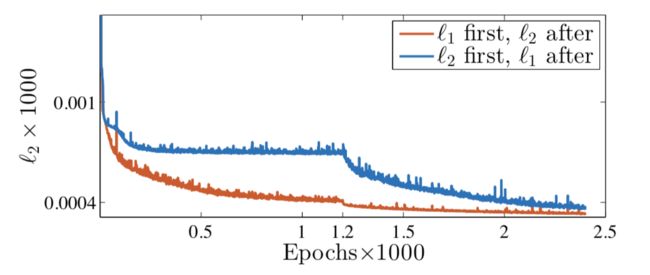
这也同时让我回忆起现在很多网络使用L1,L2混合的模式。

当高斯模糊的mask的高斯核很小时，边缘保存很好，但平缓地带的效果较差。高斯核较大时正相反。