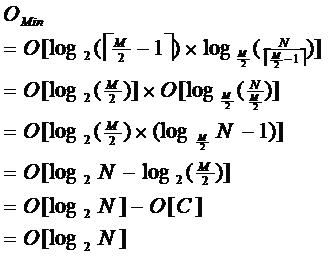oracle关于索引
一. 说说你对索引的认识(索引的结构、对dml影响、对查询影响、为什么提高查询性能)
索引有B-TREE、BIT、CLUSTER等类型。ORACLE使用了一个复杂的自平衡B-tree结构;通常来说,在表上建立恰当的索引,查询时会改进查询性能。但在进行插入、删除、修改时,同时会进行索引的修改,在性能上有一定的影响。有索引且查询条件能使用索引时,数据库会先度取索引,根据索引内容和查询条件,查询出ROWID,再根据ROWID取出需要的数据。由于索引内容通常比全表内容要少很多,因此通过先读索引,能减少I/O,提高查询性能。
二. 使用索引查询一定能提高查询的性能吗?为什么
通常,通过索引查询数据比全表扫描要快.但是我们也必须注意到它的代价.
索引需要空间来存储,也需要定期维护, 每当有记录在表中增减或索引列被修改时,索引本身也会被修改. 这意味着每条记录的INSERT,DELETE,UPDATE将为此多付出4,5 次的磁盘I/O. 因为索引需要额外的存储空间和处理,那些不必要的索引反而会使查询反应时间变慢.使用索引查询不一定能提高查询性能,索引范围查询(INDEX RANGE SCAN)适用于两种情况:
基于一个范围的检索,一般查询返回结果集小于表中记录数的30%宜采用;
基于非唯一性索引的检索
索引就是为了提高查询性能而存在的,如果在查询中索引没有提高性能,只能说是用错了索引,或者讲是场合不同。
关于B-tree结构:
B- 树
是一种多路搜索树(并不是二叉的):
1. 定义任意非叶子结点最多只有 M 个儿 子;且 M>2 ;
2. 根结点的儿子数为 [2, M] ;
3. 除根结点以外的非叶子结点的儿子数为 [M/2, M] ;
4. 每个结点存放至少 M/2-1 (取 上整)和至多 M-1 个关键字;(至少 2 个关键 字)
5. 非叶子结点的关键字个数 = 指向儿 子的指针个数 -1 ;
6. 非叶子结点的关键字: K[1], K[2], …, K[M-1] ;且 K[i] < K[i+1] ;
7. 非叶子结点的指针: P[1], P[2], …, P[M] ;其中 P[1] 指向关键字小于 K[1] 的子树, P[M] 指向关键字大于 K[M-1] 的子树,其它 P[i] 指 向关键字属于 (K[i-1], K[i]) 的子树;
8. 所有叶子结点位于同一层;
如:( M=3 )
B- 树的搜索,从根 结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经 是叶子结点;
B- 树的特性:
1. 关键字集合分布在整颗树中;
2. 任何一个关键字出现且只出现在一个结点中;
3. 搜索有可能在非叶子结点结束;
4. 其搜索性能等价于在关键字全集内做一次二分查找;
5. 自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有 M/2 个儿子,确保了结点的至少利用率,其最底搜索性能为:
其中, M 为设定的非叶子结点最多子树个 数, N 为关键字总数;
所以 B- 树的性能总是等价于二分查找 (与 M 值无关),也就没有 B 树平衡 的问题;
由于 M/2 的限制,在插入结点时,如果 结点已满,需要将结点分裂为两个各占 M/2 的结点;删除结点时,需将两个不足 M/2 的 兄弟结点合并;