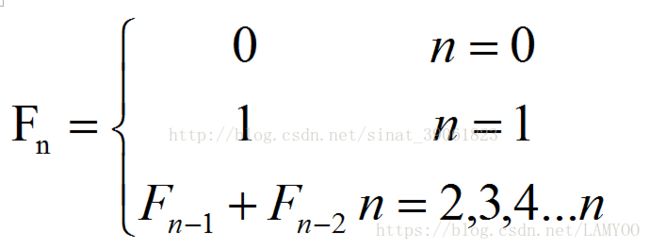递归算法小结(数的阶乘、斐波那契和汉诺塔问题)
递归是一项重要的编程技术,它让函数可以从函数体内部调用自身。递归通常把一个大型复杂的问题层层简化为一个,与原问题相似的规模较小的问题来求解,使用递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,这样就大大地减少了程序的代码量。但是使用递归的时候需要消耗较多的栈空间,所以递归次数过多容易造成栈溢出等。在堆栈尺寸受到限制的时候 ,一般需要避免使用递归。
1.
什么是递归
递归指的是函数在定义中直接或间接使用函数自身的方法。因此递归可分为直接递归和间接递归:
(1)直接递归:递归函数直接调用该函数本身。
(2)间接递归:一个递归函数调用另一个递归函数,再从另一个递归函数调用回原来的递归函数。
2.
递归的条件
(1)可以反复执行的递归过程。
(2)有一个跳出递归过程的条件,也就是不能无限递归。
3.递归应用1--数的阶乘
用递归实现一个给定数的阶乘。
递归C语言实现:
#include
double factorial(unsigned int i);
int main(){
unsigned int i = 5;
printf("%d 的阶乘为 %lf\n", i, factorial(i));
return 0;
}
double factorial(unsigned int i){
if(i <= 1){
return 1;
}
return i * factorial(i - 1);
} 运行结果:
3.递归应用2--斐波那契数列
定义:一个数列的第0项是0,第1项是1,数列后的其他项是前两项数值之和。
含10个元素的斐波那契数列为:
0,1,1,2,3,5,8,13,21,34
递归C语言实现:
#include
int fibonaci(int i);
int main(){
int i;
for(i = 0; i < 10; i++){
printf("%d\t\n", fibonaci(i));
}
return 0;
}
int fibonaci(int i){
if(i == 0){
return 0;
}
if(i == 1){
return 1;
}
return fibonaci(i - 1) + fibonaci(i - 2);
} 
4.
递归应用3——汉诺塔问题(递归应用经典问题,能明白汉诺塔问题,递归就算理解了)
来源(百度百科):汉诺塔(又称河内塔)问题是源于印度的一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
从上易知汉诺塔问题需遵循三个规则:
(1)同一根柱子上从下到上圆盘的直径依次减小。
(2)每一次只能移动一个圆盘。
(3)每次移动只能从最上面的圆盘移动。
解:(1)n == 1
第1次 1号盘 A---->C sum = 1 次
(2) n == 2
第1次 1号盘 A---->B
第2次 2号盘 A---->C
第3次 1号盘 B---->C sum = 3 次
(3)n == 3
第1次 1号盘 A---->C
第2次 2号盘 A---->B
第3次 1号盘 C---->B
第4次 3号盘 A---->C
第5次 1号盘 B---->A
第6次 2号盘 B---->C
第7次 1号盘 A---->C sum = 7 次
不难发现规律:1个圆盘的次数 2的1次方减1
2个圆盘的次数 2的2次方减1
3个圆盘的次数 2的3次方减1
。 。 。 。 。 。
n个圆盘的次数 2的n次方减1
故:移动次数为:2^n - 1
递归C语言实现:
#include
void Move(char x, char y){
printf("%c -> %c\n", x, y);
}
void Hanoi(int n, char one, char two, char three){
if(1 == n){
Move(one, three);
}
else{
Hanoi(n - 1, one, three, two);
Move(one, three);
Hanoi(n - 1, two, one, three);
}
}
int main(){
void Hanoi(int n, char one, char two, char three);
int m;
printf("input the number of disks:");
scanf("%d", &m);
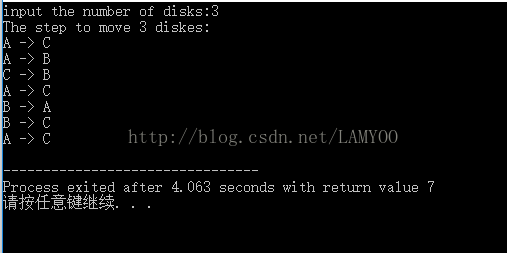
printf("The step to move %d diskes:\n", m);
Hanoi(m, 'A', 'B', 'C');
}
运行结果
: