ADC相关参数之---分辨率和精度(INL和DNL)

       笔者最近在做的一个项目中，用到一片16位的高分辨率的芯片，借此再学习一下由于ADC和DAC的相关知识，以此巩固。

      关于ADC的精度和分辨率将在另外一篇博客讨论，分辨率不等于精度。

     一块精度0.2%（或常说的准确度0.2级）的四位半万用表，测得A点电压1.0000V，B电压1.0005V,可以分出B比A高0.0005V，但A点电压的真实值可能在0.9980~1.0020之间不确定。

       那么,既然数字万用表存在着精度和分辨率两个指标，那么,对于ADC和DAC，除了分辨率以外，也存在精度的指标。模数器件的精度指标是用积分非线性度（Interger NonLiner）即INL值来表示。也有的器件手册用 Linearity error 来表示。他表示了ADC器件在所有的数值点上对应的模拟值，和真实值之间误差最大的那一点的误差值。也就是，输出数值偏离线性最大的距离。单位是LSB（即最低位所表示的量）。

       比如12位ADC：TLC2543，INL值为1LSB。那么，如果基准4.095V，给定数字量1000，输出电压在1V，那么，真实电压值可能分布在0.999~1.001V之间。对于DAC也是类似的。比如DAC7512,INL值为8LSB，那么，如果基准4.095V，给定数字量1000，那么输出电压可能是0.992~1.008V之间。

      下面再说DNL值。理论上说，模数器件相邻量个数据之间，模拟量的差值都是一样的。就相一把疏密均匀的尺子。但实际并不如此。一把分辨率1毫米的尺子，相邻两刻度之间也不可能都是1毫米整。那么，ADC相邻两刻度之间最大的差异就叫差分非线性值（Differencial NonLiner）。DNL值如果大于1，那么这个ADC甚至不能保证是单调的，输入电压增大，在某个点数值反而会减小。这种现象在SAR（逐位比较）型ADC中很常见。 
     举个例子，某12位ADC，INL=8LSB，DNL=3LSB（性能比较差），基准4.095V，测A电压读数1000，测B电压度数1200。那么，可判断B点电压比A点高197~203mV。而不是准确的200mV。对于DAC也是一样的，某DAC的DNL值3LSB。那么，如果数字量增加200，实际电压增加量可能在197~203mV之间。

      很多分辨率相同的ADC，价格却相差很多。除了速度、温度等级等原因之外，就是INL、DNL这两个值的差异了。比如AD574,贵得很，但它的INL值就能做到0.5LSB，这在SAR型ADC中已经很不容易了。换个便宜的2543吧，速度和分辨率都一样，但INL值只有1~1.5LSB，精度下降了3倍。 
     另外，工艺和原理也决定了精度。比如SAR型ADC，由于采用了R-2R或C-2C型结构，使得高权值电阻的一点点误差，将造成末位好几位的误差。在SAR型ADC的2^n点附近，比如128、1024、2048、切换权值点阻，误差是最大的。1024值对应的电压甚至可能会比1023值对应电压要小。这就是很多SAR型器件DNL值会超过1的原因。但SAR型ADC的INL值都很小，因为权值电阻的误差不会累加。 
    和SAR型器件完全相反的是阶梯电阻型模数/数模器件。比如TLC5510、DAC7512等低价模数器件。比如7512，它由4095个电阻串联而成。每个点阻都会有误差，一般电阻误差5%左右，当然不会离谱到100%，更不可能出现负数。因此这类器件的DNL值都很小,保证单调。但是，每个电阻的误差，串联后会累加，因此INL值很大，线性度差。

     这里要提一下双积分ADC，它的原理就能保证线性。比如ICL7135，它在40000字的量程内，能做0.5LSB的INL值（线性度达到1/80000 !!）和0.01LSB的DNL值.这两个指标在7135的10倍价钱内，是不容易被其他模数器件超越的。所以7135这一类双积分ADC特别适合用在数字电压表等需要线性误差非常小的场合。 
     还要特别提一下基准源。基准源是测量精度的重要保证。基准的关键指标是温飘，一般用ppm/K来表示。假设某基准30ppm/K，系统在20~70度之间工作，温度跨度50度，那么，会引起基准电压30*50=1500ppm的漂移，从而带来0.15%的误差。温漂越小的基准源越贵，比如30ppm/K的431，七毛钱；20ppm/K的385，1块5；10ppm/K的MC1403，4块5；1ppm/K的LM399,14元；0.5ppm/K的LM199，130元。 
该死的教科书害了一代学生。在ADC电路中的基准源不能直接接电源VCC，这里要考虑基准电压的稳定度。其中常用的基准源电压可由TL431提供。 
       最后说一下Sigma-Delta型ADC，它比较特殊，对于精度，一般用直接用线性度表示，比如0.0015%.不说差分非线性值，而直接用有效分辨率来表示。此外，Sigma-Delta型ADC还存许多怪脾气，难伺候。 

总结： 
     （1）INL(Interger NonLinear,Linearity error)精度。理解为单值数据误差，对应该点模拟数据由于元器件及结构造成的不能精确测量产生的误差。 
     （2）DNL(Differential NonLinear)差分非线性值。理解为刻度间的差值，即对每个模拟数据按点量化，由于量化产生的误差。 
例子： 
     (1)INL,精度 
     比如12位ADC：假设基准Vref=4.095V,那么1LSB=Vref/2^12=0.001V。如果精度为1LSB，则它的单值测量误差0.001V*1=0.001V,比如测量结果1.000V，实际在1.000+/-0.001V范围。如果精度为8LSB，则他的单值测量误差0.001V*8=0.008V,比如测量结果1.000V，实际在1.000+/-0.008V范围 
(2)DNL，差分非线性值 
     比如12位ADC：假设基准Vref=4.095V,那么1LSB=Vref/2^12=0.001V。不考虑精度，即精度为0LSB。没有单值误差。如果DNL=3LSB=0.001V*3=0.003V假设A实际电压为1.001V,B实际电压为1.003V。理论上A点读数1.001V/1LSB=1001，B点读数1.003V/1LSB=1003，B-A=2,B>A，但由DNL=3LSB=0.003V,模拟数据间的量化误差有0.003V，那么B-A会在-1(2-3=-1)到+5(2+3=5)之间的某一个数。

     

ADC的分辨率被定义为输入信号值的最小变化，这个最小数值变化会改变数字输出值的一个数值。对于一个理想ADC来说，传递函数是一个步宽等于分辨率的阶梯。然而，在具有较高分辨率的系统中（≥16位），传输函数的响应将相对于理想响应有一个较大的偏离。这是因为ADC以及驱动器电路导致的噪声会降低ADC的分辨率。

     A/D转换器的精确度是指对于给定模拟输入，实际数字输出与理论预期数字输出之间的接近度。换而言之，转换器的精确度决定了数字输出代码中有多少个比特表示有关输入信号的有用信息。

   

 

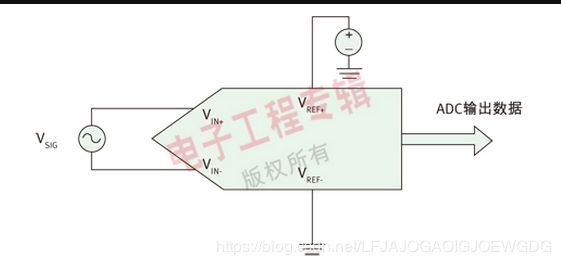
上图是基本ADC的测量电路，理想ADC生成一个数字输出代码，是关于模拟信号电压和电压参考输入的方程，其中输出代码 ＝满量程压 × [VIN+ - VIN-] / [VREF+ - VREF-]  ＝ 满量程电压 × [VIN /VREF]   
    每个数字输出代码表示参考电压的一个小数值。必须注意，ADC动态范围将要转换的信号的最大振幅，这样才能使ADC转换精度最大化。

    

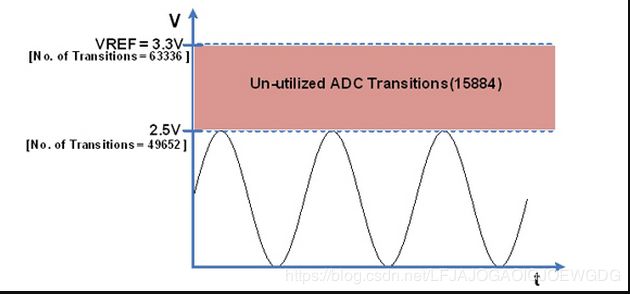
    如上图所示 ，假设Vin = 2.5V，Vref = 3.3V，那么对于16位ADC，最低有效位就为 3.3/2^16 = 50.35uV，如果ADC的最大信号为2.5V，那么 2.5 / 1LSB = 49652,结果有15884未被利用，这次转换后的精度或ENOB损失就为0.4位。ENOB(有效位数) ＝1.44ln(满量程/LSB) ，损失 = 总的位数 - ENOB；