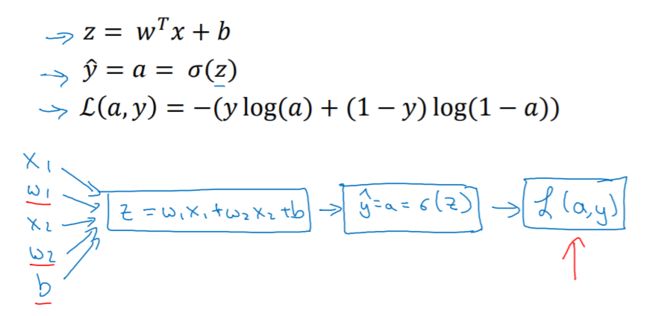吴恩达神经网络和深度学习——第二周笔记
Week2
目录
Week2
2-1二分分类
2.2logistic regression
2.3logistic回归的成本函数
2.4梯度下降
2.5、2.6均是高等数学中求导数的方法
2.7、2.8计算图及其导数计算
2.9logistic回归的梯度下降法
2-11
2-12
2-1二分分类
计算机如何保存一张图片?
计算机要保存一张图片,实质上是要保存三个矩阵,这三个矩阵分别对应RGB(red,green,blue)三个颜色的通道。例如输入的图片是64×64像素的,那么每一个矩阵的的大小就是64×64的,所以计算机就保存了3个64×64的矩阵,把这3个矩阵弄到一个向量X里,那么这个向量的维度就是64×64×3=12288=nx.
1.在二分类问题中,目标是训练出一个分类器。举个二分类的栗子,输入一张猫的图片,输出的就只有0,1,0表示这张图片不是猫,1表示这张图片是猫。这个分类器的输入就是上文的图片,也就是特征向量X,而输出是y,这个y的取值只有0或1。
一些符号规定
(x,y)表示一个单独的样本
x是xn维的特征向量
标签y值为0或1
训练集由m个训练样本构成,m个训练样本就是m张图片的意思
(x^(1), y^(1))表示样本1的输入和输出,
{x^(1), y(1),.....x(n), y^(n).}整个训练集2.2logistic regression
如何使用逻辑回归解决二分类问题?
逻辑回归中,我们希望预测值y的取值在0~1之间,这是与二分类模型不一样的地方。我们使用线性模型,引入参数w,b,得到
但是这样的值不是0~1的,所以我们再引入sigmoid函数
对这个函数进行分析:
如果z特别大,那么函数值就趋近0;如果z特别小,那么函数值就趋近于1.
2.3logistic回归的成本函数
Loss function定义为:
cost function定义为:
其中,loss function是对单个训练样本而言的,而cost function是对整个训练样本的loss function的平均值。也就是说成本函数cost function,它衡量的是在全体训练样本上的表现。
2.4梯度下降
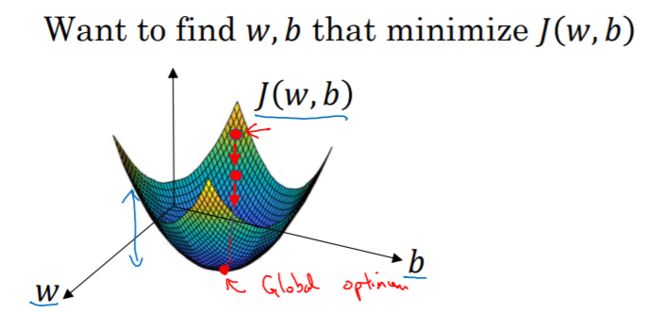
我们采用梯度下降法来训练或学习训练集上的参数w和b。我们要找到一个最合适的w,b使得成本函数最小。
可以看出,成本函数是一个凸函数,存在着一个全局最优解。
梯度下降法所做的就是,从初始点开始,朝最抖的下坡方向走一步,在梯度下降一步后,也许就会停在“碗”的最低端,因为它试着沿着最快下降的方向往下走,这是梯度下降的一次迭代。两次迭代可能就到了最低点,或者需要更多次,我们希望收敛到这个全局最优解,或接近全局最优解。
α是学习率,表示梯度下降的步长,即向下走一步的长度。
2.5、2.6均是高等数学中求导数的方法
2.7、2.8计算图及其导数计算
整个神经网络的训练过程分为两步:前向传播和反向传播。前向传播是从输入到输出,由神经网络计算,预测得到输出的过程。反向传播是从输出到输入,在计算梯度或导数。
前向传播
反向传播
2.9logistic回归的梯度下降法
因此我们在logistc回归中,需要做的就是变换参数w和b的值来最小化损失函数
2-11
向量化---消除代码中的for循环
c=np.dot(a,b)————两个矩阵相乘
2-12
u=np.zeros((n,1)) 意思是创建一个n维数组,且一行只有一个元素
如果已知一个向量u=np.zeros((10,1)),则他长这样子:
a = np.random.randn(5,1) #定义一个5行1列,,,就是列向量
print a
array([[ 0.96628706],
[-1.48066186],
[-0.55044832],
[-0.16443292],
[ 0.58546807]])
a = np.random.randn(1,5) #定义一个1行5列,,,就是行向量
print a
array([[ 1.01328334, -0.26443482, 1.1383514 , -1.09464648, 0.37793568]])