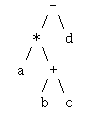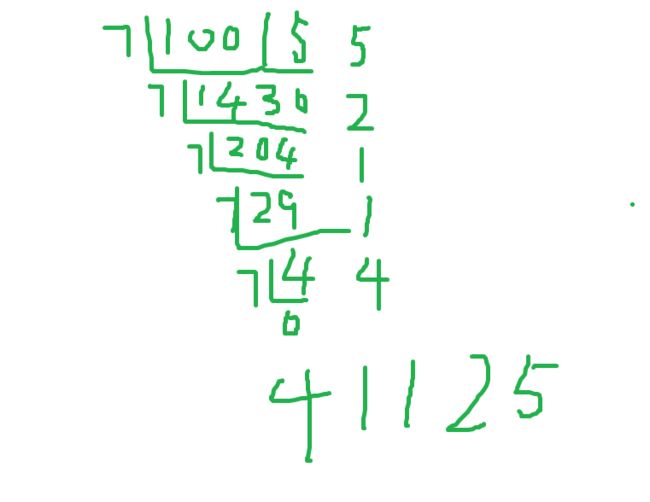2009年NOIP提高组初赛讲解(配图)

2009NOIP提高组初赛讲解 + 辅助图片

– by L_Y_T

看完觉得不错要留赞哦!

---

我的题库:https://blog.csdn.net/L_Y_T020321/article/details/83152606

要题面点这里
如果想要极差的体验也可以点这里
要答案点这里
T1:

A.世界上最早的计算机是1946年美国的ENIAC

B&C&D.1936年,图灵提出了一种新的计算模型—图灵机

---

T2
BIOS <==> “Basic Input Output System” ,基本输入输出系统

---

T3

---

T4

首先,开头是1,AC就排除了…,1111111111101101的反码是1111111111101100,原码是1000000000010011,然后就是$-19$

---

T5
5.m层满k叉树有$\frac{1-k^m}{1-k}$个节点,非叶节点有$k^m-1$个,叶节点有$k^{m-1}个,k^{m-1}=k^{m-1}=\frac{1-k^{m-1}}{1-k}\ast (k-1)+1$

---

T6
补棵树

---

T7
Huffman编码不允许一个编码是另一个的前缀

---

T8

图片选自洛谷大佬重启人的博客

T9
prim算法是指从起点开始,每次找与当前节点距离最短的节点进行扩展,已经被扩展的节点不在扩展
L_Y_T认为prim算法和dij是差不多的

---

T10
推荐链接:
chrome://dino//
来点点看

---

T11
摘自<信息学奥赛一本通(初赛篇)>P12页
“1972年,英特尔推出了世界上第一款微处理器4004”

位数只能说明处理的字长,所在系统的硬件指令不同,速度是很难说谁快谁慢的

---

T12
A项RAM不是随机位置储存,而是随时访问

是对一个字节的单元串行操作

内存应该是RAM,ROM和cache

1MB = 1024KB = 1024B * 1024 B

---

T13
多任务系统是单个CPU构架的,普通的PC都是多任务的.
操作系统不是都开源的QAQ

---

T14

A项的用很多层并不是为了兼容,而是根据网络分层模型来的

IPv6的标准是IPv4的升级与补充

必须要有IP地址才可以上网QAQ

---

T15
HTML并木有实现统一编码.本网站页面见也可以用超链接(而不是只能是书签)

---

T17
手动模拟一下
其实做这09年套题我就怪懵逼…
现在上网上搜索题解,结果…

为毛全是我的啊!!!(有的我还不会啊)

就像这道题.QAQ

因为这个玩意儿模拟的是循环队列(也就是队尾clist->next指向队首),在看题操作只有关于头部和尾部的…那就好说了
首先,A项是对的…来画个图图…

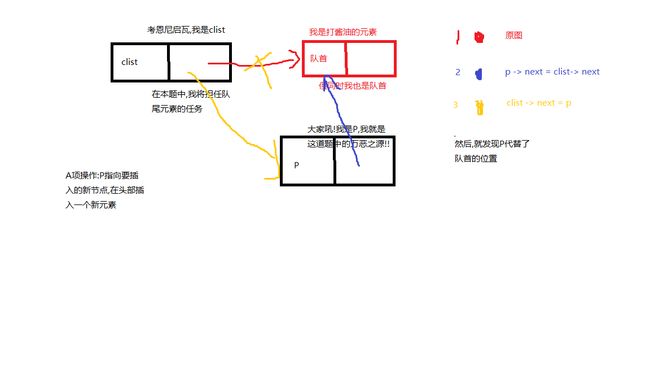
我才不会现场画图呢!
然后B图我就不画了哈!(有意见的~吱一声)
C项

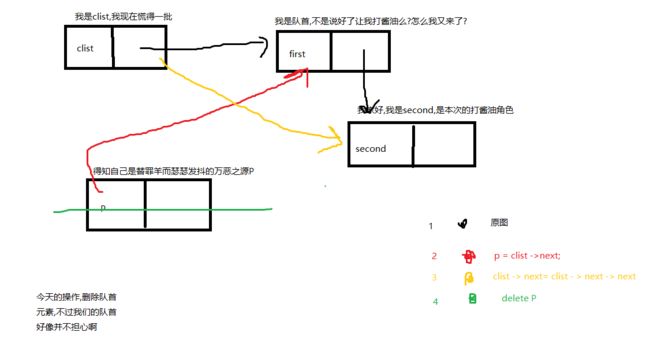
D项很明显的错了,不管了
(我才不会告诉你我不想画图了)

---

T18
不会!
好吧但是我可以按照窝自己的理解来试试(反正结果对了)

首先,我们把散列函数打出来H(K) = K % 11

然后,我们的数列先给打出来 $26,25,72,38,8,18,59$

散列出来后就是这样滴:____$4,3,6,5,8,7,4$

然后我们需要知道59存放的地址

然后,据观察,59的散列值为4

然后,稍微画出来是这样子

我们会发现,59就算是第一个那么最少也会在4这个格子上
按照散列值拍一下序,
$25_3,26_4,59_4,38_5,72_6,18_7,8_8$
所以,散列值在4之前的25可以说是没用了…

解析贼皮!

---

T19
见上面的一张图

---

T20
D项是什么!!??

---

填空题

---

1一定是序列中的第一个数字,接下来是2或者5,因为5后面没有后续的数字,因此我们先考虑2,然后

是3,然后是4和7,6要在4和7之后,根据乘法原理,1,2,3,4,6,7只有2种拍法,分别是1,2,3,4,7,6和

1,2,3,7,4,6,吧5插在1后面,共有6个位置,因此第一个联通快有2*6=12种拍法,再将8,9插进去,共有

1+2+3+…+8=36种方法,因此最后答案是12*36=432种.

摘自<信息学奥赛一本通(初赛篇)>

---

2
我萌吧$(10015{)}_{10}$化成7进制,然后进行计算

10进制转7进制不用多bb吧?

~~ 为了凑字数 ~~ 我还是说一下吧

丑死了…早知道不放了

然后进行计算,41125分别代表$4\ast 7^4,1\ast 7^3,1\ast 7^2,2\ast 7^1,5\ast 7^0$

然后,共需要4*7+1=29张$7^3$的,1张$7^2$的,2张$7^1$的,以及5张$7^0$的.共37张.

???

然后我们观察,5张一块的可以变成1张7快的然后找回2张一块

就成了37-5+3=35张.

---

程序阅读

---

1.第一题的work(b,a%b)暴露了一切/xyx但我就是要打出来!!

(QQ聊天的恶习)

不说了不说了在说就zz了(好像不说我也是啊)

#include 
#include 
#include 
#include 
using namespace std ;

int a , b ;
int work (int a , int b) {
	if(a % b) 
		return work(0,a%b) ;
	return b ;
}
int main() {
	cin >> a >> b ;
	cout << work(a,b) << "\n" ; 
	return 0 ;
} 

---

2.第二题模拟吧!?

我来试试手动模拟…(我先来存个当先)

好了,存完了
我来试试模拟
emmmm好怕啊

b[0], b[1],b[2],b[3]
a[0],a[1],a[2],a[3]

i = 0 ,
j = 0 ,a[0] = 2 , b[2] = 7

i = 1 ,
j = 0 , a[1] = 2 , a[0] = 2 ,b[2] = 9
j = 1 , a[1] = 5 , b[1] = 8

i = 2
j = 0 , a[2] = 2 , a[0] = 2 ,b[2] = 11
j = 1 , a[2] = 10 , a[1] = 5 , b[2] = 16
j = 2 , a[2] = 26 , b[2] = 42

i = 3
i = 0 , a[3] = 2 , a[0] = 2 , b[2] = 44
i = 1 , a[3] = 10 , a[1] = 5 , b[2] = 49
i = 2 , a[3] = 59 , a[2] = 26 , b[3] = 33
i = 3 , a[3] = 92 , b[0] = 94

辛苦打一张表
其实也可以…

#include 
#include 
using namespace std ;
int main() {
	int a[4] , b[4] ;
	int i , j , tmp ;
	for(i = 0 ; i < 4 ; i ++ )
	cin >>b[i] ;
	for(int i = 0 ; i < 4 ; i ++) {
		a[i] = 0 ;
		for(int j = 0 ; j <= i ; j ++) {
			a[i] += b[j] ;
			b[a[i]%4] += a[j] ;
		}
	} 
	tmp = 1 ;
	for(int i = 0 ; i < 4 ; i ++) {
		a[i] %= 10 ;
		b[i] %= 10 ;
		tmp *= a[i] + b[i] ; 
	}
	cout << tmp << endl ;
	return 0 ;
}

这样好像更方便的样子(码风怪丑,不要介意)…

---

这个…
看code中的这两句话…
c[i][0] = 1
c[i][i] = 1
然后打出表来

1
1 1
1   1
1     1
1      1
1        1
1          1
1             1

就是这个样子
然后又有… f[i][j] = f[i - 1][j - 1] + f[i - 1][j]

好了,很明显了,我们可爱的杨辉三角!!

那么题目就是求杨辉三角第n行的和了
链接

然后第n行的系数和就是$2^n$

#include 
#include 
#include 
#include 
#define maxn 50
const int y = 2009 
using namespace std ;
int n , c[maxn][maxn] , i , j , s = 0 ; 
int main() {
	cin >> n ;
	c[0][0] = 1 ;
	for(int i = 1 ; i <= n ; i ++) {
		c[i][0] = 1 ;
		for(int j = 1 ; j <= n ; j ++) {
			c[i][j] = c[i-1][j] + c[i-1][j-1] ;
		}
		c[i][i] = 1 ;
	}
	for(int i = 0 ; i <= n ; i ++)
		s = (s+c[n][i]) % y ;
	cout << s << "\n" ;  
	return 0 ;
}

---

3.本题是将两数相除边小数

#include 
#include 
#include 
#include 

int n , m , i , j , p , k ;
int a[100] , b[100] ;
int main() {
	cin >> n >> m ;
	a[0] = n ; i = 0 ; p = 0 ; k = 0 ;
	do{
		for(int j = 0 ; j < i ; j ++) 
			if(a[i] == a[j]) {
				p = 1 ;
				k = j ;
				break ;
			}
		if(p) break ;
		b[i] = a[i]/m ;
		a[i+1] = a[i] % m * 10 ;
		i ++ ;
	}while(a[i] != 0) ;
	cout << b[0] <<"." ;
	for(j = 1 ; j < k ; j ++ ) cout << b[j] ;
	if(p) cout << "(" ;
	for(j = k ; j < i ; j ++ ) cout << b[j] ;
	if(p) cout << ")" ;
	cout << endl ;
	return 0;
}

---

完形填空
答案如下:

(1)0
(2)tmp + a[i] == ans
(3) < 0
(4)i
(5)tmp += a[i]

解析:
首先来解释一下变量:ans就是所求的和,len就是长度,beg就是起始位置的前一个位置,而i - beg正好

就是当前所选的序列的长度,tmp是当前序列的和,知道了beg的含义后,$1$就应该是起始位置1的

前一个,所以$1$填0.然后就开始逐一扫描,因为是连续和,所以一重循环即可首先判断这个数是否

使解更优,更优就填进去,否则就看是否与最优解相等,相等的话就按照题目,选取长度更长的,在进行

长度判断,因此$2$就填tmp + a[i] == ans . 如果当前解释负数,如果下一个数是>0的,那么就要舍弃

所有的数选下一个数,如果下一个数是负的,那么加上之后肯定更小,所以不管下一个数正负,当前解

都要舍掉,所以重新清零,因此$3$填 < 0 ,tmp 归零 .,beg是起始位置的前一个数,而起始位置是下一

个数,所以让beg = i , 即$4$填i .如果当前解> 0 ,那就保留, 即$5$ tmp += a[i]

---

(1)now <= maxnum
(2)second - first
(3)(ans-1)
(4)hash[first] >= ans
(5)ok
(6)work(0)

解析:题目要求最大的L,因此采取穷举的方法.从N开始,引入一个work函数判断是否可以使全部的

数分为长度均为ans的等差数列,所以我们想的的ans必须是n的约数,且使这些数可以满足条

件,hash是用来记录每个数字出现的次数的,maxnum为这些数中最大的一个,now就是一个等差数

列开始的数,由于数是0~59 , 所以可能的最小的值为0,因此$6$填work(0),但并不是0~59所有的数

都出现,所以hash里有的值为0,所以扫描的时候要跳过这些数,因此work一开始就跳过这写数,判断

是$hash[now]=0$ , 还有一个就是$now<=maxnum$,因为maxnum是最大的,但不一定是59,所

以$1$填$now<=maxnum$ ,找到了一个等差数列的起始项,那么第二项是啥呢?不能确定,因此枚

举第二项,delta就是公差,因此填$second-first$,长度为 ans 的等差数列起始项为first,公差是delta,

末项是$first+(ans-1)\ast delta$,如果末项比maxnum大,那么肯定不合法,而下一个second肯定比现在

的大,那就意味着公差和末项都要变大,那是不可能的,所以只能让ans变小,所以$3$填(ans-1).ok是

用来检验等差数列是否存在的,如果delta == 0 ,那就意味着至少要有ans个first才合法,因此$4$填

hash[now] >= ans .如果delta 不为 0 , 那就逐一检查,hash[first+delta*i] == 0则OK就应该改为false,

如果感觉不错就给个赞哟!