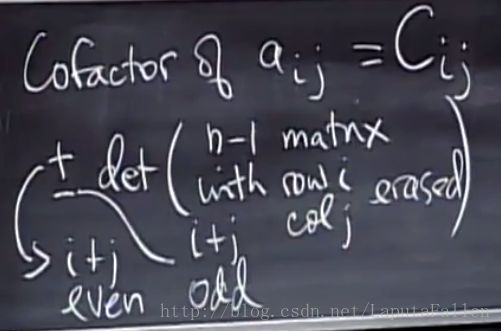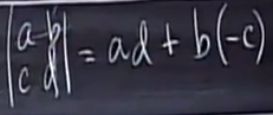MIT线性代数笔记-第十九讲

Formula for detA

先看一下determinant最核心的三个性质:
1. detI=1 d e t I = 1
2.sign reverse with row exchange
3.det is linear in each row separately
现在我们要用这三个性质来推出detA的一般公式

先看一下2*2的例子:
∣∣∣acbd∣∣∣=∣∣∣ac0d∣∣∣+∣∣∣0cbd∣∣∣=∣∣∣ac00∣∣∣+∣∣∣a00d∣∣∣+∣∣∣0cb0∣∣∣+∣∣∣00bd∣∣∣=∣∣∣a00d∣∣∣+∣∣∣0cb0∣∣∣=ad−cb | a b c d | = | a 0 c d | + | 0 b c d | = | a 0 c 0 | + | a 0 0 d | + | 0 b c 0 | + | 0 b 0 d | = | a 0 0 d | + | 0 b c 0 | = a d − c b
由这个简单的例子我们可以推广到n*n
我们想象一下，如果是3*3，我们会分解出3*3*3 = 27个矩阵，但是里面很多矩阵的det都为0，那么哪些不为0，答案是排列，即为3！ = 6个。
看一下3*3的例子

∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣=∣∣∣∣a11000a22000a33∣∣∣∣+∣∣∣∣a110000a320a230∣∣∣∣+∣∣∣∣0a210a120000a33∣∣∣∣+∣∣∣∣00a31a12000a230∣∣∣∣+∣∣∣∣0a21000a32a1300∣∣∣∣+∣∣∣∣00a310a220a1300∣∣∣∣= | a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 | = | a 11 0 0 0 a 22 0 0 0 a 33 | + | a 11 0 0 0 0 a 23 0 a 32 0 | + | 0 a 12 0 a 21 0 0 0 0 a 33 | + | 0 a 12 0 0 0 a 23 a 31 0 0 | + | 0 0 a 13 a 21 0 0 0 a 32 0 | + | 0 0 a 13 0 a 22 0 a 31 0 0 | =
a11a22a33−a11a32a23−a21a12a33+a31a12a23+a21a32a13−a31a22a13 a 11 a 22 a 33 − a 11 a 32 a 23 − a 21 a 12 a 33 + a 31 a 12 a 23 + a 21 a 32 a 13 − a 31 a 22 a 13

OK，我们来看看n * n 的一般公式:

看一个例子:

通过big formula,我们很容易就得出这个矩阵的det为0，为奇异矩阵

Cofactor formula

我们回到这个例子
∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣=∣∣∣∣a11000a22000a33∣∣∣∣+∣∣∣∣a110000a320a230∣∣∣∣+∣∣∣∣0a210a120000a33∣∣∣∣+∣∣∣∣00a31a12000a230∣∣∣∣+∣∣∣∣0a21000a32a1300∣∣∣∣+∣∣∣∣00a310a220a1300∣∣∣∣= | a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 | = | a 11 0 0 0 a 22 0 0 0 a 33 | + | a 11 0 0 0 0 a 23 0 a 32 0 | + | 0 a 12 0 a 21 0 0 0 0 a 33 | + | 0 a 12 0 0 0 a 23 a 31 0 0 | + | 0 0 a 13 a 21 0 0 0 a 32 0 | + | 0 0 a 13 0 a 22 0 a 31 0 0 | =
a11a22a33−a11a32a23−a21a12a33+a31a12a23+a21a32a13−a31a22a13 a 11 a 22 a 33 − a 11 a 32 a 23 − a 21 a 12 a 33 + a 31 a 12 a 23 + a 21 a 32 a 13 − a 31 a 22 a 13
这个矩阵的det用cofactors表示如下:
a11(a22a33−a23a32)+a12()+a13() a 11 ( a 22 a 33 − a 23 a 32 ) + a 12 ( ) + a 13 ( )
我们需要把注意力集中在括号里的式子，来看看选择 a11 a 11 的情况:

a11对应的cofactor即剩下的2(n - 1)行2(n - 1)列的det(还要添加上符号，根据选择元素的i和j之和为奇数还是偶数确定，若为偶数，则为正号，若为奇数，则为负号)

cofactor的定义如下:

来看一个2*2的例子:

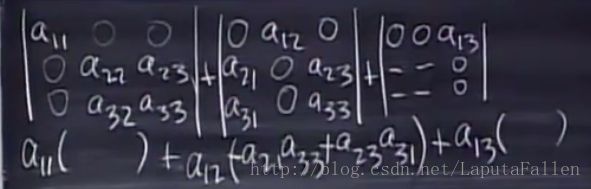
Tridiagonal matrices

得出三对角线矩阵det的规律后，我们可以继续求得| A5 A 5 | = 0,| A6 A 6 | = 1,| A7 A 7 | = 1,它的det是以6为循环的奇妙的组合。