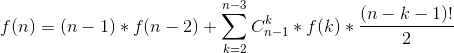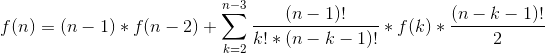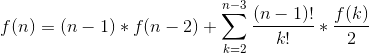牛客多校第一场 B Symmetric Matrix(组合数公式+dp)
链接:https://www.nowcoder.com/acm/contest/139/B
来源:牛客网
题目描述
Count the number of n x n matrices A satisfying the following condition modulo m.
* Ai, j ∈ {0, 1, 2} for all 1 ≤ i, j ≤ n.
* Ai, j = Aj, i for all 1 ≤ i, j ≤ n.
* Ai, 1 + Ai, 2 + ... + Ai, n = 2 for all 1 ≤ i ≤ n.
* A1, 1 = A2, 2 = ... = An, n = 0.
输入描述:
The input consists of several test cases and is terminated by end-of-file. Each test case contains two integers n and m.
输出描述:
For each test case, print an integer which denotes the result.
示例1
输入
复制
3 1000000000 100000 1000000000
输出
复制
1 507109376
备注:
* 1 ≤ n ≤ 105 * 1 ≤ m ≤ 109 * The sum of n does not exceed 107.
题目大意:给出n和m,要你构造出满足如下条件的n*n的矩阵,
1、矩阵内的元素A[i][j] = {0,1,2}
2、矩阵内的元素A[i][j] = A[j][i]
3、矩阵内的元素A[i][1]+A[i][2]+A[i][3]+...+A[i][n]=2 对于所有的 i 都成立
4、矩阵内的元素A[i][i]=0 对于所有的 i 都成立
问你有多少中构造方案
题目思路:可以把这个矩阵看做是无向图的邻接矩阵,那么我们就可以把问题转化为求无向图中所有点的度数都为2的图有多少个。我们考虑f[n]表示n个结点的图满足条件的数量。
接下来我们考虑图中的最后一个点所在的环中有多少个结点,当最后一个环只有两个结点的时候
![]()
表示从除最后一个点以外的n-1个点中选出1个点与最后一个点形成环,前n-2个点形成满足条件的图的总情况有多少,
再考虑最后一个点所在的环有n-k(k>=2)个结点的情况
我们可以先从前n-1个结点中选出k个结点形成满足条件的图,那么剩下的n-k-1个结点就有(n-k-1)!种形成链的方式(因为每个点的度为2,且这n-k-1个结点要与最后一个点形成环,所以这n-k-1个结点只会形成链),然后我们再加入最后一个结点与这条链的首尾相连形成环,由于首尾的顺序与形成的环的方式是无关的,所以这里要除以一个2将重复的情况去除(比如1,2,3三个结点的全排列中就有1,2,3和3,2,1两种,由于它是无向图,所以在加入最后一个结点4之后形成的环都是1-2-3-4-1,就有一种情况重复计算了)。
最后推出来的式子为
综上所述可得如下式子
通过上述式可得
![]()
![]()
递推式就推完毕了,具体实现看代码:
#include
#define fi first
#define se second
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define pb push_back
#define MP make_pair
#define FIN freopen("in.txt","r",stdin)
#define fuck(x) cout<<"["<pii;
const int MX=1e5+7;
int n,m;
ll f[MX];
int main(){
while(~scanf("%d%d",&n,&m)){
if(m==1){
printf("0\n");
continue;
}
f[1]=0;
f[2]=f[3]=1;
for(int i=4;i<=n;i++){
f[i]=((i-1)*(f[i-1]+f[i-2])%m-(ll)(i-1)*(i-2)/2*f[i-3]+m)%m;
}
printf("%lld\n",(f[n]+m)%m);
}
return 0;
}