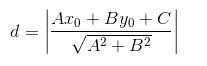一种快速在向量空间中寻找k紧邻的算法——annoy index

几个需要关注的点：

1.这是一个精确度换速度的算法，找到的k紧邻不能保证是全局的k紧邻（例如在分割平面附近的点），所以如果要找exact的k紧邻的话并不合适，还是得做全局的搜索

2.可以通过设置tree的数量来balance精度和速度

3.每次对同一份数据建立索引是不同的，所以两次计算结果可能也会不同

4.github：https://github.com/spotify/annoy

最近工作中使用了一下annoy，于是抽时间看了下代码，记录下。。

annoy支持三种距离度量方式，cos距离，欧式距离和曼哈顿距离。下面主要通过最简单的欧氏距离来看。

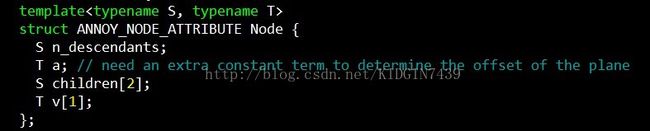
首先看下节点node的结构

n_descendants记录了该节点下子节点的个数，children[2]记录了左右子树，v和a之后会详细说，先知道v[1]代表该节点对应的向量，a代表偏移就好。

然后看下AnnoyIndex类

_n_items记录了我们一共有多少个向量需要构建索引，_n_nodes记录了一共有多少个节点，_s是node占有的空间大小，_f是向量的维度，_nodes所有节点，_roots是所有树的根节点。

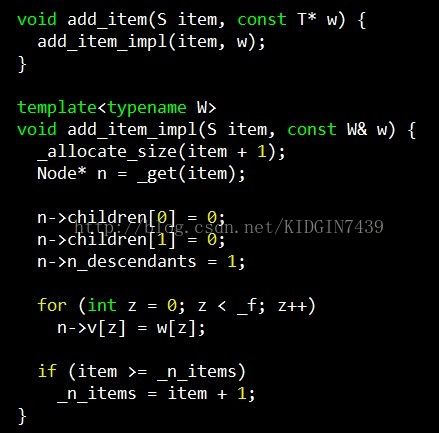
annoy建树的时候当该区域内的节点数小于k的时候就不会再继续递归建树，之前疑惑怎么调整k这个参数，看完代码才发现没法调整，_K是一个定值，如果一个区域内的节点数小于_K的时候，这个节点就不再记录向量v，v的空间也用来记录节点的id。

另外还有一个比较奇怪的事情就是annoy为node开辟空间的方式。。比如我有三个item，建索引的时候id分别为3,6,10，那么annoy会开辟11个node空间，从0-10。。看下面这段代码就能明白

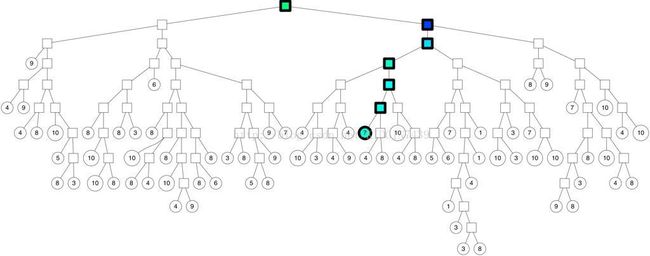
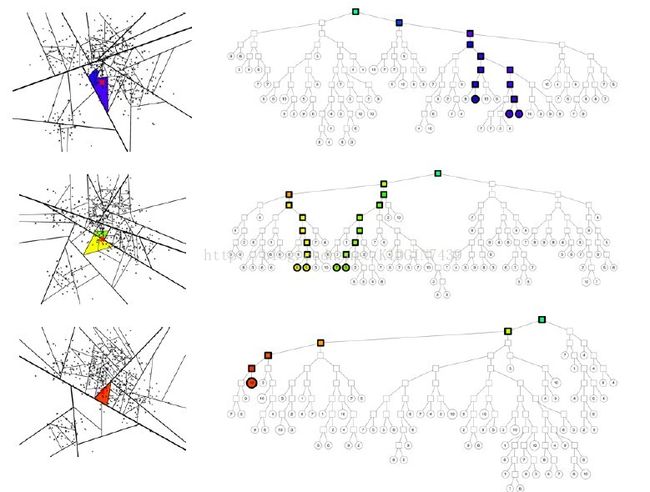
再接下来就是到了建树。annoy建树如下图，每次选择空间中的两个质心作为分割点，相当于kmeans过程，以使得两棵子树分割的尽量均匀以保证logn的检索复杂度。以垂直于过两点的直线的超平面来分割整个空间，然后在两个子空间内递归分割直到子空间最多只有k个点。如下图

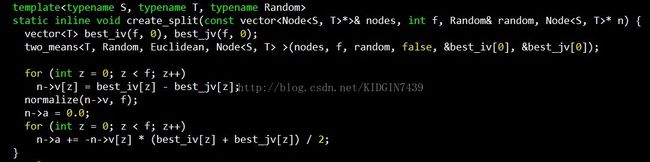
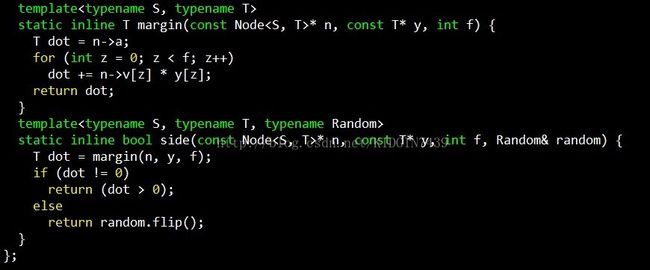
然后看下创建分割面的过程，入参为当前空间的所有点nodes，维度f，随机函数random，分割节点n

best_iv和best_jv就是选出来的那两个点，n->v存储的就是这两个点连线对应的向量，即分隔面的法向量，计算方式就是两点对应向量相减。n->a存储的就是分割超平面对应的偏移，以三维空间举例，三维空间中的平面表示方法为Ax + By + Cz + D = 0，n->a存储的就是这个D，计算方法如下，因为平面的法向量已经确定，又因为该平面过best_iv和best_jv连线中点，将中点坐标代入，连线中心点定义为m=((best_iv[0] + best_jv[0])/2, (best_iv[1] + best_jv[1])/2, (best_iv[2] +best_jv[2])/2)，则A * m[0] + B * m[1] + C * m[2] + D =0  => D= -(A * m[0] +B * m[1] + C * m[2])。

接下来看一下是如何选择两个点的，即two_means

为了保证nlogn的检索复杂度，需要使得每次分割得到的两棵子树尽量平衡，所以要找空间中的两个质心，过程很像kmeans，初始随机选取两个点，每次迭代过程中随机选择一个点计算该点属于哪个子树，并更新对应的质心坐标。

建树完成之后就是检索，对于给定的点去树中找topk近邻，最基本的想法就是从根开始，根据该点的向量信息和每个树节点的分割超平面比较决定去哪个子树遍历。如图所示

但是这样还是存在一些问题，就是最近邻不一定会和查询点在同一个叶结点上

解决方法是这样的，一是建立多棵树，二是在查询点遍历树的时候不一定只选择一条路径，这两个方法对应两个参数treenum和searchnum，如图所示

遍历过程中用优先队列维护候选集合，将所有树的结果去重维护到优先队列中，最后对这些候选集合计算距离并返回topk

 

首先看两个小函数，这是在树上遍历的时候计算点到超平面的距离并确定在哪棵子树的函数，点到平面的距离函数为

因为每个树节点中的超平面向量已经被归一化到1了，所以只需计算分子即可。

然后看下检索函数，

nns是候选集合，search_k即前面提到的search_num

首先是将所有树的根节点压入优先队列中，每次取出优先队列的头结点进行遍历，如果头结点为叶结点，则将该树节点对应的所有点加入到nns中，如果是非叶结点，则将两棵子树都加入到优先队列中，以此循环遍历直到nns中节点超过searchnum，最后对nns中的id去重后计算距离返回。

最后说下遇到的另一个问题，我们度量距离的方式为向量内积，内积并不能使用lsh方法来计算最近邻，为了解决这个问题，我们将内积距离转换为了cos距离，具体做法为在建立索引时，将所有向量的每一维除以c，c设置为所有向量中最大的模长，并将所有向量增加一维，设置为1减去其他维的平方的和再开根。这样就可以把cos距离中的分母消去了索引向量模长，而检索向量的模长并不会影响排序。

参考：

http://blog.csdn.net/hero_fantao/article/details/70245387

annoy作者的ppt

Annoy

   

Annoy (Approximate Nearest Neighbors Oh Yeah) is a C++ library with Python bindings to search for points in space that are close to a given query point. It also creates large read-only file-based data structures that are mmapped into memory so that many processes may share the same data.

Install

To install, simply do sudo pip install annoy to pull down the latest version from PyPI.

For the C++ version, just clone the repo and #include "annoylib.h".

Background

There are some other libraries to do nearest neighbor search. Annoy is almost as fast as the fastest libraries, (see below), but there is actually another feature that really sets Annoy apart: it has the ability to use static files as indexes. In particular, this means you can share index across processes. Annoy also decouples creating indexes from loading them, so you can pass around indexes as files and map them into memory quickly. Another nice thing of Annoy is that it tries to minimize memory footprint so the indexes are quite small.

Why is this useful? If you want to find nearest neighbors and you have many CPU's, you only need the RAM to fit the index once. You can also pass around and distribute static files to use in production environment, in Hadoop jobs, etc. Any process will be able to load (mmap) the index into memory and will be able to do lookups immediately.

We use it at Spotify for music recommendations. After running matrix factorization algorithms, every user/item can be represented as a vector in f-dimensional space. This library helps us search for similar users/items. We have many millions of tracks in a high-dimensional space, so memory usage is a prime concern.

Annoy was built by Erik Bernhardsson in a couple of afternoons during Hack Week.

Summary of features

• Euclidean distance, Manhattan distance, cosine distance, or Hamming distance
• Cosine distance is equivalent to Euclidean distance of normalized vectors = sqrt(2-2*cos(u, v))
• Works better if you don't have too many dimensions (like <100) but seems to perform surprisingly well even up to 1,000 dimensions
• Small memory usage
• Lets you share memory between multiple processes
• Index creation is separate from lookup (in particular you can not add more items once the tree has been created)
• Native Python support, tested with 2.6, 2.7, 3.3, 3.4, 3.5

Python code example

from annoy import AnnoyIndex
import random

f = 40
t = AnnoyIndex(f)  # Length of item vector that will be indexed
for i in xrange(1000):
    v = [random.gauss(0, 1) for z in xrange(f)]
    t.add_item(i, v)

t.build(10) # 10 trees
t.save('test.ann')

# ...

u = AnnoyIndex(f)
u.load('test.ann') # super fast, will just mmap the file
print(u.get_nns_by_item(0, 1000)) # will find the 1000 nearest neighbors

Right now it only accepts integers as identifiers for items. Note that it will allocate memory for max(id)+1 items because it assumes your items are numbered 0 … n-1. If you need other id's, you will have to keep track of a map yourself.

Full Python API

• AnnoyIndex(f, metric='angular') returns a new index that's read-write and stores vector of f dimensions. Metric can be "angular", "euclidean", "manhattan", or "hamming".
• a.add_item(i, v) adds item i (any nonnegative integer) with vector v. Note that it will allocate memory for max(i)+1 items.
• a.build(n_trees) builds a forest of n_trees trees. More trees gives higher precision when querying. After calling build, no more items can be added.
• a.save(fn) saves the index to disk.
• a.load(fn) loads (mmaps) an index from disk.
• a.unload() unloads.
• a.get_nns_by_item(i, n, search_k=-1, include_distances=False) returns the n closest items. During the query it will inspect up to search_k nodes which defaults to n_trees * n if not provided. search_k gives you a run-time tradeoff between better accuracy and speed. If you set include_distances to True, it will return a 2 element tuple with two lists in it: the second one containing all corresponding distances.
• a.get_nns_by_vector(v, n, search_k=-1, include_distances=False) same but query by vector v.
• a.get_item_vector(i) returns the vector for item i that was previously added.
• a.get_distance(i, j) returns the distance between items i and j. NOTE: this used to return the squared distance, but has been changed as of Aug 2016.
• a.get_n_items() returns the number of items in the index.

Notes:

• There's no bounds checking performed on the values so be careful.
• Annoy uses Euclidean distance of normalized vectors for its angular distance, which for two vectors u,v is equal to sqrt(2(1-cos(u,v)))

The C++ API is very similar: just #include "annoylib.h" to get access to it.

Tradeoffs

There are just two parameters you can use to tune Annoy: the number of trees n_trees and the number of nodes to inspect during searching search_k.

• n_trees is provided during build time and affects the build time and the index size. A larger value will give more accurate results, but larger indexes.
• search_k is provided in runtime and affects the search performance. A larger value will give more accurate results, but will take longer time to return.

If search_k is not provided, it will default to n * n_trees where n is the number of approximate nearest neighbors. Otherwise, search_k and n_trees are roughly independent, i.e. a the value of n_trees will not affect search time if search_k is held constant and vice versa. Basically it's recommended to set n_trees as large as possible given the amount of memory you can afford, and it's recommended to set search_k as large as possible given the time constraints you have for the queries.

How does it work

Using random projections and by building up a tree. At every intermediate node in the tree, a random hyperplane is chosen, which divides the space into two subspaces. This hyperplane is chosen by sampling two points from the subset and taking the hyperplane equidistant from them.

We do this k times so that we get a forest of trees. k has to be tuned to your need, by looking at what tradeoff you have between precision and performance.

Hamming distance (contributed by Martin Aumüller) packs the data into 64-bit integers under the hood and uses built-in bit count primitives so it could be quite fast. All splits are axis-aligned.

More info

• Dirk Eddelbuettel provides an R version of Annoy.
• Andy Sloane provides a Java version of Annoy although currently limited to cosine and read-only.
• Pishen Tsai provides a Scala wrapper of Annoy which uses JNA to call the C++ library of Annoy.
• There is experimental support for Go provided by Taneli Leppä.
• Boris Nagaev wrote Lua bindings.
• During part of Spotify Hack Week 2016 (and a bit afterward), Jim Kang wrote Node bindings for Annoy.
• Min-Seok Kim built a Scala version of Annoy.
• Presentation from New York Machine Learning meetup about Annoy
• Radim Řehůřek's blog posts comparing Annoy to a couple of other similar Python libraries: Intro, Contestants, Querying
• ann-benchmarks is a benchmark for several approximate nearest neighbor libraries. Annoy seems to be fairly competitive, especially at higher precisions:

Source code

It's all written in C++ with a handful of ugly optimizations for performance and memory usage. You have been warned :)

The code should support Windows, thanks to Qiang Kou and Timothy Riley.

To run the tests, execute python setup.py nosetests. The test suite includes a big real world dataset that is downloaded from the internet, so it will take a few minutes to execute.

Discuss

Feel free to post any questions or comments to the annoy-user group. I'm @fulhack on Twitter.