常见的连续概率分布

高斯分布

高斯分布是统计学与机器学习中使用最广泛的分布，他的概率密度函数( pdf )：

N(x|μ,σ2)=12πσ2−−−−√e−(x−μ)22σ2

高斯分布的精度： λ=1/σ2 ，精度越高意味着高斯分布越集中在 μ 附近。

累计分布函数： Φ(x;μ,σ2)=∫x−∞N(z|μ,σ2)dz

$Φ(x;μ,σ2)=12[1+erf(z/2√)]

其中 z = (x-\mu)/\sigma ， erf(x)=\frac{2}{\sqrt{\pi}}\int_0^{x}e^{-t^{2}}dt$

退化分布

当 σ2→0 时，高斯分布就集中在 μ 上：
limσ2→0N(x|μ,σ2)=δ(x−u)
其中 δ 是 狄拉克 δ 函数

δ(x)={∞0 if x = 0  if otherwise

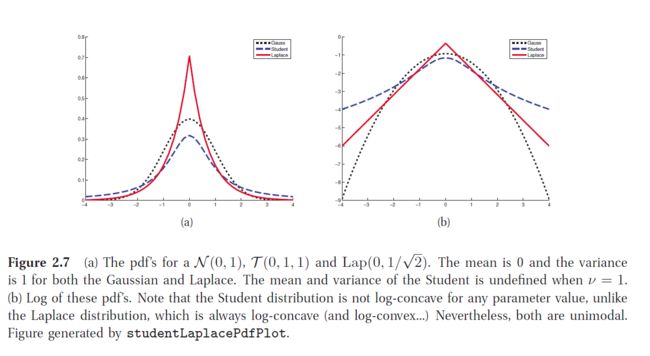
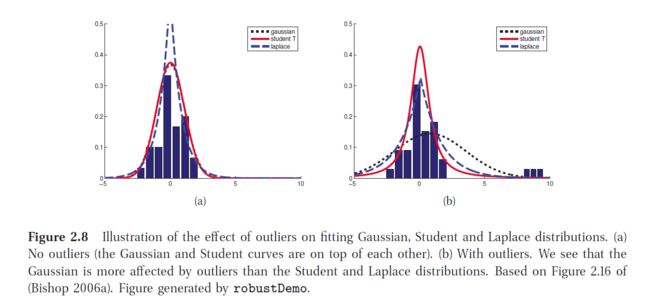
Student t 分布

T(x|μ,σ2,ν)∝[1+1ν(x−μσ)2]−(ν+12)

拉普拉斯分布

Lap(x|μ,b)=12bexp(−|x−μ|b)

其中 mean=μ,mode=μ,var=2b2 ，拉普拉斯分布对离散点比高斯分布更鲁棒。并且在很多点上的概率密度都为0，因此可以用来稀疏化一个模型。

伽马分布

伽马分布是一个对正实数随机变量很灵活的分布， Ga(T|shape=a,rate=b)=baΓ(a)Ta−1e−Tb ， a>0,b>0

其中， Γ(x)=∫∞0μx−1e−μdμ

并且 mean=ab,mode=a−1b,var=ab2

伽马的逆： IG(x|shape=a,scale=b)=baΓ(a)T−(a+1)e−b/x

如果 X∼Ga(a,b) ， 则 1X∼IG(a,b)

而且该分布： mean=ba−1,mode=ba+1,var=b2(a−1)2(a−2)

集中特殊情况下的伽马分布

1. 指数分布： Exp(x|λ)=Ga(x|1,λ)
2. Erlang分布： Erlang(x|λ)=Ga(x|2,λ)
3. Chi-squared分布： χ2(x|ν)=Ga(x|ν2,12) 。如果 Zi∼N(0,1),S=∑νi=1Z2i ，那么 S∼χ2ν

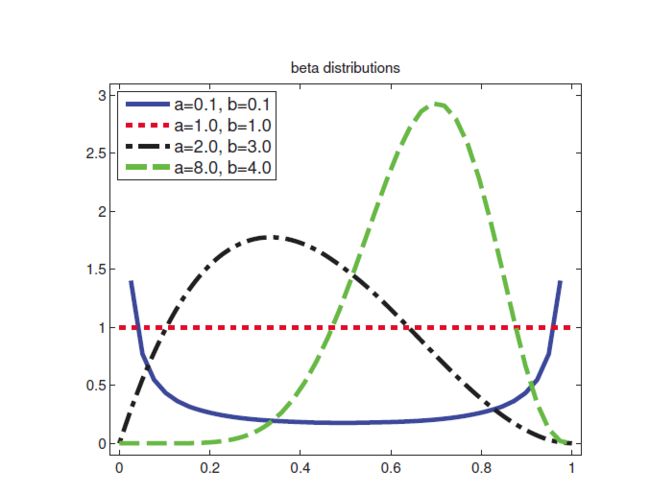
贝塔分布

贝塔分布在[0,1]内， Beta(x|a,b)=1B(a,b)xa−1(1−x)b−1 ，其中 B(a,b)=Γ(a)Γ(b)Γ(a+b)

mean=aa+b,mode=a−1a+b−2,var=ab(a+b)2(a+b+1)

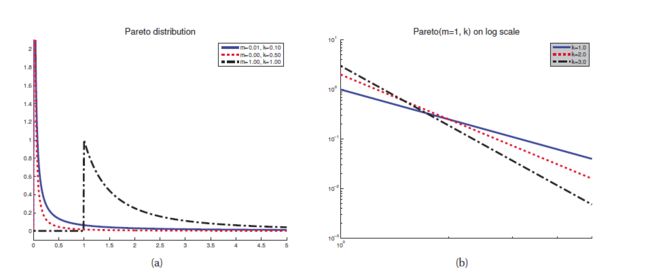
帕累托分布

80/20法则: Pareto(x|k,m)=kmkx−(k+1)1(x≥m)

mean=kmk−1,mode=m,var=m2k(k−1)2(k−2)

参考

Machine Learning A Probabilistic Perspective
帕累托分布