
package com.learn.btree;
/**
* 二叉链表的节点
* @author Leon.Sun
*
*/
public class Node {
/**
* 节点的值
*/
// private Object value;
Object value;
/**
* 左孩子
* 左子树的引用
* 同样为了处理方便,我们把private去掉
*/
// private Node leftChild;
Node leftChild;
/**
* 右子树的引用
*/
// private Node rightChild;
Node rightChild;
public Node() {
super();
}
public Node(Object value) {
super();
this.value = value;
}
public Node(Object value, Node leftChild, Node rightChild) {
super();
this.value = value;
this.leftChild = leftChild;
this.rightChild = rightChild;
}
/**
* 这个toString该怎么写呢
* 输出三个属性的值就可以了
*/
@Override
public String toString() {
return "Node [value=" + value + ", leftChild=" + leftChild + ", rightChild=" + rightChild + "]";
}
}
package com.learn.btree;
/**
* 二叉树接口
* 可以有不同的实现类,每个类可以使用不同的存储结构,比如顺序结构、链式结构
* 链式结构可以是二叉的,也可以是三叉的
* @author Leon.Sun
*
*/
public interface BinaryTree {
/**
* 是否空树
* 你的树是空的吗,空是什么意思
* 有没有根节点,有根就不是空的了
* @return
*/
public boolean isEmpty();
/**
* 树结点数量
* 树里面有几个节点
* @return
*/
public int size();
/**
* 获取二叉树的高度
* 得到树的高度
* @return
*/
public int getHeight();
/**
* 查询指定值的结点
* 在树里面去找一个值
* 我去找20,要告诉我这里没有20才可以
* @param value
* @return
*/
public Node findKey(int value); // 查找
/**
* 前序递归遍历
* 这三个遍历要采用递归来实现
*/
public void preOrderTraverse();
/**
* 中序遍历递归操作
*/
public void inOrderTraverse();
/**
* 后序遍历递归操作
*/
public void postOrderTraverse();
/**
* 后序遍历递归操作
* 这个是重载,一个有参,一个无参
* @param node 树根结点
*/
public void postOrderTraverse(Node node);
/**
* 中序遍历非递归操作
* 1)对于任意节点current,若该节点不为空则将该节点压栈,并将左子树节点置为current,重复此操作,直到current为空。
* 2)若左子树为空,栈顶节点出栈,访问节点后将该节点的右子树置为current
* 3) 重复1、2步操作,直到current为空且栈内节点为空。
*/
public void inOrderByStack();
/**
* 前序遍历非递归操作
* 1)对于任意节点current,若该节点不为空则访问该节点后再将节点压栈,并将左子树节点置为current,重复此操作,直到current为空。
* 2)若左子树为空,栈顶节点出栈,将该节点的右子树置为current
* 3) 重复1、2步操作,直到current为空且栈内节点为空。
*/
public void preOrderByStack();
/**
* 后序遍历非递归操作
* 1)对于任意节点current,若该节点不为空则访问该节点后再将节点压栈,并将左子树节点置为current,重复此操作,直到current为空。
* 2)若左子树为空,取栈顶节点的右子树,如果右子树为空或右子树刚访问过,则访问该节点,并将preNode置为该节点
* 3) 重复1、2步操作,直到current为空且栈内节点为空。
*/
public void postOrderByStack();
/**
* 按照层次遍历二叉树
* 这个需要借助队列来实现,这里还是包含很多技能点的
*/
public void levelOrderByStack();
}
package com.learn.btree;
import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;
/**
* 如果以后别人问你二叉树,二叉树进行层次遍历,应该怎么来实现
* 能用递归吗,不能用递归,怎么办,不能说借助while循环和for循环
* 就是借助队列,什么个原理啊,先把根放到队列里面去,
* 根出队,根出队之前,它会把根的两个孩子都放到队列里面去,
* 自左向右放,把第一层处理完之后,第二层的节点已经在队列里面了
* 然后再处理第二层的节点,在处理第二层的节点之后已经把第三层的节点从左至右依次加到队列里面去了
* 然后再处理第三层节点了,第三层节点处理之后就把第四层节点放到队列里面去
* 队列是先进先出,我们是先放左边的再放右边的,所以先遍历左边的,再遍历右边的
* 这里面什么时候结束了,队列是空,队列是空所有的节点都遍历完了
* 它是按照这个思路来的,这是我们按层次遍历的
* 代码好好的理解一下,大循环里面就是再来一个小循环,二叉树的层次遍历
* 下面我们再来看一个中序遍历
* @author Leon.Sun
*
*/
public class LinkedBinaryTree implements BinaryTree {
private Node root;
// private int size;
public LinkedBinaryTree(Node root) {
super();
this.root = root;
}
public LinkedBinaryTree() {
super();
}
@Override
public boolean isEmpty() {
return root==null;
}
@Override
public int size() {
System.out.println("二叉树节点的个数: ");
return this.size(root);
}
private int size(Node root) {
if(root==null) {
return 0;
}else {
int nl = this.size(root.leftChild);
int nr = this.size(root.rightChild);
return nl+nr+1;
}
}
@Override
public int getHeight() {
System.out.println("二叉树的高度是: ");
return this.getHeight(root);
}
private int getHeight(Node root) {
if(root==null) {
return 0;
}else {
int nl = this.getHeight(root.leftChild);
int nr = this.getHeight(root.rightChild);
return nl>nr ? nl+1 : nr+1;
}
}
/**
* 这里只传了值,没有说在哪里找
*/
@Override
public Node findKey(int value) {
/**
* 那我们在用户调用的时候显示的在root里面找
*
* 最后返回的是Node,如果没有找到就返回Null
* 找到就返回这个节点就可以了,
*/
return this.findKey(value, root);
}
/**
* 这里要写成Object
*
* 我们来读一下这个代码什么含义
* @param value
* @param root
* @return
*/
public Node findKey(Object value,Node root) {
/**
* 如果root等于空,直接返回null
* 如果你这颗树是空的,那你就返回空了
* 这个root是谁,刚开始的时候root是1,
* 但是后来最终是作为递归调用的一个结束条件的,
* 你看下面会一直递归调用的
*
* 这个root刚开始指的是1,整个树的根
* 最终到了左孩子和右孩子的根了
*
* 这是递归结束条件1
*
*/
if(root == null){
/**
* root为null,节点为空
* 可能是整棵树的根节点,
* 也可能是递归调用中的叶子节点的左孩子和右孩子
*/
return null;
/**
* 这是递归结束条件2
* 有可能是值,也可能是null
* 都有可能
*/
}else if(root != null && root.value == value){
/**
* 这个根不等于空,根的值等于value,这什么意思啊,
* 就是找到了,你不是找7吗,找到7了,
* 你找2,2这个节点不等于空,但是值是不是等于我们要找的2
* 找到了怎么办,找到了就直接返回了
* 这个大家记住了,如果不是这两种情况的话
* 那就该递归了
*
* 这是找到了
*/
return root;
}else {
/**
* 对左子树进行查找
* 所以root一直往下调用,最后root会变成所有叶子节点的
* 左孩子和右孩子都是空的,到叶子节点的时候就结束了
*
* 先在左子树里面找,再在右子树里面找
* 找到左子树里面的一个值,再找到右子树里面的一个值
*
* 这是递归调用
*/
Node node1 = this.findKey(value, root.leftChild);
/**
* 对右子树进行查找
*/
Node node2 = this.findKey(value, root.rightChild);
/**
* 如果左子树不等于空,值等于那返回就可以了
* 如果左子树里面找到了,就返回左子树里面的
*/
if(node1 != null && node1.value == value){
return node1;
}else if(node2 != null && node2.value == value){
/**
* 如果右子树里面找到了,那就返回右子树里面的
*/
return node2;
}else{
/**
* 如果左子树和右子树都没有找到,那还是返回空吧
*/
return null;
}
}
}
@Override
public void preOrderTraverse() {
if(root!=null) {
System.out.print(root.value + " ");
if(root.leftChild!=null) {
BinaryTree leftTree = new LinkedBinaryTree(root.leftChild);
leftTree.preOrderTraverse();
}
if(root.rightChild!=null) {
BinaryTree rightTree = new LinkedBinaryTree(root.rightChild);
rightTree.preOrderTraverse();
}
}
}
@Override
public void inOrderTraverse() {
System.out.println("中序遍历");
this.inOrderTraverse(root);
System.out.println();
}
private void inOrderTraverse(Node root) {
if(root!=null) {
if(root.leftChild!=null) {
this.inOrderTraverse(root.leftChild);
}
System.out.print(root.value + " ");
if(root.rightChild!=null) {
this.inOrderTraverse(root.rightChild);
}
}
}
@Override
public void postOrderTraverse() {
System.out.println("后序遍历");
this.postOrderTraverse(root);
System.out.println();
}
@Override
public void postOrderTraverse(Node node) {
if(node!=null) {
if(node.leftChild!=null) {
this.postOrderTraverse(node.leftChild);
}
if(node.rightChild!=null) {
this.postOrderTraverse(node.rightChild);
}
System.out.print(node.value + " ");
}
}
/**
* 不采用递归可以采用栈,栈是后进的先出
* 对于栈我们之前使用过一个例子
* 什么例子啊,十进制转换为二进制数,
* 是不是符合后进先出
* 现在这个列子与他类似
*
* 功能已经实现了,但是代码是什么含义啊
* 第一步理解他,第二步实现它就可以了
*
*
*/
@Override
public void inOrderByStack() {
System.out.println("中序非递归遍历:");
// 创建栈
/**
* Deque什么意思,Deque这个单词在JAVA里面是作为栈来使用的
* 实际上还是LinkedList,但是它是作为栈来使用的,
* 回顾我们的栈和队列,Deque是双端队列,栈操作建议使用他
* 一般我们当做栈来用的,但是他的实现类有两个,一个是找LinkedList
* 还有一个采用ArrayDeque,这都是可以的,再复习一下前面的内容
*
* 我么先看第一条语句是什么,是一个栈,是一个链栈,
* 为了简单起见,我们画一个数组类型的吧,
* 栈里面是可以放元素,就这么来放,首先我们把中序的顺序写出来
* 中序的顺序是什么,我们看顺序是怎么一步一步出来的
* 我们下边来写是不是一致,
* 第一步是先创建一个栈,一个链栈
* 为了简单起见我们写成一个数组的样式
*
*/
Deque stack = new LinkedList();
/**
* 我们这里又定义了一个变量
* 简单的就画到这儿,这个变量就叫current
* 因为我们没有画栈内存和堆内存
* 所以我们就简单的画,在这个方法的栈内存里面实现的
* root赋给current什么意思,current是不是指向root了
*
*/
Node current = root;
/**
* 如果current不等于空,他指向1
* 或者栈不等于空,现在栈是空的
* 你看这里是或者,两个条件只要满足一个就可以了
* 现在满足吧,现在不等于空啊
* 他的循环有两部分,前面有一个循环,后面是一个判断
*
* 又到这里了,current现在是空吗,不是空
* 栈现在是空吗,也不是空,还有一个1呢
*
* current已经不指向5了,他指向5的右孩子了
* 但是栈里面还不是空的,这里面还有一个1呢,
*
*/
while (current != null || !stack.isEmpty()) {
/**
* 前面的循环条件是谁啊,就是current != null这个条件
*
* 当current不等于空
*
* 如果current不等于空,current现在等于空,
* current现在是空的,就不循环了
*
* 循环又回来了,current不等于空,等于2
* 如果current不等于空,2不等于空
* 是不是我们现在要做这么一个操作,把我们的2放进去
*
*/
while (current != null) {
/**
* 我们是中序遍历
* 什么叫中序,一上来不会遍历这个根,
* 先把根存起来
* 栈里面有个1,先存起来
*
* 把4入栈
*
* 5已经进来了
*
* 把我们的2放进去
*
* 然后把3给放进去,3不等于空再放进去
* 这里是3吗,
*/
stack.push(current);
/**
* 然后干什么呢,然后把它的左孩子赋给current
* 这什么意思,current就指向4了,
* 指向4就回来,回来什么意思,
* 4等于空吗,不等于空
*
* 再取4的左孩子,4没有左孩子了,
* 如果4这边还有左孩子,它是想干什么
* 把它所有的左孩子一直放进去,一直往里头放
* 目前我们比较简单,只有这两级,
* 按照我们的中序遍历,整个的左边遍历完之后才能轮到root
* 所以我们进栈的顺序正好相反,1先进,4后进
* 退的时候4要先出来,后进先出的用栈
* 先进先出的用队列,那现在找4的孩子对不起他已经是空了
* 这个循环就结束了,从左边开始,一直找
* 所有的左孩子都进去了
*
* 5现在有左孩子吗,现在是空,
* 所以这个循环到这里就结束了,只把5放进去
*
* 然后再找他的左孩子,2的左孩子循环的过程中是不是又指向3了
*
* 3还有没有左孩子,3没有左孩子了,这个循环是不是结束了
* 再往下就不讲了,大家想一下,2进了栈,3进了栈,
* 和1进了栈,4进了栈,是不是一样的,他都一样的,
* 只不过当时是把1看成根的,现在是把2看成根的
* 重复刚才的过程就可以,总体下来是什么样的
* 不管是大树还是小的二叉树来说,都是先把左边的遍历完,
* 再遍历根,然后再遍历右边的,你看我们把451都出来了
* 右边变成一个整体开始处理了,这就是我们讲的非递归的遍历
* 代码我们做相关的比较的话,这个代码有几行,
* 在看看那个代码有几行,递归的代码少,然后递归的代码更容易理解
* 非递归的代码双重循环,还有这么多的条件,
* 这个要好好理解一下,采用递归可以简化思路,简化代码
* 但是递归调用每次调用都要开辟一份空间,他里面是比较占用空间的
* 关于中序非递归遍历就写到这,那非递归的前序和后序遍历怎么写呢,
* 大家可以自己来想,或者从网上找一些资料
* 可以把这一块给解决一下,提高不只是写代码的能力,
* 还有读代码的能力,还有思想,遇到问题该怎么来解决
* 到这儿的话我们再来看,那关于树和二叉树的所有内容,就都给大家讲了
* 二叉树是我们数据结构的一个重点
*
*/
current = current.leftChild;
}
/**
* 后面的条件是谁啊,!stack.isEmpty()这个条件
*
* 如果这个栈不等于空,栈现在是空的吗,现在不是空
* 怎么办
*
* 我们这里可不是循环,是if,就执行一遍
*
* 如果栈不等于空,怎么办,谁出栈啊,5出栈
*
* 如果stack不等于空,现在还有1呢,
*/
if (!stack.isEmpty()) {
/**
* 出栈,4出栈了,还是赋给current,
* 是不是没有变,
*
* 把这个1出栈,1出栈了,
* 出栈以后赋给current
* current现在又指向这个1了
*/
current = stack.pop();
/**
* 输出一下current的值,值4
*
* 输出5,5就这么出来了
*
* 输出current的值,他的值是1
* 这个时候发现对于我们这个图来说,左子树已经遍历完了
* 根也已经遍历完了,剩下来该右子树了
*/
System.out.print(current.value + " ");
/**
* 然后就是做一件事,因为按照我们的遍历来说
* 左边的一大串遍历完和1没有关系
* 这做了一个操作,4已经出去了
* 然后输出一下4的值,current现在指向4的右孩子
* 这是谁,是指向5了
*
* 把current的右孩子赋给他,相当于5是根
* 根已经遍历,是不是要遍历他的右了
* 5已经出来了,但是这里的5没有右孩子
* 没有的话if就到这儿了,5已经出去了
*
* 输出1之后current的rightChild是谁,
* 我们再在这里画一个栈
* 这个栈1和5都已经出去了
* 现在current指向1,他的右孩子,是2
* current指向2,右孩子是2了
*
*/
current = current.rightChild;
}
}
System.out.println();
}
@Override
public void preOrderByStack() {
}
@Override
public void postOrderByStack() {
}
/**
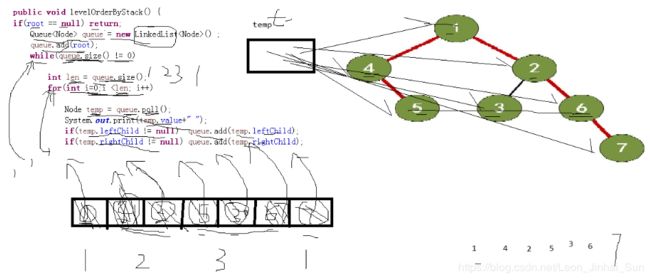
* 我们先来看按照层次遍历
* 先明确一下,他没有递归,
* Queue是什么来的,Queue是队列
*
* 体会一下队列的作用,我们把这棵树移过来
* 我们画一下这整个的执行过程,是怎么来执行的
* 开始执行了
*/
@Override
public void levelOrderByStack() {
/**
* 你如果想省事的话在这里加一条语句
* 加一条什么语句啊,按照层次遍历二叉树
*/
System.out.println("按照层次遍历二叉树");
/**
* 如果root等于null return什么意思,
* 没有递归,如果你的树是空树,就结束了,
* 如果要是不是空的呢,创建了一个队列
*/
if(root == null) return;
/**
* LinkedList是一个什么队列,是一个链表队列
* 我们在这里画一个数组,实际上是一个链表,你看这时候会发生什么,
*/
Queue queue = new LinkedList() ;
/**
* 告诉我这条语句是什么,是往队列里面加了一个节点
* root是谁啊,root就是1,先把这个1加进来了
*
*/
queue.add(root);
/**
* 当这个队列的数量不等于0,现在队列的长度是1
* 不等于空,获得了这个队列的长度,长度不就是1吗
*
* 再回到这边来,queue.size等于0吗
* 不等于0,等于几,等于3,等于3的话怎么办
* queue.size等于0吗,不等于0等于几
* 等于1的,数量是1
*
* 现在queue的数量等于0,循环结束
*
*/
while(queue.size() != 0)
{
/**
* 然后我们回头看queue.size等于0吗
* 不等于0等于几,等于2,有两个
* 得到他的数量是几啊,是2
*
* 获得这个值3,
*
* 数量是1,
*/
int len = queue.size();
/**
* 循环了几次,长度是几就循环了几次
* 你现在长度是1就循环了一次
* 这个for循环就循环一次,因为一开始是1
* 除了输出这个1之外,还把他的孩子放在里面了
* 然后这个循环就结束了
*
* 循环两次,怎么循环两次,
* 第一次处理4,第二次处理2
* i=0的时候我们先处理4,
* 第二次循环2
* 把第二个遍历完之后,之后他同时做了一件事
* 一件事做完了,把第三层所有的节点都放在里面去了,
* 并且是按照从左到右的顺序放的
* 放到队列里面去了,那就是先进先出了
*
* 循环三次
* 第一次处理5,第二次处理3,第三次处理6
* 怎么处理
*
* 然后再循环第二次,要处理3了,
*
* 再循环最后一次,第三次该处理这个6
* 这三次已经执行完了
* 他把第三层的执行完之后,同时第四层的所有节点已经在队列里面了
*
* 循环一次,
*/
for(int i=0;i
package com.learn.btree;
/**
* 在这个测试类里面我们要干什么,
* 这是一个测试类,我们按照这些功能依次来实现
* @author Leon.Sun
*
*/
public class Test {
public static void main(String[] args) {
Node node5 = new Node(5,null,null);
Node node4 = new Node(4,null,node5);
Node node3 = new Node(3,null,null);
Node node7 = new Node(7,null,null);
Node node6 = new Node(6,null,node7);
// Node node6 = new Node(6,null,null);
Node node2 = new Node(2,node3,node6);
Node node1 = new Node(1,node4,node2);
BinaryTree btree = new LinkedBinaryTree(node1);
// BinaryTree btree = new LinkedBinaryTree();
System.out.println(btree.isEmpty());
/**
* 前面我们实现了二叉树的三种遍历
* 都是采用递归来实现的,
*/
System.out.println("先序遍历:");
btree.preOrderTraverse();
System.out.println();
// System.out.println("中序遍历:");
btree.inOrderTraverse();
btree.postOrderTraverse();
/**
* 中序遍历非递归
* 中序遍历如果采用非递归的遍历
* 需要借助栈
*
* 我们再实现一个功能,这个非递归的我们先等一等吧
* 我们先看一下别的
*
* 还有一个中序遍历,非递归的方式来实现,这个需要借助栈
* 这三个我们就不写代码了,直接把代码拿过来运行出结果
* 然后我们一起来读这段代码
*
* 中序非递归遍历,里面有输出语句
*/
btree.inOrderByStack();
/**
* 按照层次遍历,借助队列
* 先把这些层次记住
*
* 另外还有一个层次遍历,不能用递归借助队列来实现
*
* 按照层次遍历,显示第一层,然后再是第二层,
* 1425367,是不是他,按照层次是这么来的
* 先第一层,第二层,第三层,第四层,
* 每层从左向右,看结果对不对
* 1425367,实现了
*
*/
btree.levelOrderByStack();
/**
* 在二叉树中查找某个值
*
* 第一个在二叉树中查找某个值
* 怎么样查到这个值,我们可以在遍历的基础上来实现查找
*
* 现在在二叉树中查找某个值,输出一下呗
* 我们要找个值是7,请问咱们的二叉树有没有7,
* 是有的,二叉树里面是有7的,是别的也可以,
* 我们看能不能够找到
*
* 返回的值是7,左孩子是空,右孩子也是空,是叶子节点
* 我们来找一下1,1是谁啊,1是根,node1的值是1
* 左孩子是4,左孩子还有孩子,右孩子是2,这功能已经实现了
* 我们可以debug,看到btree有左孩子,右孩子
* 然后值是1,那我们再来看他的左孩子,左孩子没有左孩子,只有右孩子
* 它的值是4,是不是可以看得到,再找他的右孩子呢,
* 没有左孩子也没有右孩子,他的值是5,我们都是可以这么来看到的,
* 要通过eclipse的调试工具来查看相关的一个内容
*
*/
System.out.println(btree.findKey(1));
/**
* 对于二叉树的高度以及二叉树的节点数量呢,我们有通过递归去实现了
* 大家发现递归非常的简单,另外递归使用的场合还是比较多的
* 这是我们讲的一个内容,再往下我们还有三个操作
*/
System.out.println(btree.getHeight());
System.out.println(btree.size());
}
}

