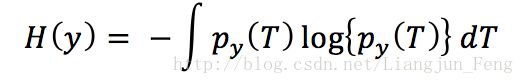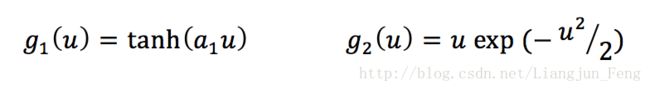机器学习教程 之 独立成分分析:PCA的高阶版
有好些天没写博客了,最近一直忙着在看论文,解模型,着实有点头痛。今天趁着又到周末了更一帖(其实是模型解不下去了…),这次来说一下一个在信号分析与数据挖掘领域颇为使实用的算法,独立成分分析(ICA),这个算法的求解方式会让人决定新奇而有所启发,可能会给你带来新的思路,这一篇算法已经有很多大神写过了,比如:
http://blog.csdn.net/neal1991/article/details/45128193
http://blog.csdn.net/u013802188/article/details/40923749
我在这里略作补充,说一下自己的见解,有不合适的地方欢迎大家指出
- ICA的起源与最初的目标
- 独立成分分析的经典假设
- 中心极限定理的解释——非高斯即独立!
- 独立成分分析无法确定的因素
- 独立成分分析的数据预处理
- ICA问题的经典解法,FastICA
- python-sklearn中的FastICA应用实例
一、ICA的起源与最初的目标
独立成分分析最初所希望解决的是极为复杂与困难的鸡尾酒问题:
在一场鸡尾酒舞会上,有两个人在同时讲话,在房间的不同位置有两个麦克风,而每个麦克风记录下的是两个人声音的混合。问题是:如何利用麦克风的混合声音信息来获得每个讲话者所说的话。
现在我们用x1,x2表示我们观测到的混合声音,s1,s2表示说话者发出的源信号,称为独立成分,则我们可以将鸡尾酒问题表示为
转化为矩阵表示为
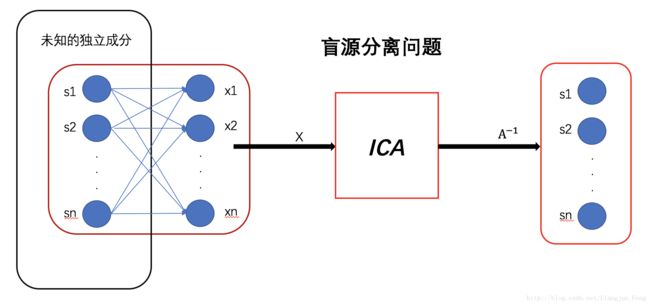
其中的A表示混合信号是由独立成分线性组合成的,称A为混合矩阵。通过上式我们可以发现我们需要通过已知的X去推导未知的混合矩阵A和S,这是非常困难的,事实上,如果没有后续强有力的假设,鸡尾酒问题根本无法求解,因为我们不知道关于原独立成分S的任何信息,鸡尾酒这一类问题也被抽象称为盲源分离问题。
二、独立成分分析的经典假设
在上一节中已经说明,如果不做出一些强有力的假设和分析,是无法直接求解盲源分离问题的,为了实现独立成分分析,ICA给出了一下三个假设条件
- 各个成分之间是相互统计独立的
这是ICA的一个最基本也是最重要的原则,非常有趣的是一旦给出了这个假设,我们便可以通过一定的方式求解这个模型。对此的解释是,如果任意的随机变量序列(x1,x2,…,xn)之间是相互统计独立的,则这就意味着我们不能从其余的变量中获得随机变量xj的任何信息。
随机变量之间的独立性可以通过概率密度来精确刻画,用p(x1,x2,…,xn)表示xi之间的联合概率密度,当xi之间满足下列等式的时候,我们就说,xi是相互统计独立的

- 独立成分是服从非高斯分布的
ICA要求随机变量服从非高斯分布的原因在于,高斯分布的随机变量就有高阶累积量为零的特性,而对于独立成分分析而言,高阶信息是实现独立成分分析的本质因素。一般的在标准的独立成分分析中最多只允许有一个成分服从高斯分布,因此我们也经常可以使用ICA作为一种去除高斯噪声的手段 - 假设混合矩阵A是方阵
这一假设是对于标准的独立成分分析而言,这一假设意味着独立成分的个数等于观测信号的个数,从而进一步假设混合矩阵A是可逆的,这可以使得计算简化,求混合矩阵A等价于求它的逆矩阵,原独立信号S可以通过下式得到

当做出一场三个假设之后,我们便可以求解混合矩阵A还有独立成分X,也就是说独立成分分析是可实现的。对于第三个假设,在一些改进算法中可以适当放宽
三、中心极限定理的解释——非高斯即独立!
本文中将要给出的一种ICA模型的解法是基于非高斯性极大化的思想来进行求解的,这里首先描述一下这种解法的思路:
在概率论中,有一个被称为中心极限定理的经典结果,其内容十分简洁明了,是说,在一定条件下,相互统计独立的随机变量的和的分布趋向于高斯分布。对于这一定理,我们可以这样理解,两个相互统计独立的随机变量的和比其中任何一个参与求和的随机变量更加靠近高斯分布。对于标准的独立成分分析模型,独立成分的估计可以通过寻找混合变量正确的线性组合来实现,为了估计一个独立成分,我们考虑观测信号xi的线性组合,有下式
其中bi是我们需要求解的混合向量,又在上式中将x以s表示,我们可以得到
通过这一公式,我们可以看出,如果bT是混合矩阵A的逆矩阵的某一行时,则线性组合bTx实际上就是一个独立成分,因此,在向量q中只能有一个元素为1,其余元素均值为0。同时,又因为qTs = bTx,我们可以求解最优向量b使得bTx的非高斯性极大化,此时的y便为我们所求的独立成分,而为了达到这一目的,我们必须有一种度量随机变量非高斯性的度量,在我们即将讲述的FastICA算法中,使用的是负熵这标准,对于负熵这一概念,我会在讲解FastICA的第六章节详细介绍
四、独立成分分析无法确定的因素
尽管我们建立了盲源分离问题的数学模型,同时还针对模型给出了一系列充分的假设,但是仍然有一些因素是无法在求解过程中确定的
- 不能确定独立成分的方差(能量)
原因是很明显的,由于混合矩阵和独立成分都是未知的,如果对独立成分乘上某个标量ai != 0,同时对混合矩阵相应的列除以一个相同的标量ai,则不影响混合信号的值

因此在独立成分分析算法中,可以固定独立成分的方差,由于独立成分是随机变量,则最自然的方法就是假设独立成分具有单位方差,即E(si^2) = 1,在实际构造这个算法时,往往会考虑这个约束,但这仍不能确定每个独立成分的符号,这是因为当每个独立成分都乘-1后不改变原有模型 - 不能确定独立成分的顺序
我们可以通过一个置换矩阵来具体说明这个问题,假设P是一个置换矩阵,

这时矩阵Ps就是新的独立成分,他只是与原先的独立成分具有不同的排列顺序。相应的矩阵A(P-1)就是新的混合矩阵,同样的它的每一列只是与矩阵A具有不同的顺序
当然,在独立成分分析的绝大多数应用中,这两个不确定性并不是十分重要,用ICA算法所得到的解能够满足相当多的实际应用,所得到的源信号的幅度和排序对于通常所考虑的问题影响不大,所以我们可以说独立成分分析所求的的解是波形保持解
这里从2000年Hyvarinen提出FastICA算法的论文中截取一些FastICA的应用案例,向大家说明独立成分分析的使用效果与原理
1、信号分离
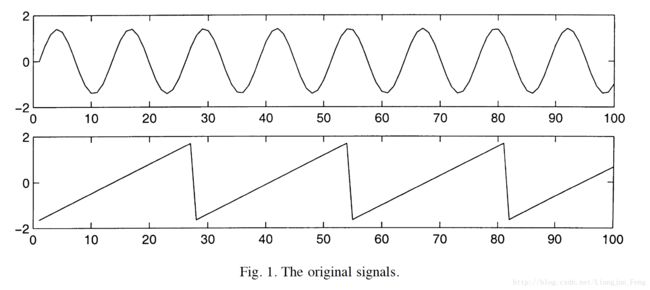
两组源信号
所观测的混合信号
FastICA分离信号
2、图像滤波
以上四张图从左到右,从上到下分别为:原图像、施加噪声的图像、使用ICA滤波的图像、使用稀疏编码滤波的图像
3、Hyvarinen对于ICA算法的描述
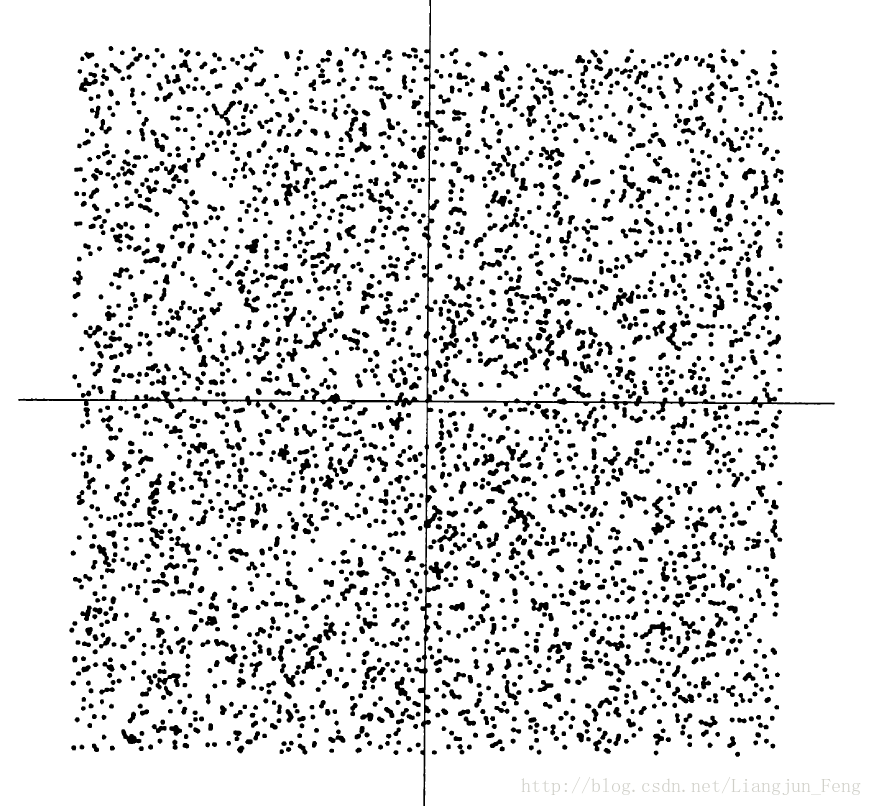
在论文中Hyvarinen这样描述他对ICA的理解,对于两组相互独立的随机变量,它们的联合分布如下
在上图的分布中,我们无法从一个点获得另一个点的任何信息。这两组随机分布点的线性叠加后的分布为
而我们使用ICA模型估计的混合矩阵A实际上就是由上图四边形的边所指向的方向所代表的向量组成,而两个高斯变量线性叠加后是怎样的呢?
它没有任何的边缘信息,因此,我们也就无从对混合矩阵A进行估计。使用ICA对两个非高斯变量解混之后我们可以得到如下
五、独立成分分析的数据预处理
数据的中心化
不失一般性的,我们可以假设混合变量和独立成分都是零均值的。这个假设在相当程度上简化了算法,如果零均值并不成立,我们可以通过预处理,即减去平均值,来达到这个条件。原始的观测混合数据x’可以通过下式进行预处理

这样,因为有
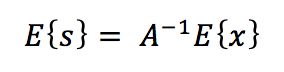
所以独立成分也是零均值的,混合矩阵在预处理前后保持不变,因此我们可以进行中心化而不影响混合矩阵的估计。对于零均值的数据,在用算法估计出混合矩阵和独立成分之后,剪掉的均值可以通过将(A-1)E{x’}加到零均值的独立成分上来进行重构数据白化
白化的随机向量y指的是它的各分量是不相关的,并且具有单位方差。换句话说,随机向量y的协方差矩阵是单位阵,即 E{yyT} = I,白化意味着我们将观测数据向量x进行线性变换 z = Vx ,使得新向量是白化的随机向量,白化有时也称为球化
白化变换有一种使用特征值分解(EVD)的简便方法,V的获取公式如下
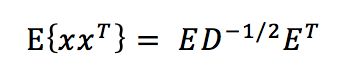
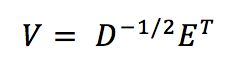
六、ICA问题的经典解法,FastICA
好了,说了这么多,我终于要开始介绍ICA模型的解法了,这里是用的是一种使用负熵作为非高斯性度量的定点迭代解法(敲黑板)
1、负熵
负熵是基于信息论中熵的概念,而随机变量的熵与它所给出的信息有关,随机变量越是没有结构,越无序,它的熵越大。密度函数为py(T)的随机变量y的熵定义为
则负熵定义为
其中ygauss表示服从高斯分布的随机变量,且与随机变量y具有相同的方差。信息论中的一个重要的结果是说,在所有相同方差的随机变量中,高斯随机变量具有最大的熵,因此,负熵总是非负的,当且仅当随机变量y服从高斯分布时,负熵为零。负熵作为非高斯性的度量是一个非常好的标准,因为它在某些判据下是非高斯性的最优估计器。但因为负熵的计算需要求累计分布,比较复杂,因此FastICA给出了负熵的估计式
2.FastICA的单个独立成分解法
我们首先说一下在混合矩阵A中,单个混合向量的求解过程,然后再给出多个混合向量同步求解的计算方法
1.选择一个初始随机向量W
2.使用 W(n+1) = E{xg(W(n)Tx)} - E{g'(W(n)Tx)}W(n)更新W
3.使用W = W/||W||使W方差单位化
4.如果没有收敛,则返回第二步
这里的收敛指得是W不在变化,更新后仍指向同一个方向,关于更新公式的求解方法,是从以非高斯性极大化为目标的目标函数通过拉格朗日乘子法与牛顿迭代法得到的,具体的推导这里不再赘述。上面迭代过程中使用的函数g()通常选用为
上式的a1常数取值为1~2
3.FastICA多个独立成分同时求解
FastICA多个独立同时求解,其实就是在迭代时同时对多个初始向量进行更新迭代。但要注意的一点是,为了避免有向量同时收敛到同一个最优值,在每次更新结束后,我们需要对得到的新向量做去相关操作,比较简单的方法是使用Gram-Schmidt-like正交化方法。到这里为止我们便可以实现对盲源分离问题的求解
七、python-sklearn中的FastICA应用实例
在python的sklearn库中有现成的FastICA函数,使用方式如下
from sklear.decomposition import FastICA #导入函数
ica = FastICA(conponents = 70) #conponents为独立元个数,如果不设置默认为训练的样本数
dataICA = ica.fit_transform(data) #拟合并转化数据为独立成分
dataICA2 = ica.transform(data2) #使用拟合好的ica转化另一份数据为独立成份将ICA用于语音分离的python实例代码:https://github.com/LiangjunFeng/Machine-Learning/blob/master/9.FastICA.py
语音数据下载地址:
语音1:https://github.com/LiangjunFeng/Machine-Learning/blob/master/pic/ICA/LDC2017S07.clean.wav
语音2:https://github.com/LiangjunFeng/Machine-Learning/blob/master/pic/ICA/LDC2017S10.scaled.wav
语音3:https://github.com/LiangjunFeng/Machine-Learning/blob/master/pic/ICA/LDC93S1.wav
语音4、语音5为噪声信号
初始信号、混合信号、FastICA分离信号依次为: