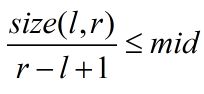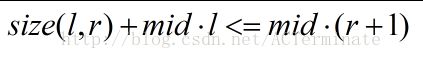HDU 6070 Dirt Ratio [二分+线段树]

题意：给n个数，设x/y为区间内不同数的个数除以区间长度，问x/y的最小值。

题解：二分答案x/y，当我们去检验mid的时候，会得到如下表达式（size表示区间不同数的个数）

之后我们对表达式进行转换

这样我们就可以根据如上表达式判断mid是否合法。我们每次枚举右端点，当新加入一个点的时候，我们需要对不包含这个数的最右的连续区间进行整体加1，这时候我们就可以，用线段树来维护区间最小值，线段树上的每一个叶子节点表示，size（l,r）+mid*l 。

AC代码：

#include
#include
#include
#define eps 1e-8
#define N 60005
using namespace std;
double tree[N*4],add[N*4];
int last[N];
int a[N];
void pushdown(int root)
{
    tree[root<<1]+=add[root];
    tree[root<<1|1]+=add[root];
    add[root<<1]+=add[root];
    add[root<<1|1]+=add[root];
    add[root]=0;
}
void update(int l,int r,int L,int R,int root,double k)
{
    if(l<=L&&R<=r)
    {
        tree[root]+=k;
        add[root]+=k;
        return ;
    }
    if(add[root]>eps)pushdown(root);
    int mid=L+R>>1;
    if(r<=mid)update(l,r,L,mid,root<<1,k);
    else if(l>mid)update(l,r,mid+1,R,root<<1|1,k);
    else
    {
        update(l,mid,L,mid,root<<1,k);
        update(mid+1,r,mid+1,R,root<<1|1,k);
    }
    tree[root]=min(tree[root<<1],tree[root<<1|1]);
}
double query(int l,int r,int L,int R,int root)
{
    if(l<=L&&R<=r)
        return tree[root];
    if(add[root]>eps)pushdown(root);
    int mid=L+R>>1;
    if(r<=mid)return query(l,r,L,mid,root<<1);
    else if(l>mid)return query(l,r,mid+1,R,root<<1|1);
    else return min(query(l,mid,L,mid,root<<1),query(mid+1,r,mid+1,R,root<<1|1));
    tree[root]=min(tree[root<<1],tree[root<<1|1]);
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        double l=0,r=1.0;
        for(int g=0;g<20;g++)
        {
            double mid=(l+r)/2.0;
            memset(tree,0,sizeof(tree));
            memset(add,0,sizeof(add));
            memset(last,0,sizeof(last));
            int flag=0;
            for(int i=1;i<=n;i++)
            {
                update(last[a[i]]+1,i,1,n,1,1);
                update(i,i,1,n,1,mid*i);
                last[a[i]]=i;
                double k=query(1,i,1,n,1);
                if(k<=(double)mid*(i+1))
                {
                    flag=1;break;
                }
            }
            if(flag!=1)l=mid;
            else r=mid;
        }
        printf("%.4f\n",r);
    }
}