【Python机器学习及实践】基础篇：无监督学习经典模型（特征降维）

Python机器学习及实践——基础篇：无监督学习经典模型（特征降维）

特征降维不仅可以重构有效的低维度特征向量，同时也为数据展现提供了可能。在特征降维的方法种，主成分分析（Principal Component Analysis, PCA）是最为经典和实用的特征降维技术，特别是辅助图像识别方法有突出的表现。

---

1.主成分分析

线性相关矩阵秩计算样例

import numpy as np

# 初始化一个2*2的线性相关矩阵
M = np.array([[1, 2], [2, 4]])
# 计算2*2线性相关矩阵的秩
print(np.linalg.matrix_rank(M, tol=None))

PCA的思想是首先把原来的特征空间做了映射，使得新的映射后特征空间数据彼此正交。这样一来，通过主成分分析就尽可能保留下具备区分性的低维数据特征。

应用案例：手写体数字图像识别

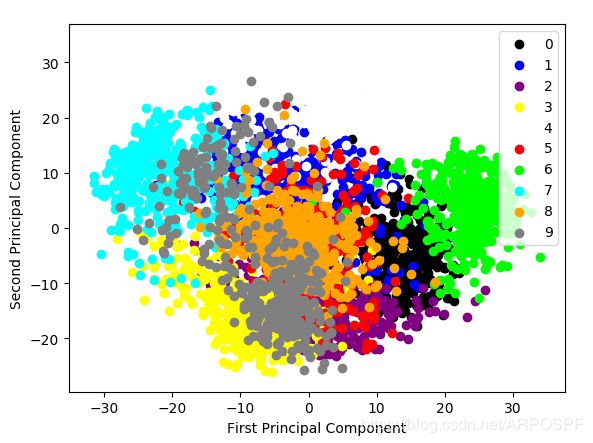
显示手写体数字图片经PCA压缩后的二维空间分布

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
@File  : PCAdigits.py
@Author: Xinzhe.Pang
@Date  : 2019/7/23 20:05
@Desc  : 
"""
import pandas as pd
import numpy as np

# 从互联网读入手写体图片识别任务的训练数据
digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra',
                           header=None)
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes',
                          header=None)
# 分割训练数据的特征向量和标记
X_digits = digits_train[np.arange(64)]
y_digits = digits_train[64]

# 从sklearn.decomposition导入PCA
from sklearn.decomposition import PCA

# 初始化一个可以将高维度特征向量（64维）压缩到2个维度的PCA
estimator = PCA(n_components=2)
X_pca = estimator.fit_transform(X_digits)

# 显示10类手写体数字图像经过PCA压缩后的2维空间分布
from matplotlib import pyplot as plt


def plot_pca_scatter():
    colors = ['black', 'blue', 'purple', 'yellow', 'white', 'red', 'lime', 'cyan', 'orange', 'gray']

    for i in range(len(colors)):
        px = X_pca[:, 0][y_digits.as_matrix() == i]
        py = X_pca[:, 1][y_digits.as_matrix() == i]
        plt.scatter(px, py, c=colors[i])

    plt.legend(np.arange(0, 10).astype(str))
    plt.xlabel('First Principal Component')
    plt.ylabel('Second Principal Component')
    plt.show()


plot_pca_scatter()

使用原始像素特征和经PCA压缩重建的低维特征，在相同配置的支持向量机（分类）模型上分别进行图像识别。

# 对训练数据、测试数据进行特征向量（图片像素）与分类目标的分割。
X_train = digits_train[np.arange(64)]
y_train = digits_train[64]
X_test = digits_test[np.arange(64)]
y_test = digits_test[64]

# 导入基于线性核的支持向量机分类器
from sklearn.svm import LinearSVC

# 使用默认参数的LinearSVC,对原始64维像素特征的训练数据进行建模，并在测试数据上做出预测
svc = LinearSVC()
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)

# 使用PCA将64维图像数据压缩到20个维度
estimator = PCA(n_components=20)

# 利用训练特征决定（fit）20个正交维度的方向，并转化（transform）原训练特征
pca_X_train = estimator.fit_transform(X_train)

# 对测试特征进行同样处理
pca_X_test = estimator.transform(X_test)

# 使用默认参数的LinearSVC对压缩后的20维特征的训练数据进行建模，并在测试数据上进行预测
pca_svc = LinearSVC()
pca_svc.fit(pca_X_train, y_train)
pca_y_pred = pca_svc.predict(pca_X_test)

原始像素特征与PCA压缩重建的低维特征，在相同配置的支持向量机（分类）模型上识别性能的差异。

# 从sklearn.matrics导入classification_report用于更加细致的分类性能分析
from sklearn.metrics import classification_report

# 对使用原始图像高维像素特征训练的支持向量机分类器的性能做出评估
print(svc.score(X_test, y_test))
print(classification_report(y_test, y_pred, target_names=np.arange(10).astype(str)))

# 对使用PCA压缩重建的低维图像特征训练的支持向量机分类器的性能做出评估
print(pca_svc.score(pca_X_test, y_test))
print(classification_report(y_test, pca_X_test, target_names=np.arange(10).astype(str)))

降维/压缩问题则是选取数据具有代表性的特征，在保持数据多样性（Variance）的基础上，规避掉大量的特征冗余和噪声，不过这个过程也很有可能会损失一些有用的模式信息。