机器学习常用算法模型总结
文章目录
- 1.基础篇:了解机器学习
-
- 1.1 什么是机器学习
- 1.2 机器学习的场景
-
- 1.2.1 模式识别
- 1.2.2 数据挖掘
- 1.2.3 统计学习
- 1.2.4 自然语言处理
- 1.2.5 计算机视觉
- 1.2.6 语音识别
- 1.3 机器学习与深度学习
- 1.4 机器学习和人工智能
- 1.5 机器学习的数学基础
-
- 特征值和特征向量的定义
- 2. 算法模型篇
-
- 2.1 线性回归模型
-
- 2.1.1 什么是线性回归模型?
- 2.1.2 一元线性回归
-
- 数学原理
- 知识点:最小二乘法
- 代码实现一元线性回归
- 2.1.3 线性回归模型评估
-
- R-squared
- Adj.R-squared
- P值
- 过拟合与欠拟合
- 2.1.4 多元线性回归以及案例
- 2.2 逻辑回归模型
-
- 2.2.1 Sigmoid激活函数
- 逻辑回归案例分析
- 2.3 决策树模型
-
- 2.3.1决策树的基本原理
- 2.3.2 决策树的建树依据
-
- 基尼系数
- 信息熵
- 2.3.3 决策树剪枝策略
- 2.4 朴素贝叶斯模型
-
- 2.4.1 朴素贝叶斯的算法原理
- 2.4.2 一维特征变量下的贝叶斯模型
- 2.4.3 二维特征变量下的贝叶斯模型
- 2.4.4 N维特征变量下的贝叶斯模型
- 2.5 K近邻(KNN算法)
-
- 2.5.1 K近邻算法的基本原理
- 2.5.2 K近邻算法的计算步骤
- 2.5.3 k值的选取
- 2.5.4 数据标准化
- 2.6 支持向量机(SVM)
-
- 2.6.1 初识SVM
- 2.6.2 SVM的工作原理
- 2.6.3 硬间隔、软间隔和非线性SVM
-
- 高斯核函数:利用相似度来变换特征
- 2.6.4 用SVM如何解决多分类问题
-
- (1) 一对多法
- (2) 一对一法
- 2.6.5 总结
- 2.6.6 优缺点
- 2.7 K-means算法
-
- 2.7.1 经典k-means算法描述
- 2.7.2 优缺点
- 2.7.3 K-means算法的调优与改进
- (1) 数据预处理
- (2) 合理选择 K 值
- 2.7.4 三种改进算法
- (1)k-means++
- (2) 采用核函数
- (3)ISODATA
- 2.7.5 DBSCAN算法
-
- 基本概念
- 工作流程
- 优缺点
- 2.8 EM算法
-
- 2.8.1. 思想
- 2.8.2. 举例
- 2.8.3. 推导
- 2.8.5. 应用
- 2.9 随机森林
-
- 2.9.1 集成模型简介
- 2.9.2 Bagging算法
- 2.9.3 Boosting算法
- 2.9.4 Stacking模型
- 2.9.5 随机森林模型的基本原理
- 2.9.6 数据随机
- 2.9.7 特征随机
- 2.10 AdaBoost
-
- 2.10.1 AdaBoost算法的核心思想
- 2.10.2 AdaBoost算法的数学原理
- 2.10.3 补充知识:正则化项
- 2.11 GBDT、XGBoost、LightGBM
1.基础篇:了解机器学习
1.1 什么是机器学习
机器学习是把人类思考归纳的过程转化为计算机通过对数据的处理计算得出模型的过程。经过计算机得出的模型能够以近似于人的方式解决很多复杂的问题。
从广义上来说,机器学习通过赋予机器学习的能力,让其完成直接编程无法完成的功能。但从实践的意义上来说,机器学习是一种通过利用数据,训练模型,然后使用模型进行预测的一种方法。
人类在成长、生活过程中积累了很多历史经验(数据),然后对这些经验进行“归纳”,获得了“规律”(模型)。当遇到未知的问题或者需要对未来进行“推测”时,就会使用这些“规律”,对未知问题进行“推测”(预测),从而指导自己的生活和工作。
机器学习中的“训练”与“预测”过程,可以对应到人类的“归纳”和“推测”过程。通过这样的对应,我们发现机器学习的思想并不复杂,仅仅是对人类学习成长的一个模拟。由于机器学习不是基于编程形成的结果,因此它的处理过程不是因果的逻辑,而是通过归纳思想得出的相关性结论。
我们举个例子,支付宝春节的“集五福”活动,用手机扫“福”字照片自动识别福字。支付宝先给计算机提供大量“福”字的照片数据,通过算法模型训练,系统不断学习,然后输入一张新的福字照片,机器就能自动识别这张照片是否含有福字,这就是用了机器学习。
机器学习是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论、计算机科学等多门学科。机器学习的概念就是通过输入海量训练数据对模型进行训练,使模型掌握数据所蕴含的潜在规律,进而对新输入的数据进行准确的分类或预测。其过程如下图所示:

1.2 机器学习的场景
机器学习跟模式识别、统计学习、数据挖掘、计算机视觉、语音识别、自然语言处理等领域有着很深的联系。
从范围上来说,机器学习跟模式识别、统计学习、数据挖掘相类似。同时,机器学习与其他领域结合,形成了计算机视觉、语音识别、自然语言处理等多种交叉学科。因此,一般说数据挖掘,可以等同于说机器学习。同时,我们常说的机器学习应用的场景,是指通用场景,不局限在结构化数据,还有图像、音频等领域的应用。
下图是与机器学习相关的应用领域:
1.2.1 模式识别
模式识别 = 机器学习
两者的主要区别在于前者是从工业界发展起来的概念,后者则源自计算机学科。在著名的《Pattern Recognition And Machine Learning》这本书中,Christopher M. Bishop在开头是这样说的“模式识别源自工业界,而机器学习来自于计算机学科。不过,它们中的活动可以被视为同一个领域的两个方面,同时在过去的10年间,它们都有了长足的发展”。
1.2.2 数据挖掘
数据挖掘 = 机器学习+数据库。
近些年,数据挖掘的概念实在过于火爆,几乎等同于炒作。但凡说数据挖掘都会吹嘘数据挖掘如何如何,例如从数据中挖出金子,以及将废弃的数据转化为价值等等。但是,尽管可能会挖出金子,但也可能挖到的是“石头”。这个说法的意思是,数据挖掘仅仅是一种思考方式,告诉我们应该尝试从数据中挖掘出知识,但不是每个数据都能挖掘出金子的,所以不要神话它。一个系统绝对不会因为上了一个数据挖掘模块就变得无所不能(这是IBM最喜欢吹嘘的),恰恰相反,一个拥有数据挖掘思维的人员才是关键,而且他还必须对数据有深刻的认识,这样才可能从数据中导出模式指引业务的改善。大部分数据挖掘中的算法是机器学习的算法在数据库中的优化。
1.2.3 统计学习
统计学习 ≈ 机器学习。
统计学习是与机器学习高度重叠的学科。因为机器学习中的多数方法来自统计学,甚至可以认为,统计学的发展促进机器学习的繁荣。例如著名的支持向量机算法,就源自统计学科。但是在某种程度上两者是有分别的,这个分别在于:统计学习者重点关注的是统计模型的发展与优化,偏数学,而机器学习者更关注的是能够解决问题,偏实践。因此,机器学习人员会重点研究学习算法在计算机上执行的效率与准确性。
1.2.4 自然语言处理
自然语言处理 = 机器学习+文本处理。
自然语言处理技术,是让机器理解人类的语言的一门领域。在自然语言处理技术中,大量使用编译原理相关的技术,例如词法分析,语法分析等。除此之外,在理解这个层面,则使用了语义理解、机器学习等技术。作为唯一由人类自身创造的符号,自然语言处理一直是机器学习界不断研究的方向。按照百度机器学习专家余凯的说法“听与看,说白了就是阿猫和阿狗都会的,而只有语言才是人类独有的”。如何利用机器学习技术进行自然语言的深度理解,一直是工业和学术界关注的焦点。
1.2.5 计算机视觉
计算机视觉 = 机器学习+图像处理。
图像处理技术,将图像处理为适合机器学习模型中的输入。机器学习则负责从图像中识别出相关的模式。计算机视觉相关的应用非常的多,例如OCR识图、手写字符识别、车牌识别等等应用。这个领域是应用前景非常火热的,同时也是研究的热门方向。随着机器学习的新领域深度学习的发展,大大促进了计算机图像识别的效果,因此未来计算机视觉界的发展前景不可估量。
常用的学习数据集:CIFAR-10
1.2.6 语音识别
语音识别 = 机器学习+语音处理。
语音识别就是音频处理技术与机器学习的结合。语音识别技术一般不会单独使用,一般会结合自然语言处理的相关技术。目前的相关应用有苹果的语音助手siri等。
1.3 机器学习与深度学习
近来,机器学习的发展产生了一个新的方向——深度学习。
虽然深度学习听起来颇为高大上,但其理念却非常简单,就是传统的神经网络发展到了多隐藏层的情况。
在上面介绍过,自90年代以后,神经网络消寂了一段时间。但是BP算法的发明人Geoffrey Hinton一直没有放弃对神经网络的研究。由于神经网络在隐藏层扩大到两个以上,其训练速度会非常慢,因此实用性一直低于支持向量机。2006年,Geoffrey Hinton在科学杂志《Science》上发表了一篇文章,论证了两个观点:
- 多隐层的神经网络具有优异的特征学习能力,学习得到的特征对数据有更本质的刻画,从而有利于可视化或分类;
- 深度神经网络在训练上的难度,可以通过逐层初始化来有效克服。
通过这样的发现,不仅解决了神经网络在计算上的难度,同时也说明了深层神经网络在学习上的优异性。从此,神经网络重新成为了机器学习界主流的学习技术。同时,具有多个隐藏层的神经网络被称为深度神经网络,基于深度神经网络的学习研究称之为深度学习。
由于深度学习的重要性,在各方面都取得极大关注,按照时间轴排序,有以下四个标志性事件值得一说:
- 2012年6月,《纽约时报》披露了Google Brain项目,这个项目由Andrew Ng和Map-Reduce发明人Jeff Dean共同主导,用16000个CPU Core的并行计算平台,训练一种称为“深层神经网络”的机器学习模型,在语音识别和图像识别等领域获得了巨大的成功。
- 2012年11月,微软在中国天津的一次活动上公开演示了一个全自动的同声传译系统,讲演者用英文演讲,后台的计算机一气呵成自动完成语音识别、英中机器翻译,以及中文语音合成,效果非常流畅,其中支撑的关键技术是深度学习;
- 2013年1月,在百度年会上,创始人兼CEO李彦宏高调宣布要成立百度研究院,其中第一个重点方向就是深度学习,并为此而成立深度学习研究院(IDL)。
- 2013年4月,《麻省理工学院技术评论》杂志将深度学习列为2013年十大突破性技术(Breakthrough Technology)之首。
机器学习是通过人工提取特征,而深度学习是真正学习什么样的特征才是最合适的,学习一个如何提取特征的过程。
深度学习属于机器学习的子类。基于深度学习的发展极大的促进了机器学习的地位提高,更进一步地推动了业界对机器学习的父类人工智能梦想的重视。
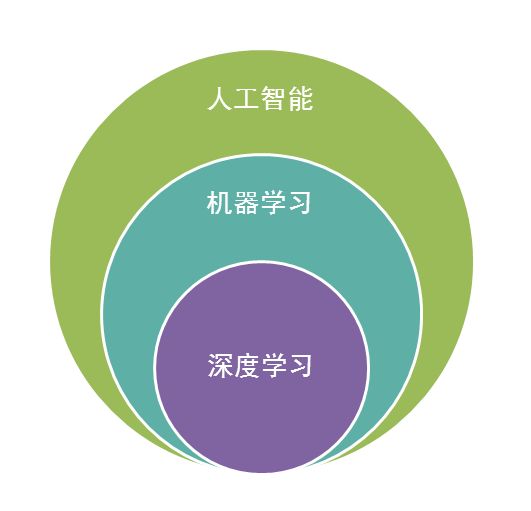
1.4 机器学习和人工智能
人工智能是机器学习的父类,深度学习则是机器学习的子类。如果把三者的关系用图来表明的话,则是下图:
毫无疑问,人工智能(AI)是人类所能想象的科技界最突破性的发明。从某种意义上说,人工智能就像游戏最终幻想的名字一样,是人类对于科技界的最终梦想。从50年代提出人工智能的理念以后,科技界,产业界在不断探索。甚至各种小说、电影都在以各种方式展现对于人工智能的想象。人类可以发明类似于人类的机器,这是多么伟大的理念!但事实上,自从50年代以后,人工智能的发展就磕磕碰碰,未有见到足够震撼的科学技术进步。
总结起来,人工智能的发展经历了如下若干阶段,从早期的逻辑推理,到中期的专家系统,这些科研进步确实使我们离机器的智能有点接近了,但还有一大段距离。直到机器学习诞生以后,人工智能界感觉终于找对了方向。基于机器学习的图像识别和语音识别在某些垂直领域达到了跟人相媲美的程度。机器学习使人类第一次如此接近人工智能的梦想。
1.5 机器学习的数学基础
机器学习理论篇1:机器学习的数学基础 - 知乎 (zhihu.com)
-
注意特征值和特征向量
特征值(eigenvalue)和特征向量(eigenvector)具有共同前缀 eigen- ,其起源于德语,意为“特征”。首先我们应该充分理解“特征”的含义:对于线性代数而言,特征向量和特征值体现了矩阵的本质,“特征”强调了单个矩阵的特点,相当于它的ID card。
从线性代数的角度出发,如果把矩阵看作n维空间下的一个线性变换,这个变换有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。其中的N个变化方向,就是这个矩阵最重要的“特征”。
有了特征的概念后,我们又如何理解特征值与特征向量呢?可以作这样比喻:
- 如果把矩阵看作是位移,那么特征值 = 位移的速度,特征向量 = 位移的方向。
- 特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定(注意观察定义式)。特征值大于1,所有属于此特征值的特征向量变长;特征值属于(0, 1),特征向量缩短;特征值小于0,特征向量则反向延长。
我们都知道线性代数中,左乘一个矩阵是对应着行变换,右乘一个矩阵对应列变换,其实际的作用也就是对常规坐标系进行了迁移。那么,
对于在普通二维坐标系下的向量X,它在矩阵A描述空间中的表示与自己单纯的进行拉伸或者缩放的效果一致,满足这种特殊性的X就是特征矩阵,对应的拉伸量$\lambda $就是特征值。
有了这个特殊的性质,特征向量与特征值出现在很多有矩阵运算的地方,如主成分分析(PCA)、奇异值分解(SVD)等机器学习方法中更是时常提到。
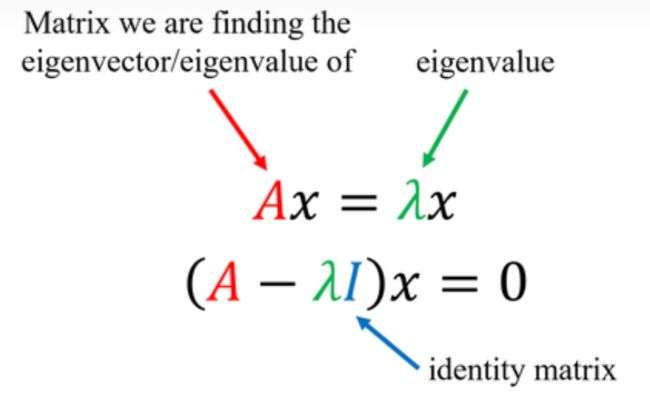
特征值和特征向量的定义
设A是n阶矩阵,如果存在常数 λ 和n维非零向量X,
使得 AX=λX
则称λ为矩阵A的一个特征值(标量),X为矩阵A对应于特征值的一个特征向量( n×1 )
该式子可理解为向量在几何空间中经过矩阵A的变换后得到向量 λX 。由此可知,向量 X经过矩阵A变换后,只是大小伸缩了 λ 倍。总而言之:特征向量提供了复杂的矩阵乘法到简单的数乘之间的转换!
- 并且,我们有以下推论:
- A k X = λ k X A^kX=λ^kX AkX=λkX
- A − 1 X = 1 / λ X A^{-1}X=1/\lambda X A−1X=1/λX
- A = W ∑ W T A=W\sum W^T A=W∑WT
其中第三个是特征值分解公式,W为n×n的特征向量矩阵(n个大小为 n×1 的特征向量 X组成)。 Σ 是包含对应特征值的对角矩阵。根据不同的特征值的大小,可以知道每个特征向量对应权重,即其重要性。
其中I是单位矩阵,因此|λ�−�|称为A的特征多项式。详细见维基百科:Eigenvalues and eigenvectors - Wikipedia
2. 算法模型篇
2.1 线性回归模型
2.1.1 什么是线性回归模型?
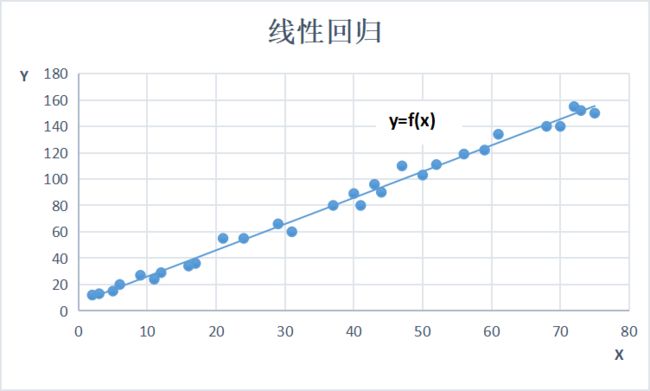
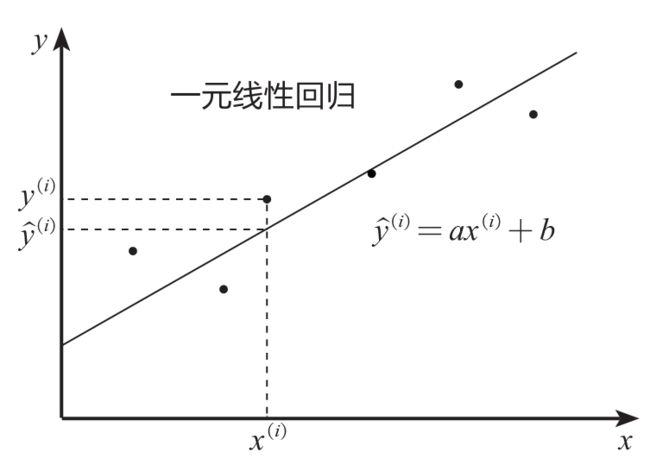
线性回归模型,是利用线性拟合的方式探寻数据背后的规律。如下图所示,先通过搭建线性回归模型寻找这些散点(也称样本点)背后的趋势线(也称回归曲线),再利用回归曲线进行一些简单的预测分析或因果关系分析。
在线性回归中,根据特征变量(也称自变量)来预测反应变量(也称因变量)。根据特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归。例如,通过“工龄”这一个特征变量来预测“薪水”,就属于一元线性回归;而通过“工龄”+“行业”+“所在城市”等多个特征变量来预测“薪水”,就属于多元线性回归。
2.1.2 一元线性回归
数学原理
一元线性回归模型又称为简单线性回归模型,其形式可以表示为如下所示的公式:y=ax+b
其中,y为因变量,x为自变量,a为回归系数,b为截距。
如下图所示, y ( i ) {y}^{(i)} y(i) 为实际值, y ^ ( i ) \hat{y}^{(i)} y^(i) 为预测值,一元线性回归的目的就是拟合出一条线来使得预测值和实际值尽可能接近,如果大部分点都落在拟合出来的线上,则该线性回归模型拟合得较好。
那如何衡量实际值与预测值的接近程度呢?在数学上通过两者差值的平方和(又称残差平方和)来进行衡量,公式如下:
∑ ( y ( i ) − y ^ ( i ) ) 2 \sum({y}^{(i)}-\hat{y}^{(i)})^{2} ∑(y(i)−y^(i))2
在机器学习领域,残差平方和又称回归模型的损失函数。
显然残差平方和越小,实际值和预测值就越接近。而数学上求最小值的方法为求导数,当导数为0时,残差平方和最小。我们将残差平方和换一个表达形式,公式如下:
∑ ( y ( i ) − ( a x i + b ) ) 2 \sum({y}^{(i)}-(a{x}^i+b))^{2} ∑(y(i)−(axi+b))2
对上述公式进行求导,然后令其导数为0,便可求得一元线性回归模型的回归系数a和截距b。以上便是一元线性回归的数学原理,数学上称为最小二乘法。在Python中,有专门的库来求解回归系数a和截距b,不需要我们去计算复杂的数学公式。
知识点:最小二乘法
以如下数据为例演示最小二乘法,供大家参考:
{ x = [ 1 , 2 , 3 ] y = [ 3 , 4 , 5 ] \begin{cases} x = [1, 2, 3] \\ y = [3, 4, 5] \end{cases} {x=[1,2,3]y=[3,4,5]
假设线性回归模型的拟合方程为y=ax+b,那么残差平方和(损失函数)可以定义成如下所示的公式:
L = ∑ i = 1 m ( y i − ( a x i + b ) ) 2 L = \sum_{i=1}^m(y^i-(ax^i+b))^2 L=i=1∑m(yi−(axi+b))2
拟合的目的是使残差平方和尽可能地小,即实际值和预测值尽可能地接近。根据高等数学中求极值的相关知识,通过对残差平方和进行求导(对a和b进行求导),导数为0时,该残差平方和将取极值,此时便能获得拟合需要的系数a和截距b了。
根据高等数学中复合求导的知识可知f’(g(x))=f’(x)g’(x),又因为x2的导数为2x,所以(g(x))2的导数为2g(x)g’(x),分别对a和b求导,得到如下公式。
{ ①对 a 求导 ∑ i = 1 m 2 ( y i − ( a x i + b ) ) 2 x i = 0 ②对 b 求导 ∑ i = 1 m 2 ( y i − ( a x i + b ) ) 2 = 0 \begin{cases} ①对a求导 \\ \sum_{i=1}^m2(y^i-(ax^i+b))^2x^i = 0 \\ ②对b求导 \\ \sum_{i=1}^m2(y^i-(ax^i+b))^2 = 0 \end{cases} ⎩ ⎨ ⎧①对a求导∑i=1m2(yi−(axi+b))2xi=0②对b求导∑i=1m2(yi−(axi+b))2=0
将x和y的值代入且等号两边同除以2,得到:
{ ( 3 − ( a + b ) ) × 1 + ( 4 − ( 2 a + b ) ) × 2 + ( 5 − ( 3 a + b ) ) × 3 = 0 ( 3 − ( a + b ) ) + ( 4 − ( 2 a + b ) ) + ( 5 − ( 3 a + b ) ) = 0 \begin{cases} (3-(a+b))×1 + (4-(2a+b))×2 + (5-(3a+b))×3 = 0 \\ (3-(a+b)) + (4-(2a+b)) + (5-(3a+b)) = 0 \end{cases} {(3−(a+b))×1+(4−(2a+b))×2+(5−(3a+b))×3=0(3−(a+b))+(4−(2a+b))+(5−(3a+b))=0
简化如下:
{ 26 − 14 a − 6 b = 0 12 − 6 a − 3 b = 0 \begin{cases} 26-14a-6b = 0 \\ 12-6a-3b = 0 \end{cases} {26−14a−6b=012−6a−3b=0
求解:
{ a = 1 b = 2 \begin{cases} a = 1 \\ b = 2 \end{cases} {a=1b=2
也就是说拟合曲线为y=x+2,可以发现完美拟合了3个点,感兴趣的读者可以验证一下,此时的残差平方和的确取最小值,且为0。对于多元线性回归,其各个系数和截距的推导方法和上面是一致的,只不过变成了多元方程组而已。
看不懂也没关系,使用Python可直接进行求解。
代码实现一元线性回归
通过Python的Scikit-Learn库可以轻松搭建一元线性回归模型。
下面通过构造学生的学习时间和考试成绩的数据,来讲解如何在Python中搭建一元线性回归模型。
step1:构造数据
from collections import OrderedDict
import pandas as pd
examDict = {
'学习时间': [0.50, 0.75, 1.00, 1.25, 1.50, 1.75, 1.75, 2.00, 2.25,
2.50, 2.75, 3.00, 3.25, 3.50, 4.00, 4.25, 4.50, 4.75, 5.00, 5.50],
'分数': [10, 22, 13, 43, 20, 22, 33, 50, 62,
48, 55, 75, 62, 73, 81, 76, 64, 82, 90, 93]
}
examOrderDict = OrderedDict(examDict)
exam = pd.DataFrame(examOrderDict)
# 查看数据格式
print(exam.head())
# 输出:
# 学习时间 分数
# 0 0.50 10
# 1 0.75 22
# 2 1.00 13
# 3 1.25 43
# 4 1.50 20
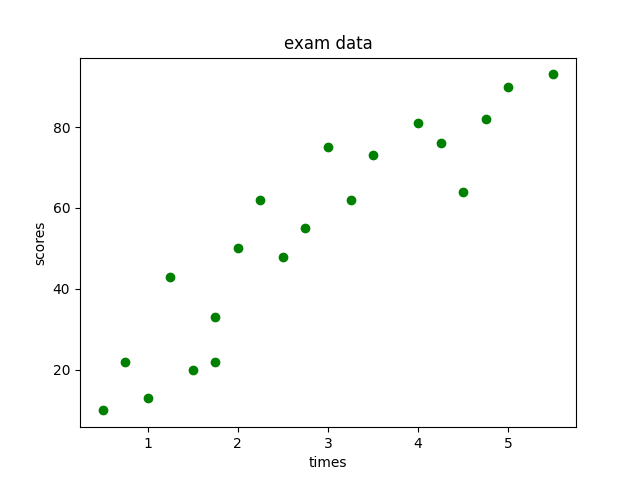
step2:绘制散点图
利用Matplotlib库绘制散点图,代码如下:
import matplotlib.pyplot as plt
exam_X = exam['学习时间']
exam_Y = exam['分数']
plt.scatter(exam_X, exam_Y, color = 'green')
plt.ylabel('scores')
plt.xlabel('times')
plt.title('exam data')
plt.show()
结果如下:
step3:划分数据集
将样本数据随机划分为训练集和测试集,代码如下:
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(exam_X,
exam_Y,
train_size = 0.8)
# 查看分割后的结果
print(X_train.head())
print(X_train.shape)
step4:搭建模型
引入Scikit-Learn库可快速搭建线性回归模型,代码如下:
X_train = X_train.values.reshape(-1, 1)
X_test = X_test.values.reshape(-1, 1)
#从skl中导入线性回归的模型
from sklearn.linear_model import LinearRegression
#创建模型
model = LinearRegression()
#训练模型
model.fit(X_train, Y_train)
用fit()函数完成模型搭建,此时的model就是一个搭建好的线性回归模型。
step5:模型预测
接着就可以利用搭建好的模型model来预测数据。假设自变量是1.5,那么使用predict()函数就能预测对应的因变量y,代码如下:
print(model.predict([[1.5]]))
输出:[31.90969141]
step6:模型可视化
将搭建好的模型以可视化的形式展示出来,代码如下:
import matplotlib.pyplot as plt
#绘制散点图
plt.scatter(exam_X, exam_Y, color = 'green', label = 'train data')
#设定X,Y轴标签和title
plt.ylabel('scores')
plt.xlabel('times')
#绘制最佳拟合曲线
Y_train_pred = model.predict(X_train)
plt.plot(X_train, Y_train_pred, color = 'black', label = 'best line')
#来个图例
plt.legend(loc = 2)
plt.show()
效果如下:
step7:构造线性回归方程
a = model.intercept_
b = model.coef_
a = float(a)
b = float(b)
print('该模型的线性回归方程为y = {} + {} * x'.format(a, b))
该模型的线性回归方程为:y = 7.821319018404893 + 16.57464212678937 * x
2.1.3 线性回归模型评估
模型搭建完成后,还需要对模型进行评估,通常以3个值对模型进行评估:R-squared(即统计学中的 R 2 R^2 R2 ),Adj.R-squared(即Adjuested R 2 R^2 R2 )、P值。其中R-squared和Adj.R-squared用来衡量线性拟合的优劣,P值用来衡量特征变量的显著性。
R-squared
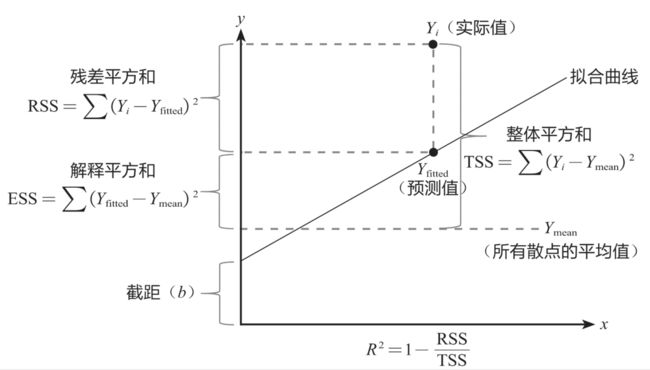
要想理解R-squared,得先了解3组概念:整体平方和TSS、残差平方和RSS、解释平方和ESS,它们的关系如下图所示:
其中 Y i Y_i Yi 为实际值, Y f i t t e d Y_{fitted} Yfitted 为预测值, Y m e a n Y_{mean} Ymean 为所有散点的平均值, R 2 R^2 R2 为R-squared值。
对于一个拟合度较高的线性回归模型,实际值要尽可能落在拟合曲线上,即残差平方和RSS尽可能小,根据R-squared的计算公式 R 2 = 1 − ( R S S / T S S ) R^2 = 1-(RSS/TSS) R2=1−(RSS/TSS) ,也就是希望R-squared尽可能大。当RSS趋向于0时,说明实际值基本都落在了拟合曲线上,模型的拟合程度非常高,此时R-squared趋向于1,所以在实战中,R-squared越接近1,模型的拟合程度越高。
不过模型的拟合程度也不是越高越好,拟合程度过高可能会导致过拟合现象(过拟合下面会介绍)。
其计算公式如下:
整体平方和: T S S = ∑ ( Y i − Y m e a n ) 2 TSS = \sum(Y_i - Y_{mean})^2 TSS=∑(Yi−Ymean)2
残差平方和: R S S = ∑ ( Y i − Y f i t t e d ) 2 RSS = \sum(Y_i - Y_{fitted})^2 RSS=∑(Yi−Yfitted)2
解释平方和: E S S = ∑ ( Y f i t t e d − Y m e a n ) 2 ESS = \sum(Y_{fitted} - Y_{mean})^2 ESS=∑(Yfitted−Ymean)2
R-squared值: R 2 = 1 − R S S T S S R^2 = 1 - \frac{RSS}{TSS} R2=1−TSSRSS
Adj.R-squared
Adj.R-squared是R-squared的改进版,其目的是为了防止选取的特征变量过多而导致虚高的R-squared。每新增一个特征变量,线性回归背后的数学原理都会都会导致R-squared增加,但是这个新增的特征变量可能对模型并没有什么帮助。为了限制过多的特征变量,引入了Adj.R-squared的概念,它在R-squared的基础之上,额外考虑了特征变量的数量这一因素,其公式如下:
R ˉ 2 = 1 − ( 1 − R 2 ) ( n − 1 ) n − k − 1 \bar{R}^2 = 1 - \frac{(1-R^2)(n-1)}{n-k-1} Rˉ2=1−n−k−1(1−R2)(n−1)
其中n为样本数量,k为特征变量数量。从公式可以看出,k越大,会对Adj.R-squared产生负面影响,从而制约数据建模的人不要为了追求R-squared值而添加过多的特征变量。当考虑了特征变量数量后,Adj.R-squared就能够更准确的反映线性模型的拟合程度。
P值
P值涉及统计学中假设检验中的概念,其假设特征变量与目标变量无显著相关,P值是当原假设为真时,所得到的的样本观察结果或更极端结果出现的概率。如果概率越大,即P值越大,原假设为真的可能性越大,即无显著相关性的可能性越大;如果该概率越小,即P值越小,原假设为真的可能性就越小,即有显著相关性的可能性就越大。
所以,P值越小,显著相关性越大。
通常以0.05为阈值,当P值小于0.05时,就认为特征变量与目标变量显著相关。
过拟合与欠拟合
过拟合即过度拟合,指模型在训练过程中拟合程度过高,虽然它很好的贴合了训练数据集,但是丧失了泛化能力,不具备推广性,也就是说,如果换了训练集以外的数据就达不到较好的预测效果。与过拟合相对应的是欠拟合,欠拟合是指模型拟合程度不高,数据距离拟合线较远,或指模型没有很好的捕捉到数据特征,不能很好的拟合。
2.1.4 多元线性回归以及案例
多元线性回归的原理和一元线性回归的原理在本质上是一样的,不过因为多元线性回归可以考虑到多个因素对目标变量的影响,所以在实际应用中使用更为广泛。
y = k 0 + k 1 x 1 + k 2 x 2 + k 3 x 3 . . . y = k_0+k_1x_1+k_2x_2+k_3x_3... y=k0+k1x1+k2x2+k3x3...
其中x1、x2、x3……为不同的特征变量,k1、k2、k3……则为这些特征变量前的系数,k0为常数项。多元线性回归模型的搭建也是通过数学计算来获取合适的系数,使得如下所示的残差平方和最小,其中 y ( i ) {y}^{(i)} y(i) 为实际值, y ^ ( i ) \hat{y}^{(i)} y^(i) 为预测值。
∑ ( y ( i ) − y ^ ( i ) ) 2 \sum({y}^{(i)}-\hat{y}^{(i)})^{2} ∑(y(i)−y^(i))2
数学上依旧通过最小二乘法和梯度下降法来求解系数。具体步骤可参考最小二乘法知识点,这里主要讲解如何通过Python代码来求解系数。其核心代码和一元线性回归其实是一致的,具体如下:
from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X, Y)
上述代码和一元线性回归代码的区别在于这里的X包含多个特征变量信息。利用多元线性回归可以构建更加丰富和实用的模型,例如,根据工龄、地域、行业等因素来预测薪水,根据房屋大小、所处位置、是否靠近地铁等因素来预测房价等。
具体实战案例可参考客户价值预测模型
具体实例:客户价值预测模型
2.2 逻辑回归模型
线性回归模型是一种回归模型,它用于对连续变量进行预测,如预测收入范围、客户价值等。如果要对离散变量进行预测,则要使用分类模型。分类模型与回归模型的区别在于其预测的变量不是连续的,而是离散的一些类别,例如,最常见的二分类模型可以预测一个人是否会违约、客户是否会流失、肿瘤是良性还是恶性等。本文要学习的逻辑回归模型虽然名字中有“回归”二字,但其在本质上却是分类模型。
既然逻辑回归模型是分类模型,为什么名字里会含有“回归”二字呢?这是因为其算法原理同样涉及线性回归模型中的线性回归方程:
y = k 0 + k 1 x 1 + k 2 x 2 + k 3 x 3 + . . . y=k_0+k_1x_1+k_2x_2+k_3x_3+... y=k0+k1x1+k2x2+k3x3+...
上面这个方程是用于预测连续变量的,其取值范围为(-∞,+∞),而逻辑回归模型是用于预测类别的,例如,用逻辑回归模型预测某物品是属于A类还是B类,在本质上预测的是该物品属于A类或B类的概率,而概率的取值范围是0~1,因此不能直接用线性回归方程来预测概率,那么如何把一个取值范围是(-∞,+∞)的回归方程变为取值范围是(0,1)的内容呢?
首先通过似然函数,然后通过对数将其转化为对数相加形式,此时应用梯度上升求最大值,引入 θ = − 1 m l ( θ ) \theta=-\frac{1}{m}l(\theta) θ=−m1l(θ)转换为梯度下降任务
2.2.1 Sigmoid激活函数
这就需要用到下图所示的Sigmoid函数,它可将取值范围为(-∞,+∞)的数转换到(0,1)之间。下面我们来看一下Sigmoid函数的推导过程, y y y是之前提到的线性回归方程,取值范围是(-∞,+∞),那么指数函数 e y e^y ey 的取值范围是(0,+∞),再做一次变换, e y 1 + e y \frac{e^y}{1+e^y} 1+eyey 的取值范围就变成(0,1),然后分子分母同除以 e y e^y ey ,就得到了Sigmoid函数:
{ 将 ( − ∞ , + ∞ ) 转变为( 0 , 1 ) y = k 0 + k 1 x 1 + k 2 x 2 + k 3 x 3 + . . . ⟶ e y ⟶ e y 1 + e y ⟶ 1 1 + e − y ↓ ↓ ↓ ↓ ( − ∞ , + ∞ ) ( 0 , + ∞ ) ( 0 , 1 ) ( 0 , 1 ) \begin{cases} \quad\quad\quad\quad\quad\quad\quad\quad 将(-\infty, +\infty)转变为(0,1) \\ y= k_0+k_1x_1+k_2x_2+k_3x_3+... \longrightarrow e^y \longrightarrow \frac{e^y}{1+e^y} \longrightarrow \frac{1}{1+e^{-y}}\\ \quad\quad\quad\quad\quad\downarrow \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\downarrow \quad\quad\quad\quad\downarrow \quad\quad\quad\quad\downarrow\\ \quad\quad\quad(-\infty, +\infty) \quad\quad\quad\quad\quad\quad\quad (0, +\infty) \quad(0, 1) \quad\quad(0, 1) \\ \end{cases} ⎩ ⎨ ⎧将(−∞,+∞)转变为(0,1)y=k0+k1x1+k2x2+k3x3+...⟶ey⟶1+eyey⟶1+e−y1↓↓↓↓(−∞,+∞)(0,+∞)(0,1)(0,1)
总结来说,逻辑回归模型本质就是将线性回归模型通过Sigmoid函数进行了一个非线性转换,得到一个介于0~1之间的概率值,对于二分类问题(分类0和1)而言,其预测分类为1(或者说二分类中数值较大的分类)的概率可以用如下所示的公式计算:
P = 1 1 + e − ( k 0 + k 1 x 1 + k 2 x 2 + k 3 x 3 + . . . ) P = \frac{1}{1+e^{-(k_0+k_1x_1+k_2x_2+k_3x_3+...)}} P=1+e−(k0+k1x1+k2x2+k3x3+...)1
因为概率和为1,则分类为0(或者说二分类中数值较小的分类)的概率为1-P。
逻辑回归模型的本质就是预测属于各个分类的概率,有了概率之后,就可以进行分类了。对于二分类问题来说,例如在预测客户是否会违约的模型中,如果预测违约的概率P为70%,则不违约的概率为30%,违约概率大于不违约概率,此时就可以认为该客户会违约。对于多分类问题来说,逻辑回归模型会预测属于各个分类的概率(各个概率之和为1),然后根据哪个概率最大,判定属于哪个分类。
了解了逻辑回归模型的基本原理后,在实际模型搭建中,就是要找到合适的系数ki和截距项k0,使预测的概率较为准确,在数学中使用极大似然估计法来确定合适的系数ki和截距项k0,从而得到相应的概率。在Python中,已经有相应的库将数学方法整合好了,通过调用库中的模块就能建立逻辑回归模型,从而预测概率并进行分类。
逻辑回归案例分析
详细见:逻辑回归实现鸢尾花数据集分类
2.3 决策树模型
2.3.1决策树的基本原理
决策树模型是机器学习的各种算法模型中比较好理解的一种模型,它的基本原理是对一系列问题进行if/else的推导,最终实现相关决策。
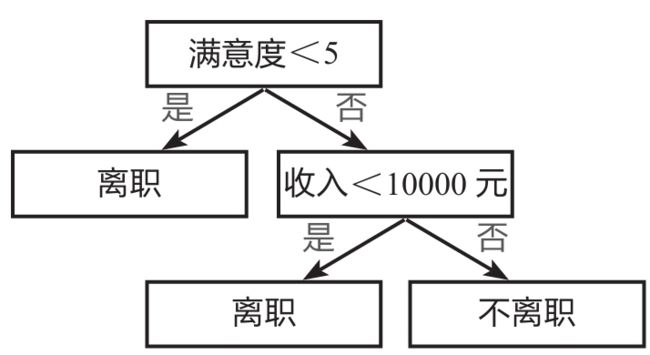
下图所示为一个典型的决策树模型——员工离职预测模型的简单演示。
该决策树首先判断员工满意度是否小于5,若答案为“是”,则认为该员工会离职,若答案为“否”,则接着判断该员工收入是否小于10000元,若答案为“是”,则认为该员工会离职,若答案为“否”,则认为该员工不会离职。
上图所示即决策树模型的核心原理,之后要讲解的员工离职预测模型是基于大数据搭建的一个稍复杂的模型。商业实战中不会仅根据“满意度”和“收入”两个特征来判断是否离职,而是根据多个特征来预测离职概率,再根据相应的阈值来判断是否离职,例如,离职概率超过50%即认为该员工会离职。
下面解释决策树模型的几个重要概念:父节点和子节点、根节点和叶子节点。
父节点和子节点是相对的,子节点由父节点根据某一规则分裂而来,然后子节点作为新的父节点继续分裂,直至不能分裂为止。根节点则和叶子节点是相对的,根节点是没有父节点的节点,即初始节点,叶子节点则是没有子节点的节点,即最终节点。决策树模型的关键就是如何选择合适的节点进行分裂。
在上图中,“满意度<5”是根节点,同时也是父节点,分裂成两个子节点“离职”和“收入<10000元”;子节点“离职”因为不再分裂出子节点,所以又是叶子节点;另一个子节点“收入<10000元”又是其下面两个节点的父节点;“离职”及“不离职”则为叶子节点。
在实际应用中,企业会通过已有的数据来分析离职员工都符合何种特征,如查看他们的满意度、收入、工龄、月工时、项目数等,然后选择相应的特征进行节点分裂,便能搭建出类似上面的决策树模型,再利用该模型预测员工离职情况,并根据预测结果采取应对措施。
决策树的概念并不复杂,主要是通过连续的逻辑判断得出最后的结论,其关键在于如何建立这样一棵“树”。例如,根节点应该选择哪一个特征,选择“满意度<5”或选择“收入<10000元”作为根节点,会收到不同的效果。其次,收入是一个连续变量,选择“收入<10000元”或选择“收入<100000元”作为一个节点,其结果也是有区别的。
2.3.2 决策树的建树依据
基尼系数
决策树模型的建树依据主要用到的是基尼系数的概念。基尼系数(gini)用于计算一个系统中的失序现象,即系统的混乱程度。基尼系数越高,系统的混乱程度就越高,建立决策树模型的目的就是降低系统的混乱程度,从而得到合适的数据分类效果。基尼系数的计算公式:
g i n i ( T ) = 1 − ∑ p i 2 gini(T) = 1 - \sum{p}^{2}_{i} gini(T)=1−∑pi2
其中 p i p_i pi为类别i在样本T中出现的频率,即类别为i的样本占总样本个数的比率;Σ为求和符号,即对所有的进行求和。
例如,一个全部都是离职员工的样本中只有一个类别——离职员工,其出现的频率是100%,所以该系统的基尼系数为 1 − 1 2 = 0 1-1^2=0 1−12=0 ,表示该系统没有混乱,或者说该系统的“纯度”很高。而如果样本中一半是离职员工,另一半是未离职员工,那么类别个数为2,每个类别出现的频率都为50%,所以其基尼系数为 1 − ( 0. 5 2 + 0. 5 2 ) = 0.5 1-(0.5^2 + 0.5^2) = 0.5 1−(0.52+0.52)=0.5 ,即其混乱程度很高。
当引入某个用于分类的变量(如“满意度<5”)时,分类后的基尼系数公式:
g i n i ( T ) = S 1 S 1 + S 2 g i n i ( T 1 ) + S 2 S 1 + S 2 g i n i ( T 2 ) gini(T) = \frac{S_1}{S_1+S_2}gini(T_1)+\frac{S_2}{S_1+S_2}gini(T_2) gini(T)=S1+S2S1gini(T1)+S1+S2S2gini(T2)
其中S1、S2为划分后的两类各自的样本量,gini(T1)、gini(T2)为两类各自的基尼系数。
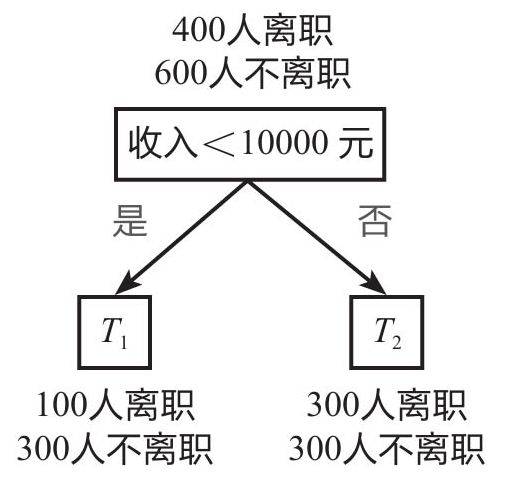
例如,一个初始样本中有1000个员工,其中已知有400人离职,600人不离职。划分前该系统的基尼系数为1-(0.42+0.62)=0.48,下面采用两种方式决定根节点:一是根据“满意度<5”进行分类;二是根据“收入<10000元”进行分类。
划分方式1: 以“满意度<5”为根节点进行划分,如下图所示,划分后的基尼系数为0.3,计算过程如下:
T 1 T_1 T1 的基尼系数: g i n i ( T 1 ) = 1 − ( 1 2 + 0 2 ) = 0 gini(T_1) = 1 - (1^2 + 0^2) = 0 gini(T1)=1−(12+02)=0
T 2 T_2 T2 的基尼系数: g i n i ( T 2 ) = 1 − ( 0.25 2 + 0.75 2 ) = 0.375 gini(T_2) = 1 - ({0.25}^2 + {0.75}^2) = 0.375 gini(T2)=1−(0.252+0.752)=0.375
划分后的基尼系数:
g i n i ( T ) = 200 + 0 200 + 0 + 200 + 600 × 0 + 200 + 600 200 + 0 + 200 + 600 × 0.375 = 0.3 gini(T) = \frac{200+0}{200+0+200+600} \times 0 + \frac{200+600}{200+0+200+600} \times 0.375 = 0.3 gini(T)=200+0+200+600200+0×0+200+0+200+600200+600×0.375=0.3
划分方式2: 以“收入<10000元”为根节点进行划分,如下图所示,划分后的基尼系数为0.45,计算过程如下:
T 1 T_1 T1 的基尼系数: g i n i ( T 1 ) = 1 − ( 0.2 5 2 + 0.7 5 2 ) = 0.375 gini(T_1) = 1 - (0.25^2 + 0.75^2) = 0.375 gini(T1)=1−(0.252+0.752)=0.375
T 2 T_2 T2 的基尼系数: g i n i ( T 2 ) = 1 − ( 0.5 2 + 0.5 2 ) = 0.5 gini(T_2) = 1 - ({0.5}^2 + {0.5}^2) = 0.5 gini(T2)=1−(0.52+0.52)=0.5
划分后的基尼系数:
g i n i ( T ) = 100 + 300 100 + 300 + 300 + 300 × 0.375 + 300 + 300 100 + 300 + 300 + 300 × 0.5 = 0.45 gini(T) = \frac{100+300}{100+300+300+300} \times 0.375 + \frac{300+300}{100+300+300+300} \times 0.5 = 0.45 gini(T)=100+300+300+300100+300×0.375+100+300+300+300300+300×0.5=0.45
可以看到,划分前的基尼系数为0.48,以“满意度<5”为根节点进行划分后的基尼系数为0.3,而以“收入<10000元”为根节点进行划分后的基尼系数为0.45。
基尼系数越低表示系统的混乱程度越低,区分度越高,越适合用于分类预测,因此这里选择“满意度<5”作为根节点。
上面演示了如何利用基尼系数来选择根节点,根节点下面的节点也是用类似方法来选择。例如,对于变量“收入”来说,是选择“收入<10000元”还是选择“收入<100000元”作为划分依据,同样通过计算这两种情况下划分后的基尼系数来进行判断。若还有其他变量,如工龄、月工时等,也是通过类似方法计算划分后的基尼系数,再根据基尼系数判断如何划分节点,从而搭建出一个较为完善的决策树模型。
采用基尼系数进行运算的决策树也称为CART决策树。
信息熵
除了基尼系数,还有一种衡量系统混乱程度的经典手段——信息熵。
在搭建决策树模型时,信息熵的作用和基尼系数是基本一致的,都可以帮助我们合理地划分节点。信息熵H(X)的计算公式如下:
H ( X ) = − ∑ p i l o g 2 ( p i ) H(X) = -\sum{p}_i{log}_2(p_i) H(X)=−∑pilog2(pi)
其中X表示随机变量,随机变量的取值为 X 1 、 X 2 、 X 3 . . . X_1、X_2、X_3... X1、X2、X3... ,在n分类问题中便有n个取值,例如,在员工离职预测模型中,X的取值就是“离职”与“不离职”两种; p i p_i pi 表示随机变量X取值为 X i X_i Xi 的发生频率,且有 ∑ p i = 1 \sum{p}_i = 1 ∑pi=1 。需要注意的是,公式中的对数函数是以2为底的。
举例来说,一个全部都是离职员工的样本中只有一个类别——离职员工,其出现的频率是100%,所以该系统的信息熵为 − 1 × l o g 2 1 = 0 -1×log_21=0 −1×log21=0 ,表示该系统没有混乱。而如果样本中一半是离职员工,另一半是未离职员工,那么类别个数为2,每个类别出现的频率都为50%,所以该系统的信息熵为 − ( 0.5 × l o g 2 0.5 + 0.5 × l o g 2 0.5 ) = 1 -(0.5 \times {log}_2{0.5}+0.5 \times {log}_2{0.5}) = 1 −(0.5×log20.5+0.5×log20.5)=1 ,表示该系统混乱程度很高。
当引入某个用于进行分类的变量A(如“满意度<5”),则根据变量A划分后的信息熵又称为条件熵,其计算公式如下:
H A ( X ) = S 1 S 1 + S 2 H ( X 1 ) + S 2 S 1 + S 2 H ( X 2 ) H_A(X)= \frac{S_1}{S_1+S_2}H(X_1) + \frac{S_2}{S_1+S_2}H(X_2) HA(X)=S1+S2S1H(X1)+S1+S2S2H(X2)
其中 S 1 、 S 2 S_1、S_2 S1、S2 为划分后的两类各自的样本量, H ( X 1 ) 、 H ( X 2 ) H(X_1)、H(X_2) H(X1)、H(X2) 为两类各自的信息熵。
为了衡量不同划分方式降低信息熵的效果,还需要计算分类后信息熵的减少值(原系统的信息熵与分类后系统的信息熵之差),该减少值称为熵增益或信息增益,其值越大,说明分类后的系统混乱程度越低,即分类越准确。信息增益的计算公式如下:
G a i n ( A ) = H ( X ) − H A ( X ) Gain(A) = H(X) - H_A(X) Gain(A)=H(X)−HA(X)
继续用前面讲解基尼系数时的例子来讲解信息熵的应用。初始样本有1000个员工,其中已知有400人离职,600人不离职。划分前该系统的信息熵为 − ( 0.4 × l o g 2 0.4 + 0.6 × l o g 2 0.6 ) = 0.97 -(0.4×log_20.4+0.6×log_20.6)=0.97 −(0.4×log20.4+0.6×log20.6)=0.97 ,混乱程度较高。下面采用两种方式决定根节点:一是根据“满意度<5”进行分类;二是根据“收入<10000元”进行分类。
划分方式1: 以“满意度<5”为根节点进行划分,如下图所示,划分后的信息熵为0.65,信息增益为0.32,计算过程如下:
初始信息熵: H ( X ) = − ( 0.4 × l o g 2 0.4 + 0.6 × l o g 2 0.6 ) = 0.97 H(X) = - (0.4\times{log}_2{0.4}+0.6\times{log}_2{0.6}) = 0.97 H(X)=−(0.4×log20.4+0.6×log20.6)=0.97
X 1 X_1 X1 的信息熵: H ( X 1 ) = − ( 1 × l o g 2 1 + 0 × l o g 2 0 ) = 0 H(X_1) = -(1\times{log}_2{1} + 0\times{log}_2{0}) = 0 H(X1)=−(1×log21+0×log20)=0
X 2 X_2 X2 的信息熵: H ( X 2 ) = − ( 0.25 × l o g 2 0.25 + 0.75 × l o g 2 0.75 ) = 0.81 H(X_2) = - (0.25\times{log}_2{0.25} + 0.75\times{log}_2{0.75}) = 0.81 H(X2)=−(0.25×log20.25+0.75×log20.75)=0.81
划分后的信息熵:
H A ( X ) = 200 + 0 200 + 0 + 200 + 600 × 0 + 200 + 600 200 + 0 + 200 + 600 × 0.81 = 0.65 H_A(X) = \frac{200+0}{200+0+200+600} \times 0 + \frac{200+600}{200+0+200+600}\times 0.81 = 0.65 HA(X)=200+0+200+600200+0×0+200+0+200+600200+600×0.81=0.65
信息增益:
G a i n ( A ) = H ( X ) − H A ( X ) = 0.97 − 0.65 = 0.32 Gain(A) = H(X) - H_A(X) = 0.97 - 0.65 = 0.32 Gain(A)=H(X)−HA(X)=0.97−0.65=0.32
划分方式2: 以“收入<10000元”为根节点进行划分,如下图所示,划分后的信息熵为0.924,信息增益为0.046,计算过程如下:
初始信息熵: H ( X ) = − ( 0.4 × l o g 2 0.4 + 0.6 × l o g 2 0.6 ) = 0.97 H(X) = - (0.4\times{log}_2{0.4}+0.6\times{log}_2{0.6}) = 0.97 H(X)=−(0.4×log20.4+0.6×log20.6)=0.97
X 1 X_1 X1 的信息熵: H ( X 1 ) = − ( 0.25 × l o g 2 0.25 + 0.75 × l o g 2 0.75 ) = 0.81 H(X_1) = -(0.25\times{log}_2{0.25} + 0.75\times{log}_2{0.75}) = 0.81 H(X1)=−(0.25×log20.25+0.75×log20.75)=0.81
X 2 X_2 X2 的信息熵: H ( X 2 ) = − ( 0.5 × l o g 2 0.5 + 0.5 × l o g 2 0.5 ) = 1 H(X_2) = - (0.5\times{log}_2{0.5} + 0.5\times{log}_2{0.5}) = 1 H(X2)=−(0.5×log20.5+0.5×log20.5)=1
划分后的信息熵:
H A ( X ) = 100 + 300 100 + 300 + 300 + 300 × 0 + 300 + 300 100 + 300 + 300 + 300 × 0.81 = 0.924 H_A(X) = \frac{100+300}{100+300+300+300} \times 0 + \frac{300+300}{100+300+300+300}\times 0.81 = 0.924 HA(X)=100+300+300+300100+300×0+100+300+300+300300+300×0.81=0.924
信息增益:
G a i n ( B ) = H ( X ) − H B ( X ) = 0.97 − 0.924 = 0.046 Gain(B) = H(X) - H_B(X) = 0.97 - 0.924 = 0.046 Gain(B)=H(X)−HB(X)=0.97−0.924=0.046
注意,信息增益在分类特别稀疏的时候无法呈现良好的效果,因此通常会只用信息增益率来比较上肢,称之为C4.5,即KaTeX parse error: Undefined control sequence: \自 at position 12: \frac{信息增益}\̲自̲身信息熵值
根据方式1划分后的信息增益为0.32,大于根据方式2划分后的信息增益0.046,因此选择根据方式1进行决策树的划分,这样能更好地降低系统的混乱程度。这个结论和之前用基尼系数计算得到的结论是一样的。
基尼系数涉及平方运算,而信息熵涉及相对复杂的对数函数运算,因此,目前决策树模型默认使用基尼系数作为建树依据,运算速度会较快。
商业实战中的数据量通常很大,不同情况下的基尼系数或信息熵的计算是人力难以完成的,因此需要利用机器不停地训练来找到最佳的分裂节点。在Python中,可以用Scikit-Learn库来快速建立一个决策树模型。
2.3.3 决策树剪枝策略
-
为什么要剪枝:决策树过拟合风险很大,理论上可以完全分得开数据[即层次加深,知道每个叶子节点都为一个数据]
-
剪枝策略:预剪枝,后剪枝
-
预剪枝:边建立决策树边进行剪枝的操作(更实用)
- 限制深度,叶子节点个数叶子节点样本数,信息增益量等
-
后剪枝:当建立完决策树后来进行剪枝操作
-
通过一定的衡量标准
C α ( T ) = C ( T ) + α ∣ T l e a f ∣ C_{\alpha}(T)=C(T)+\alpha|T_{leaf}| Cα(T)=C(T)+α∣Tleaf∣,其中 ∣ T l e a f ∣ |T_{leaf}| ∣Tleaf∣为此节点叶子节点个数,C(T)为此节点或者分裂的叶子节点的基尼系数, α \alpha α为系数,为自己指定数值, α \alpha α指定越大,则说明希望决策树越不过拟合
可以看到,叶子节点越多,损失就越大
-
决策树模型即能够解决分类问题,也能够解决回归问题【带标签的监督学习】
分类问题:根据叶子节点中的所有节点分类的众数决定其是哪个类别
回归问题:根据叶子节点的中的所有节点之间的方差决定划分好坏的标准,最终回归预测的时候,这个叶子节点的预测值就是所有节点的平均数
2.4 朴素贝叶斯模型
2.4.1 朴素贝叶斯的算法原理
贝叶斯分类是机器学习中应用极为广泛的分类算法之一,其产生自英国数学家贝叶斯对于逆概问题的思考。朴素贝叶斯是贝叶斯模型当中最简单的一种,其算法核心为如下所示的贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
其中P(A)为事件A发生的概率,P(B)为事件B发生的概率,P(A|B)表示在事件B发生的条件下事件A发生的概率,同理P(B|A)则表示在事件A发生的条件下事件B发生的概率。
举一个简单的例子:已知冬季一个人感冒(事件A)的概率P(A)为40%,一个人打喷嚏(事件B)的概率P(B)为80%,一个人感冒时打喷嚏的概率P(B|A)为100%,那么如果一个人开始打喷嚏,他感冒的概率P(A|B)为多少?
求解过程如下:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) = 100 % × 40 % 80 % = 50 % P(A|B) = \frac{P(B|A)P(A)}{P(B)}=\frac{100\%\times40\%}{80\%}=50\% P(A∣B)=P(B)P(B∣A)P(A)=80%100%×40%=50%
2.4.2 一维特征变量下的贝叶斯模型
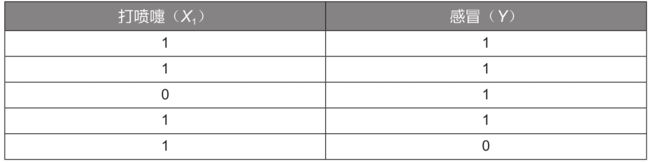
下面通过一个详细的例子来讲解贝叶斯模型的实战应用:如何判断一个人是否感冒。假设已经有5组样本数据,见下表:
为方便演示,这里只选取了一个特征变量“打喷嚏 ( X 1 ) (X_1) (X1) ”,其值为1表示打喷嚏,为0表示不打喷嚏;目标变量是“感冒(Y)”,其值为1表示感冒,为0表示未感冒。
现在要根据上述数据,利用贝叶斯公式预测一个人是否感冒。例如,一个人打喷嚏了 ( X 1 = 1 ) (X_1=1) (X1=1) ,那么他是否感冒了呢?这个问题实际上是要预测他感冒的概率 P ( Y ∣ X 1 ) P(Y|X_1) P(Y∣X1)。
将特征变量和目标变量代入贝叶斯公式,可获得如下所示的计算公式:
P ( Y ∣ X 1 ) = P ( X 1 ∣ Y ) P ( Y ) P ( X 1 ) P(Y|X_1) = \frac{P(X_1|Y)P(Y)}{P(X_1)} P(Y∣X1)=P(X1)P(X1∣Y)P(Y)
根据上述数据,可以计算在打喷嚏 ( X 1 = 1 ) (X_1=1) (X1=1) 的条件下,感冒(Y=1)的概率,计算过程如下:
P ( Y = 1 ∣ X 1 = 1 ) = P ( X 1 ∣ Y = 1 ) P ( Y = 1 ) P ( X 1 ) = 3 4 × 4 5 4 5 = 3 4 P(Y=1|X_1=1)=\frac{P(X_1|Y=1)P(Y=1)}{P(X_1)}=\frac{\frac{3}{4}\times\frac{4}{5}}{\frac{4}{5}}=\frac{3}{4} P(Y=1∣X1=1)=P(X1)P(X1∣Y=1)P(Y=1)=5443×54=43
其中 P ( X 1 = 1 ∣ Y = 1 ) P(X_1=1|Y=1) P(X1=1∣Y=1) 为在感冒的条件下打喷嚏的概率,这里感冒的4个样本中有3个样本打喷嚏,所以该概率为3/4;P(Y=1)为所有样本中感冒的概率,这里5个样本中有4个样本感冒,所以该概率为4/5; P ( X 1 = 1 ) P(X_1=1) P(X1=1) 为所有样本中打喷嚏的概率,这里5个样本中有4个样本打喷嚏,所以该概率为4/5。
同理,在打喷嚏 ( X 1 = 1 ) (X_1=1) (X1=1) 的条件下,未感冒(Y=0)的概率的计算过程如下:
P ( Y = 0 ∣ X 1 = 1 ) = P ( X 1 ∣ Y = 0 ) P ( Y = 0 ) P ( X 1 ) = 1 × 1 5 4 5 = 1 4 P(Y=0|X_1=1)=\frac{P(X_1|Y=0)P(Y=0)}{P(X_1)}=\frac{1\times\frac{1}{5}}{\frac{4}{5}}=\frac{1}{4} P(Y=0∣X1=1)=P(X1)P(X1∣Y=0)P(Y=0)=541×51=41
其中P ( X 1 = 1 ∣ Y = 0 ) (X_1=1|Y=0) (X1=1∣Y=0) 为在未感冒的条件下打喷嚏的概率,为1; P ( Y = 0 ) P(Y=0) P(Y=0) 为所有样本中未感冒的概率,为1/5; P ( X 1 = 1 ) P(X_1=1) P(X1=1) 为所有样本中打喷嚏的概率,为4/5。
因为3/4大于1/4,所以在打喷嚏的条件下感冒的概率要高于未感冒的概率。
2.4.3 二维特征变量下的贝叶斯模型
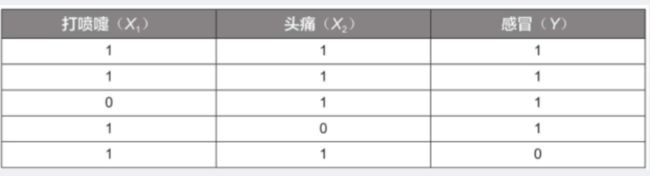
现在加入另一个特征变量——头痛 ( X 2 ) (X_2) (X2) ,其值为1表示头痛,为0表示不头痛;目标变量仍为感冒(Y)。
样本数据见下表:
根据上述数据,我们仍利用贝叶斯公式来预测一个人是否感冒。例如,一个人打喷嚏且头痛 ( X 1 = 1 , X 2 = 1 ) (X_1=1,X_2=1) (X1=1,X2=1) ,那么他是否感冒了呢?这个问题实际上是要预测他感冒的概率 P ( Y ∣ X 1 , X 2 ) P(Y|X_1,X_2) P(Y∣X1,X2) 。
将特征变量和目标变量代入贝叶斯公式,可获得如下所示的计算公式:
P ( Y ∣ X 1 , X 2 ) = P ( X 1 , X 2 ∣ Y ) P ( Y ) P ( X 1 , X 2 ) P(Y|X_1,X_2)=\frac{P(X_1, X_2|Y)P(Y)}{P(X_1,X_2)} P(Y∣X1,X2)=P(X1,X2)P(X1,X2∣Y)P(Y)
现在要计算并比较 P ( Y = 1 ∣ X 1 , X 2 ) P(Y=1|X_1,X_2) P(Y=1∣X1,X2) 与 P ( Y = 0 ∣ X 1 , X 2 ) P(Y=0|X_1,X_2) P(Y=0∣X1,X2) 的大小,由上述公式可知,两者的分母 P ( X 1 , X 2 ) P(X_1,X_2) P(X1,X2) 是相同的,所以直接计算并比较两者的分子 P ( X 1 , X 2 ∣ Y ) P ( Y ) P(X_1,X_2|Y)P(Y) P(X1,X2∣Y)P(Y) 的大小即可。
在计算之前,需要先引入朴素贝叶斯模型的独立性假设:朴素贝叶斯模型中的各个特征之间相互独立,即 P ( X 1 , X 2 ∣ Y ) = P ( X 1 ∣ Y ) P ( X 2 ∣ Y ) P(X_1,X_2|Y)=P(X_1|Y)P(X_2|Y) P(X1,X2∣Y)=P(X1∣Y)P(X2∣Y) 。因此,分子的计算公式可以转换为如下形式:
P ( X 1 , X 2 ∣ Y ) P ( Y ) = P ( X 1 ∣ Y ) P ( X 2 ∣ Y ) P ( Y ) P(X_1,X_2|Y)P(Y)=P(X_1|Y)P(X_2|Y)P(Y) P(X1,X2∣Y)P(Y)=P(X1∣Y)P(X2∣Y)P(Y)
在独立性假设的前提下,计算打喷嚏且头痛 ( X 1 = 1 , X 2 = 1 ) (X_1=1,X_2=1) (X1=1,X2=1) 的条件下感冒 ( Y = 1 ) (Y=1) (Y=1) 的概率 P ( Y = 1 ∣ X 1 = 1 , X 2 = 1 ) P(Y=1|X_1=1,X_2=1) P(Y=1∣X1=1,X2=1) ,就转化为计算 P ( X 1 = 1 ∣ Y = 1 ) P ( X 2 = 1 ∣ Y = 1 ) P ( Y = 1 ) P(X_1=1|Y=1)P(X_2=1|Y=1)P(Y=1) P(X1=1∣Y=1)P(X2=1∣Y=1)P(Y=1) 的值,计算过程如下:
P ( X 1 = 1 ∣ Y ) P ( X 2 = 1 ∣ Y = 1 ) P ( Y = 1 ) = 3 4 × 3 4 × 4 5 = 9 20 P(X_1=1|Y)P(X_2=1|Y=1)P(Y=1)=\frac{3}{4}\times\frac{3}{4}\times\frac{4}{5}=\frac{9}{20} P(X1=1∣Y)P(X2=1∣Y=1)P(Y=1)=43×43×54=209
同理,计算打喷嚏且头痛 ( X 1 = 1 , X 2 = 1 ) (X_1=1,X_2=1) (X1=1,X2=1) 的条件下未感冒 ( Y = 0 ) (Y=0) (Y=0) 的概率 P ( Y = 0 ∣ X 1 = 1 , X 2 = 1 ) P(Y=0|X_1=1,X_2=1) P(Y=0∣X1=1,X2=1) ,即转化为计算 P ( X 1 = 1 ∣ Y = 0 ) P ( X 2 = 1 ∣ Y = 0 ) P ( Y = 0 ) P(X_1=1|Y=0)P(X_2=1|Y=0)P(Y=0) P(X1=1∣Y=0)P(X2=1∣Y=0)P(Y=0) 的值,计算过程如下:
P ( X 1 = 1 ∣ Y = 0 ) P ( X 2 = 1 ∣ Y = 0 ) P ( Y = 0 ) = 1 × 1 × 1 5 = 1 5 P(X_1=1|Y=0)P(X_2=1|Y=0)P(Y=0)=1\times1\times\frac{1}{5}=\frac{1}{5} P(X1=1∣Y=0)P(X2=1∣Y=0)P(Y=0)=1×1×51=51
因为9/20大于1/5,所以在打喷嚏且头痛的条件下感冒的概率要高于未感冒的概率。
2.4.4 N维特征变量下的贝叶斯模型
我们可以在2个特征变量的基础上将贝叶斯公式推广至n个特征变量 X 1 , X 2 , … , X n X_1,X_2,…,X_n X1,X2,…,Xn,公式如下:
P ( X 1 , X 2 , . . . , X n ∣ Y ) P ( Y ) = P ( X 1 ∣ Y ) P ( X 2 ∣ Y ) P ( X 3 ∣ Y ) . . . P ( X n ∣ Y ) P ( Y ) P(X_1,X_2,...,X_n|Y)P(Y) = P(X_1|Y)P(X_2|Y)P(X_3|Y)...P(X_n|Y)P(Y) P(X1,X2,...,Xn∣Y)P(Y)=P(X1∣Y)P(X2∣Y)P(X3∣Y)...P(Xn∣Y)P(Y)
其中 P ( X 1 ∣ Y ) 、 P ( X 2 ∣ Y ) 、 P ( Y ) P(X_1|Y)、P(X_2|Y)、P(Y) P(X1∣Y)、P(X2∣Y)、P(Y)等数据都是已知的,由此可以计算在n个特征变量取不同的值的条件下,目标变量取某个值的概率,并且选择概率更高者对样本进行分类。
2.5 K近邻(KNN算法)
K近邻算法,简称KNN算法,是非常经典的机器学习算法。
2.5.1 K近邻算法的基本原理
K近邻算法就是在已有数据中寻找与它最相似的K个数据,或者说“离它最近”的K个数据。如果这K个数据多数属于某个类别,则该样本也属于这个类别。
以下图为例,假设五角星代表爱情片,三角形代表科幻片。此时加入一个新样本正方形,需要判断其类别。当选择以离新样本最近的3个近邻点(K=3)为判断依据时,这3个点由1个五角星和2个三角形组成,根据“少数服从多数”原则,可以认为新样本属于三角形的类别,即新样本是一部科幻片。同理,当选择离新样本最近的5个近邻点(K=5)为判断依据时,这5个点由3个五角星和2个三角形组成,根据“少数服从多数”原则,可以认为新样本属于五角星的类别,即新样本是一部爱情片。
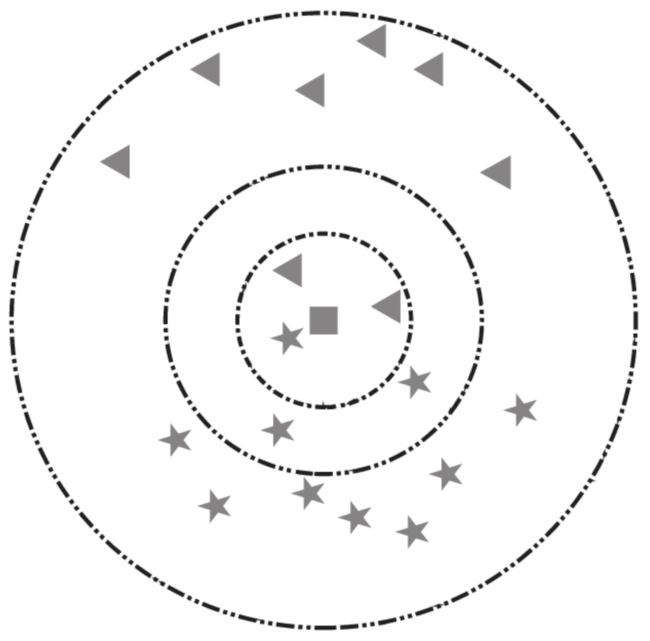
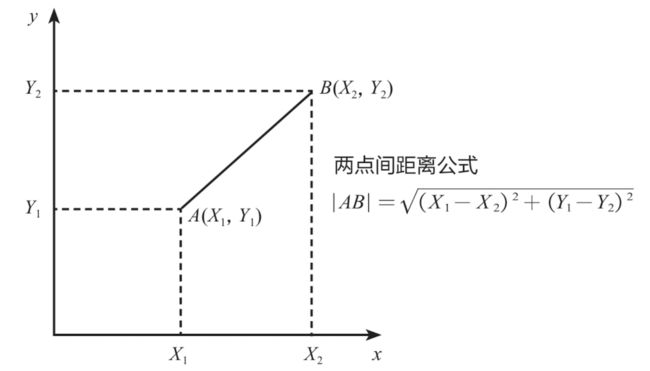
明白了K的含义后,下面来学习如何判断2个数据的相似度,或者说2个数据的距离。这里采用最为常见的欧氏距离来定义向量空间内2个点的距离,对于二维空间而言,样本A的2个特征值为 ( X 1 , Y 1 ) (X_1, Y_1) (X1,Y1) ,样本B的2个特征值为 ( X 2 , Y 2 ) (X_2, Y_2) (X2,Y2) ,那么2个样本的距离计算公式如下:
∣ A B ∣ = ( X 1 − X 2 ) 2 + ( Y 1 − Y 2 ) 2 |AB| = \sqrt[]{(X_1-X_2)^2+(Y_1-Y_2)^2} ∣AB∣=(X1−X2)2+(Y1−Y2)2
这个其实就是常见的两点间距离公式,如下图所示,其适用于只有2个特征变量的情况。
实际应用中,数据的特征通常有n个,此时可将该距离公式推广到n维空间,如n维向量空间内A点坐标为 ( X 1 , X 2 , X 3 , . . . , X n ) (X_1,X_2,X_3,...,X_n) (X1,X2,X3,...,Xn) ,B点坐标为 ( Y 1 , Y 2 , Y 3 , . . . , Y n ) (Y_1,Y_2,Y_3,...,Y_n) (Y1,Y2,Y3,...,Yn) ,那么A、B两点间的欧氏距离计算公式如下:
∣ A B ∣ = ( X 1 − Y 1 ) 2 + ( X 2 − Y 2 ) 2 + ( X 3 − Y 3 ) 2 + . . . + ( X n − Y n ) 2 |AB| = \sqrt[]{(X_1-Y_1)^2+(X_2-Y_2)^2+(X_3-Y_3)^2+...+(X_n-Y_n)^2} ∣AB∣=(X1−Y1)2+(X2−Y2)2+(X3−Y3)2+...+(Xn−Yn)2
2.5.2 K近邻算法的计算步骤
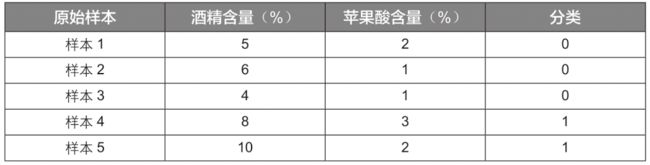
这里通过一个简单的例子“如何判断葡萄酒的种类”来讲解K近邻算法的计算步骤。商业实战中用于评判葡萄酒的指标有很多,为方便演示,这里只根据“酒精含量”和“苹果酸含量”2个特征变量将葡萄酒分为2类,并且原始样本数据只有5组,见下表:
其中“酒精含量”代表葡萄酒中酒精的含量,“苹果酸含量”代表葡萄酒中苹果酸的含量,“分类”取值为0代表葡萄酒A,取值为1代表葡萄酒B。
现在需要使用K近邻算法对一个新样本进行分类,该新样本的特征数据见下表,那么这个新样本是属于葡萄酒A还是葡萄酒B呢?
此时可以利用距离公式来计算新样本与已有样本之间的距离,即不同样本间的相似度。例如,新样本与样本1的距离计算公式如下:
∣ A B ∣ = ( 5 − 7 ) 2 + ( 2 − 1 ) 2 = 2.24 |AB| = \sqrt[]{(5-7)^2+(2-1)^2} = 2.24 ∣AB∣=(5−7)2+(2−1)2=2.24
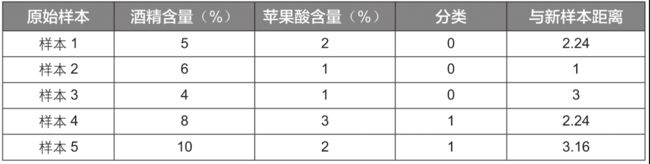
同理可以计算新样本与其他原始样本的距离,结果如下:
计算出各个原始样本与新样本的距离后,再根据距离由近及远排序,结果如下:
如果令K值等于1,也就是以离新样本最近的原始样本的种类作为新样本的种类,此时新样本离样本2最近,则新样本的分类为0,也就是葡萄酒A。
如果令K值等于3,也就是以离新样本最近的3个原始样本的多数样本的种类为判断依据,此时最近的3个原始样本是样本2、样本1、样本4,它们中以分类0居多,所以判定新样本的分类为0,也就是葡萄酒A。
2.5.3 k值的选取
-
选取较小的k值,那么就会意味着我们的整体模型会变得复杂,容易发生过拟合!
假设我们选取k=1这个极端情况,怎么就使得模型变得复杂,假设我们有训练数据和待分类点如下图:
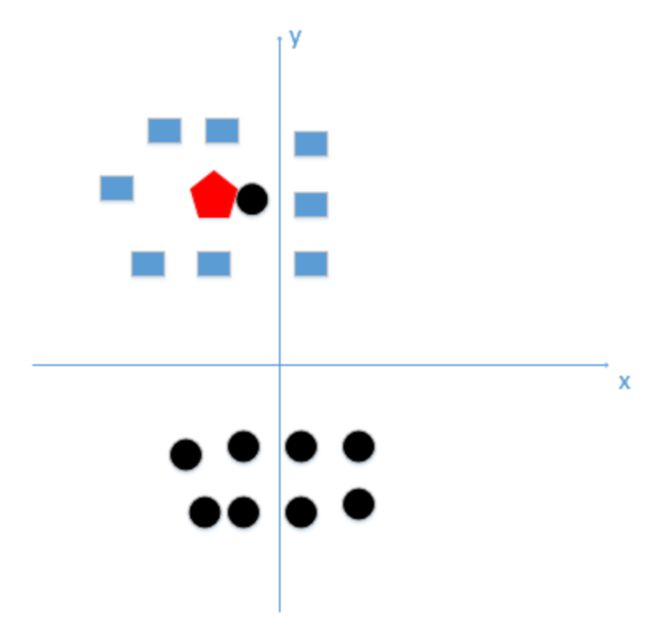
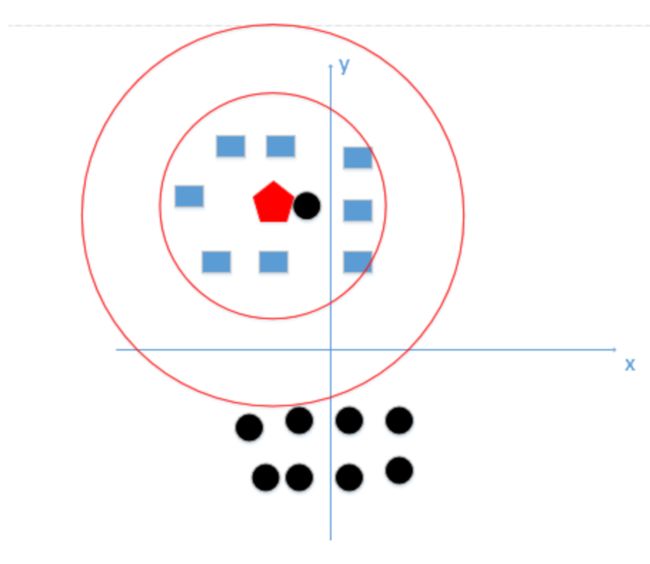
上图中有俩类,一个是黑色的圆点,一个是蓝色的长方形,现在待分类点是红色的五边形。
由图中可以得到,很容易我们能够看出来五边形离黑色的圆点最近,且k等于1最终判定待分类点是黑色的圆点。
由这个处理过程可以看出问题:如果k太小了,比如等于1,那么模型就太复杂了,我们很容易学习到噪声,也就非常容易判定为噪声类别。
所谓的过拟合就是在训练集上准确率非常高,而在测试集上准确率低,经过上例,我们可以得到k太小会导致过拟合,很容易将一些噪声(如上图离五边形很近的黑色圆点)学习到模型中,而忽略了数据真实的分布!
-
k的取值过大意味着模型变得简单
假设K=N(N为训练样本的个数),那么无论输入的实例是什么,都是简单地将预测它属于在训练实例中最多的类,相当于只是拿数据统计了一下各个数据的类别,找出最大的。如下图所示:
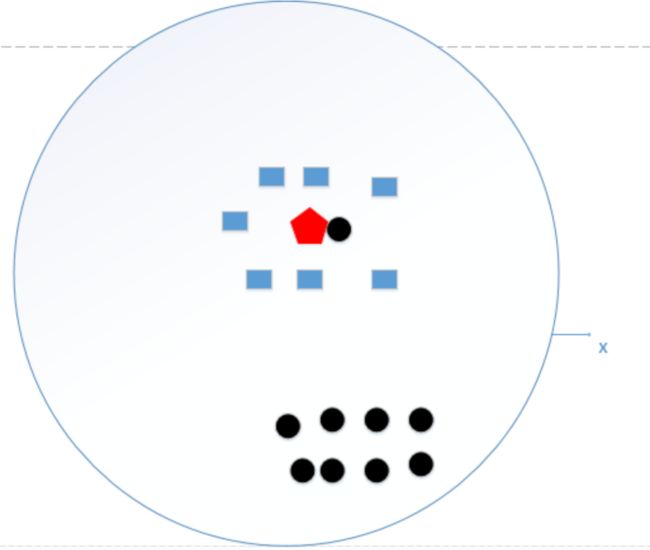
统计了黑色圆形是8个,长方形个数是7个,若k=N,得出结论:红色五边形是属于黑色圆形的(明显错误)
-
k值既不能过大也不能过下,上述例子k值最好在红色边界的范围内:
-
如何选取k值呢?
一般选取一个较小的数值,通常采取 交叉验证法来选取最优的k值。(也就是说,选取k值很重要的关键是实验调参,类似于神经网络选取多少层这种,通过调整超参数来得到一个较好的结果)
2.5.4 数据标准化
上述演示数据中,不同特征变量的量纲级别相差不大,如果把“酒精含量”数据都放大为原来的10倍,“苹果酸含量”数据保持不变,那么两者的量纲级别就相差较大了,见下表:
此时如果直接使用K近邻算法来搭建模型,那么“酒精含量”在模型中的重要性将远远超过“苹果酸含量”的重要性,这样会丧失“苹果酸含量”这一特征变量的作用,而且结果也会有较大误差。举例来说,对于一个新样本,其“酒精含量”为70%,“苹果酸含量”为1%,此时它与样本1的距离计算如下:
∣ A B ∣ = ( 50 − 70 ) 2 + ( 2 − 1 ) 2 = 20.02 |AB| = \sqrt[]{(50-70)^2+(2-1)^2} = 20.02 ∣AB∣=(50−70)2+(2−1)2=20.02
可以看到,此时的距离几乎就是由“酒精含量”主导,“苹果酸含量”由于量纲级别相差较大,几乎不发挥作用,如果不进行数据预处理,会导致预测结果有失偏颇。
因此,如果不同特征变量的量纲级别相差较大且在建模时相互影响,我们通常会对数据进行预处理,该手段称为数据标准化或数据归一化。数据标准化的常见方法有min-max标准化(也称离差标准化)和Z-score标准化(也称均值归一化)。
-
最值归一化(normalization): 把所有数据映射到0-1之间。
最值归一化的使用范围是特征的分布具有明显边界的(分数0~100分、灰度0~255),受outlier的影响比较大x s c a l e = x − x m i n x m a x − x m i n x_{scale} = \frac {x - x_{min}} {x_{max} - x_{min}} xscale=xmax−xminx−xmin
-
均值方差归一化(standardization): 把所有数据归一到均值为0方差为1的分布中。
适用于数据中没有明显的边界,有可能存在极端数据值的情况.x s c a l e = x − x m e a n S x_{scale} = \frac {x - x_{mean}} {S} xscale=Sx−xmean
2.6 支持向量机(SVM)
2.6.1 初识SVM
SVM的英文全称叫Support Vector Machine,中文名为支持向量机。在机器学习领域,SVM是一种常见的分类方法,属于有监督的学习模型。
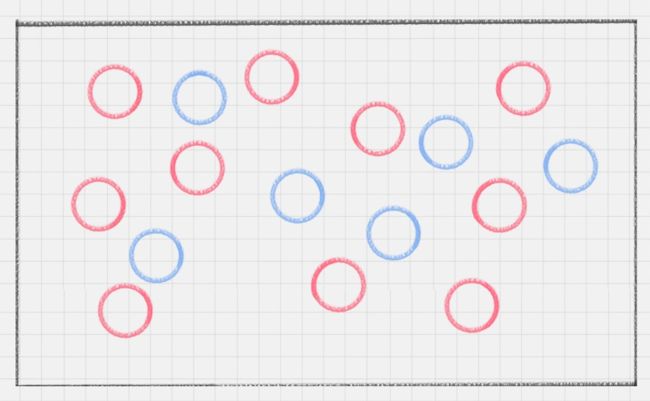
为了理解SVM模型,我们先来看一个小练习。
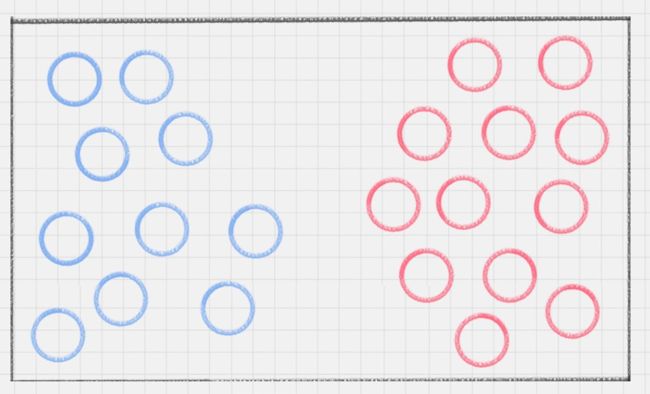
桌子上放了红、蓝两种颜色的球,我们如何用一条线将两种球分开?
这种情况很好解决,我们在两种颜色的球之间画条直线就好,如下图所示:
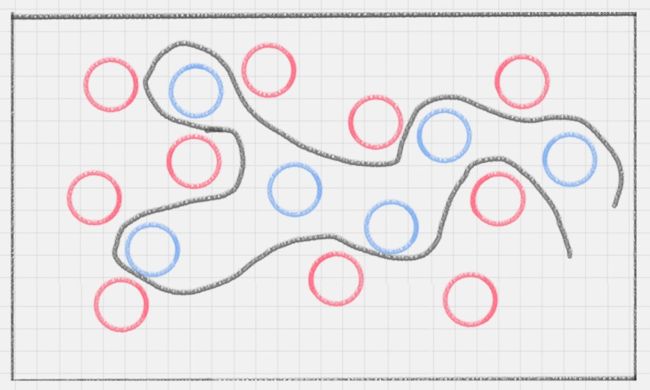
接下来难度升级,桌子上依然放两种颜色的球,但是摆放不再规律,如下图所示:
这时如何用一条线将两种球分开?首先想到的是用曲线,如下图所示:
直线变成了曲线,且曲线的复杂度很高。如果在同一个平面来看,红蓝两种颜色的球很难分开,那有没有一种方式,可以让它们自然地分开呢?
一个巧妙的办法就是,猛拍一下桌子,让小球腾空而起,在腾起的一刹那,恰好出现一个水平切面,把红蓝两种颜色的球分开,如下图所示:
这时,二维平面变成了三维空间。原来的曲线变成了一个平面。这个平面,叫做超平面。
2.6.2 SVM的工作原理
SVM的计算过程就是寻找超平面的过程。
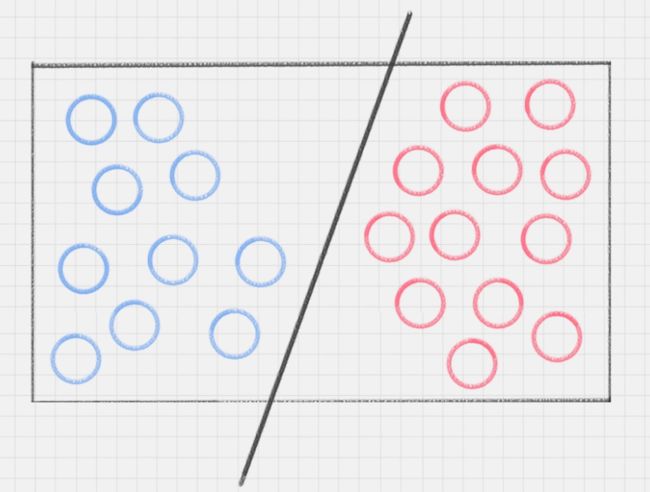
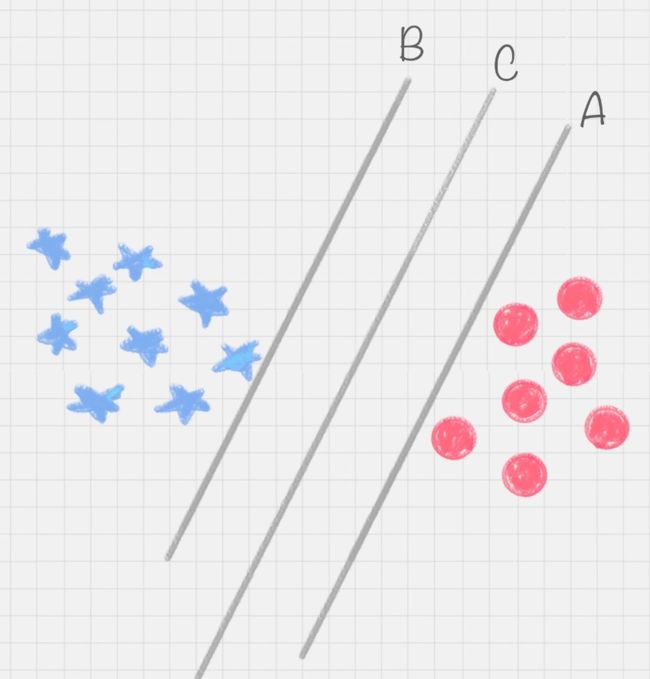
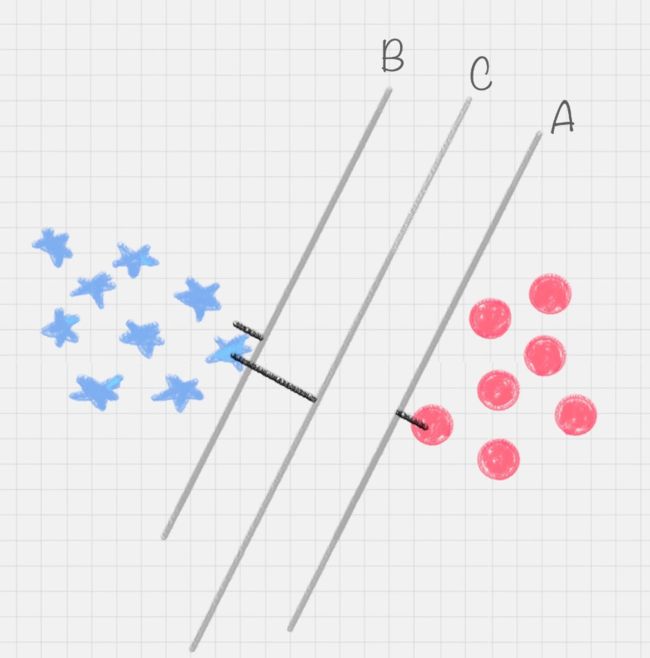
我们再来看上述小练习,其实我们可以划出多个直线,如下图所示:
图中的直线B更靠近蓝色球,在真实场景下,球如果再多一些的话,蓝色球可能就被划分到了直线B的右侧,被认为是红色球。同样直线A更靠近红色球,同理,红色球再多的话,也可能被误认为是蓝色球。所以相比于直线A和直线B,直线C的划分更优。因为它的健壮性更强。
那怎样才能找到最优解呢?我们需要引入一个新的概念分类间隔。
实际上,我们的分类环境不是在二维平面中的,而是在多维空间中,这样直线 C 就变成了决策面 C。
在保证决策面不变,且分类不产生错误的情况下,我们可以移动决策面C,直到产生两个极限的位置:如图中的决策面 A 和决策面 B。极限的位置是指,如果越过了这个位置,就会产生分类错误。这样的话,两个极限位置 A 和 B 之间的分界线 C 就是最优决策面。极限位置到最优决策面 C 之间的距离,就是“分类间隔”,英文叫做 margin。
如果我们转动这个最优决策面,会发现可能存在多个最优决策面,它们都能把数据集正确分开,这些最优决策面的分类间隔可能是不同的,而那个拥有“最大间隔”(max margin)的决策面就是 SVM 要找的最优解。
在上面这个例子中,如果我们把红蓝两种颜色的球放到一个三维空间里,会发现决策面就变成了一个平面。可以用线性函数来表示,如果在一维空间里就表示一个点,在二维空间里表示一条直线,在三维空间中代表一个平面,当然空间维数还可以更多,这样我们给这个线性函数起个名称叫做“超平面”。超平面的数学表达可以写成:
g ( x ) = w T x + b ( w , x ∈ R n ) g(x) = w^Tx+b \quad (w,x \in R^n) g(x)=wTx+b(w,x∈Rn)
在公式里,w、x 是n维空间里的向量,其中x是函数变量;w是法向量(特征系数的向量)。法向量这里指的是垂直于平面的直线所表示的向量,它决定了超平面的方向。
SVM 就是帮我们找到一个超平面,这个超平面能将不同的样本划分开,同时使得样本集中的点到这个分类超平面的最小距离(即分类间隔)最大化。
在这个过程中,支持向量就是离分类超平面最近的样本点,如果确定了支持向量也就确定了这个超平面。所以支持向量决定了分类间隔到底是多少,而在最大间隔以外的样本点,其实对分类都没有意义。所以说, SVM就是求解最大分类间隔的过程,我们还需要对分类间隔的大小进行定义。
首先,我们定义某类样本集到超平面的距离是这个样本集合内的样本到超平面的最短距离。用 d i d_i di 代表点 x i x_i xi 到超平面 w x i + b = 0 wx_i+b=0 wxi+b=0 的欧氏距离。因此我们要求 d i d_i di 的最大值,用它来代表这个样本到超平面的最短距离。 d i d_i di 可以用公式计算得出:
d i = ∣ w x i + b ∣ ∣ ∣ w ∣ ∣ d_i = \frac{|wx_i+b|}{||w||} di=∣∣w∣∣∣wxi+b∣
其中||w||为超平面的范数, d i d_i di 的公式可以用解析几何知识【点到直线的距离】进行推导,这里不再解释。
我们的目标就是找出所有分类间隔中最大的那个值对应的超平面。在数学上,这是一个凸优化问题(凸优化就是关于求凸集中的凸函数最小化的问题,这里不具体展开)。通过凸优化问题,最后可以求出最优的 w 和 b,也就是我们想要找的最优超平面。中间求解的过程会用到拉格朗日乘子,和 KKT(Karush-Kuhn-Tucker)条件。数学公式比较多,这里不进行展开。
详细推导可见:机器学习笔记十三之支撑向量机(SVM) | 程序员说 (devtalking.com)
2.6.3 硬间隔、软间隔和非线性SVM
假如数据是完全的线性可分的,那么学习到的模型可以称为硬间隔支持向量机。换个说法,硬间隔指的就是完全分类准确,不能存在分类错误的情况。软间隔,就是允许一定量的样本分类错误。
因为实际工作中的数据没有那么“干净”,或多或少都会存在一些噪点。所以线性可分是个理想情况。这时,我们需要使用到软间隔 SVM(近似线性可分),比如下面这种情况:
注意:软间隔称之为soft-margin
其建立新的目标函数: m i n 1 2 ∣ ∣ w ∣ ∣ + C ∑ i = 1 n ξ i min\frac{1}{2}||w||^+C\sum^n_{i=1}\xi_i min21∣∣w∣∣+C∑i=1nξi
当C趋近于很大时:意味着分类严格不能有错误
当C趋近于很小时:意味着可以有更大的错误容忍
高斯核函数:利用相似度来变换特征
对于样本中的每一个数据,利用其相似度特征来替换原来本身的特征;相似度特征就是当前样本点和其他样本点通过相似度函数计算出来的新的特征值
相似度函数为:
$\Phi\gamma(x,l)=exp(-\gamma||x-l||^2) $
SVM中利用了核函数的计算技巧,大大降低了计算的复杂度:
- 增加 γ \gamma γ使高斯曲线变窄,因此每个实例的影响范围都较小;决策边界最终变得更加不规则,在个别实例周围摆动。因此过拟合的风险增加
- 减少 γ \gamma γ使高斯曲线变宽,因此每个实例具有更大的影响范围,并且决策边界更加平滑。因此过拟合的风险减少
另外还存在一种情况,就是非线性支持向量机。
比如下面的样本集就是个非线性的数据。图中的两类数据,分别分布为两个圆圈的形状。那么这种情况下,不论是多高级的分类器,只要映射函数是线性的,就没法处理SVM也处理不了。这时,我们需要引入一个新的概念:核函数。它可以将样本从原始空间映射到一个更高维的特质空间中,使得样本在新的空间中线性可分。这样我们就可以使用原来的推导来进行计算,只是所有的推导是在新的空间,而不是在原来的空间中进行。
所以在非线性 SVM 中,核函数的选择就是影响SVM最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid核,或者是这些核函数的组合。这些函数的区别在于映射方式的不同。通过这些核函数,我们就可以把样本空间投射到新的高维空间中【高维空间的点是由低维空间的点通过和函数做内积得到】。
当然软间隔和核函数的提出,都是为了方便我们对上面超平面公式中的w*和b*进行求解,从而得到最大分类间隔的超平面。
2.6.4 用SVM如何解决多分类问题
SVM本身是一个二值分类器,最初是为二分类问题设计的,也就是回答Yes或者是No。而实际上我们要解决的问题,可能是多分类的情况,比如对文本进行分类,或者对图像进行识别。
针对这种情况,我们可以将多个二分类器组合起来形成一个多分类器,常见的方法有“一对多法”和“一对一法”两种。
(1) 一对多法
假设我们要把物体分成A、B、C、D四种分类,那么我们可以先把其中的一类作为分类1,其他类统一归为分类2。这样我们可以构造4种SVM,分别为以下的情况:
(1)样本A作为正集,B,C,D 作为负集;
(2)样本B作为正集,A,C,D 作为负集;
(3)样本C作为正集,A,B,D 作为负集;
(4)样本D作为正集,A,B,C 作为负集。
这种方法,针对K个分类,需要训练K个分类器,分类速度较快,但训练速度较慢,因为每个分类器都需要对全部样本进行训练,而且负样本数量远大于正样本数量,会造成样本不对称的情况,而且当增加新的分类,比如第K+1类时,需要重新对分类器进行构造。
(2) 一对一法
一对一法的初衷是想在训练的时候更加灵活。我们可以在任意两类样本之间构造一个SVM,这样针对K类的样本,就会有C(k,2)类分类器。
比如我们想要划分A、B、C三个类,可以构造 3 个分类器:
(1)分类器 1:A、B;
(2)分类器 2:A、C;
(3)分类器 3:B、C。
当对一个未知样本进行分类时,每一个分类器都会有一个分类结果,即为1票,最终得票最多的类别就是整个未知样本的类别。
这样做的好处是,如果新增一类,不需要重新训练所有的SVM,只需要训练和新增这一类样本的分类器。而且这种方式在训练单个SVM模型的时候,训练速度快。
但这种方法的不足在于,分类器的个数与K的平方成正比,所以当K较大时,训练和测试的时间会比较慢。
2.6.5 总结
SVM分类器在解决二分类问题时性能卓越。针对多分类的情况,可以用一对多或一对一的方法,把多个二分类器组合成一个多分类器。
另外,对于SVM分类器,我们需要掌握以下三个内容:
(1)完全线性可分情况下的线性分类器,也就是线性可分的情况,是最原始的SVM,它最核心的思想就是找到最大的分类间隔;
(2)大部分线性可分情况下的线性分类器,引入了软间隔的概念。软间隔,就是允许一定量的样本分类错误;
(3)线性不可分情况下的非线性分类器,引入了核函数。它让原有的样本空间通过核函数投射到了一个高维的空间中,从而变得线性可分。
2.6.6 优缺点
优点
- 有严格的数学理论支持,可解释性强,不依靠统计方法,从而简化了通常的分类和回归问题;
- 能找出对任务至关重要的关键样本(即:支持向量);
- 采用核技巧之后,可以处理非线性分类/回归任务;
- 最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
缺点
- 训练时间长。当采用 SMO 算法时,由于每次都需要挑选一对参数,因此时间复杂度为 O ( N 2 ) O(N^2) O(N2) ,其中 N 为训练样本的数量;
- 当采用核技巧时,如果需要存储核矩阵,则空间复杂度为 O ( N 2 ) O(N^2) O(N2)$ ;
- 模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂度较高。
因此支持向量机目前只适合小批量样本的任务,无法适应百万甚至上亿样本的任务。
详细内容见:【机器学习】支持向量机 SVM(非常详细) - 知乎 (zhihu.com)
2.7 K-means算法
基本概念:
- 要得到簇的个数,需要指定k值
- 质心:均值,即向量各维度取平均即可
- 距离的度量:常用欧几里得距离和余弦相似度(先标准化)
- 优化目标: m i n ∑ i = 1 k ∑ x ∈ C i d i s t ( c i , x ) 2 min\sum^k_{i=1}\sum_{x\in C_i}dist(c_i,x)^2 min∑i=1k∑x∈Cidist(ci,x)2
网页版k-means可视化:Visualizing K-Means Clustering (naftaliharris.com)
K-Means算法是最常用的一种聚类算法,是无监督问题的典型代表(无标签)
算法名称中的K代表类别数量,Means代表每个类别内样本的均值,所以KMeans算法又称为K-均值算法。
KMeans算法以距离作为样本间相似度的度量标准,将距离相近的样本分配至同一个类别。样本间距离的计算方式可以是欧氏距离、曼哈顿距离、余弦相似度等,KMeans算法通常采用欧氏距离来度量各样本间的距离。
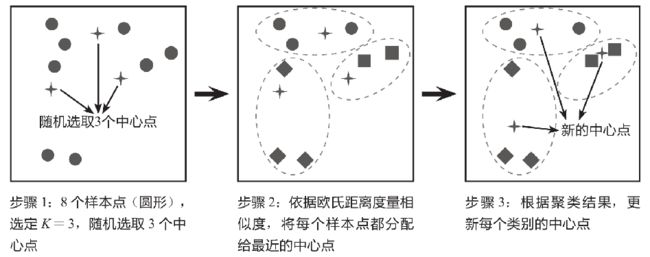
KMeans算法的核心思想是对每个样本点计算到各个质心(中心点)的距离,并将该样本点分配给距离最近的中心点代表的类别,一次迭代完成后,根据聚类结果更新每个类别的质心(中心点),然后重复之前操作再次迭代,直到前后两次分类结果没有差别(即某类的点不在因为质心的更新而归于其他类的点)。如下图所示的简单案例解释了KMeans算法的原理,该案例的目的是将8个样本点聚成3个类别(K=3)。
2.7.1 经典k-means算法描述
2.7.2 优缺点
优点
- 容易理解,聚类效果不错,虽然是局部最优, 但往往局部最优就够了;
- 处理大数据集的时候,该算法可以保证较好的伸缩性;
- 当簇近似高斯分布的时候,效果非常不错;
- 算法复杂度低。
缺点
- K 值需要人为设定,不同 K 值得到的结果不一样;
- 对初始的簇中心敏感,不同选取方式会得到不同结果;
- 对异常值敏感;
- 样本只能归为一类,不适合多分类任务;
- 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类(比如各种任意形状的簇,如环状的)。
2.7.3 K-means算法的调优与改进
针对 K-means 算法的缺点,我们可以有很多种调优方式:如数据预处理(去除异常点),合理选择 K 值,高维映射等。以下将简单介绍:
(1) 数据预处理
K-means 的本质是基于欧式距离的数据划分算法,均值和方差大的维度将对数据的聚类产生决定性影响。所以未做归一化处理和统一单位的数据是无法直接参与运算和比较的。常见的数据预处理方式有:数据归一化,数据标准化。
此外,离群点或者噪声数据会对均值产生较大的影响,导致中心偏移,因此我们还需要对数据进行异常点检测。
(2) 合理选择 K 值
K 值的选取对 K-means 影响很大,这也是 K-means 最大的缺点,常见的选取 K 值的方法有:手肘法、Gap statistic 方法。
手肘法:
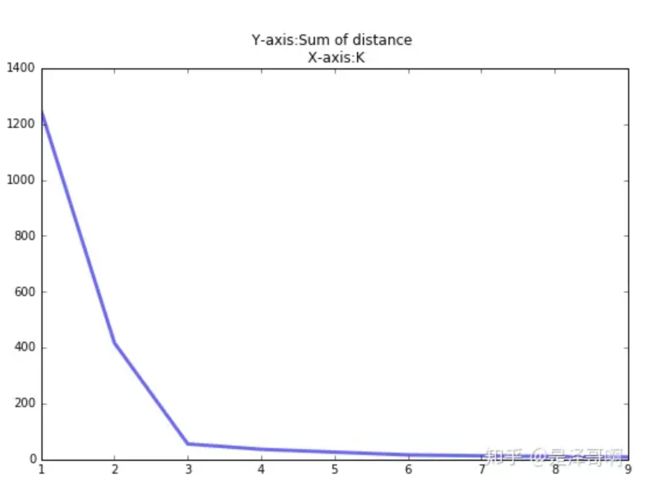
当 K < 3 时,曲线急速下降;当 K > 3 时,曲线趋于平稳,通过手肘法我们认为拐点 3 为 K 的最佳值。
手肘法需要人工看,不够自动化,因此推出Gap stastic方法,出自这个方法出自斯坦福大学的几个学者的论文:Estimating the number of clusters in a data set via the gap statistic
G a p ( k ) = E ( l o g D k ) − l o g D k Gap(k)=E(logD_k)-logD_k Gap(k)=E(logDk)−logDk
其中 D k D_k Dk 为损失函数,这里 E ( l o g D k ) E(logD_k) E(logDk)指的是 l o g D k logD_k logDk的期望。这个数值通常通过蒙特卡洛模拟产生,我们在样本里所在的区域中按照均匀分布随机产生和原始样本数一样多的随机样本,并对这个随机样本做 K-Means,从而得到一个 D k D_k Dk。如此往复多次,通常 20 次,我们可以得到 20 个 l o g D k logD_k logDk。对这 20 个数值求平均值,就得到了 E ( l o g D k ) E(logD_k) E(logDk)的近似值。最终可以计算 Gap Statisitc。而 Gap statistic 取得最大值所对应的 K 就是最佳的 K。

由图可见,当 K=3 时,Gap(K) 取值最大,所以最佳的簇数是 K=3。Github 上一个项目叫 gap_statistic ,可以更方便的获取建议的类簇个数。
2.7.4 三种改进算法
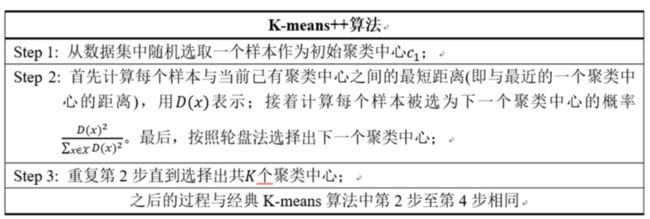
(1)k-means++
2007年由D. Arthur等人提出的K-means++针对图1中的第一步做了改进。可以直观地将这改进理解成这K个初始聚类中心相互之间应该分得越开越好。整个算法的描述如下所示:
-
下面结合一个简单的例子说明K-means++是如何选取初始聚类中心的。数据集中共有8个样本,分布以及对应序号如下图所示:

-
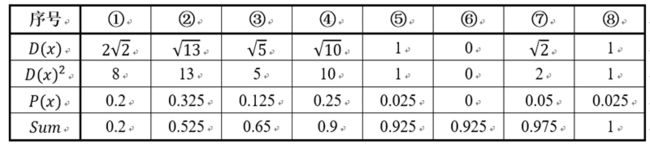
假设经过k-means++步骤一后6号点被选择为第一个初始聚类中心,那在进行步骤二时每个样本的***D(x)***和被选择为第二个聚类中心的概率如下表所示:
其中的P(x)就是是每个样本被选为下一个聚类中心的概率。最后一行*Sum是概率P(x)的累加和,用于轮盘法选择出第二个聚类中心。方法是随机产生出一个0~1之间的随机数,判断它属于哪个区间,那么该区间对应的序号就是被选择出来的第二个聚类中心了。例如1号点的区间为[0,0.2),2号点的区间为[0.2, 0.525)。
从上表可以直观的看到第二个初始聚类中心是1号,2号,3号,4号中的一个的概率为0.9。而这4个点正好是离第一个初始聚类中心6号点较远的四个点。这也验证了K-means的改进思想:即离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。可以看到,该例的K值取2是比较合适的。当K值大于2时,每个样本会有多个距离,需要取最小的那个距离作为D(x)。
(2) 采用核函数
基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布,但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化,这时算法又称为核 K-means 算法,是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射,将输入空间中的数据点映射到高位的特征空间中,并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
(3)ISODATA
如之前所述,K-means和K-means++的聚类中心数K是固定不变的。而ISODATA算法在运行过程中能够根据各个类别的实际情况进行两种操作来调整聚类中心数K:
(1)分裂操作,对应着增加聚类中心数;
(2)合并操作,对应着减少聚类中心数。
下面首先给出ISODATA算法的输入(输入的数据和迭代次数不再单独介绍):
[1] 预期的聚类中心数目Ko:虽然在ISODATA运行过程中聚类中心数目是可变的,但还是需要由用户指定一个参考标准。事实上,该算法的聚类中心数目变动范围也由Ko决定。具体地,最终输出的聚类中心数目范围是 [Ko/2, 2Ko]。
[2] 每个类所要求的最少样本数目Nmin:用于判断当某个类别所包含样本分散程度较大时是否可以进行分裂操作。如果分裂后会导致某个子类别所包含样本数目小于Nmin,就不会对该类别进行分裂操作。
[3] 最大方差Sigma:用于衡量某个类别中样本的分散程度。当样本的分散程度超过这个值时,则有可能进行分裂操作(注意同时需要满足**[2]**中所述的条件)。
[4] 两个类别对应聚类中心之间所允许最小距离dmin:如果两个类别靠得非常近(即这两个类别对应聚类中心之间的距离非常小),则需要对这两个类别进行合并操作。是否进行合并的阈值就是由dmin决定。
相信很多人看完上述输入的介绍后对ISODATA算法的流程已经有所猜测了。的确,ISODATA算法的原理非常直观,不过由于它和其他两个方法相比需要额外指定较多的参数,并且某些参数同样很难准确指定出一个较合理的值,因此ISODATA算法在实际过程中并没有K-means++受欢迎。
-
首先给出ISODATA算法主体部分的描述,如下图所示:
-
上面描述中没有说明清楚的是第5步中的分裂操作和第6步中的合并操作。下面首先介绍合并操作:
-
ISODATA算法中的分裂操作。
-
最后,针对ISODATA算法总结一下:该算法能够在聚类过程中根据各个类所包含样本的实际情况动态调整聚类中心的数目。如果某个类中样本分散程度较大(通过方差进行衡量)并且样本数量较大,则对其进行分裂操作;如果某两个类别靠得比较近(通过聚类中心的距离衡量),则对它们进行合并操作。
注:ISODATA-分裂操作的第1步和第2步。同样地以图三所示数据集为例,假设最初1,2,3,4,5,6,8号被分到了同一个类中,执行第1步和第2步结果如下所示:
而在正确分类情况下(即1,2,3,4为一类;5,6,7,8为一类),方差为0.33。因此,目前的方差远大于理想的方差,ISODATA算法就很有可能对其进行分裂操作。
2.7.5 DBSCAN算法
网页版可视化:https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/
基本概念
-
Density-Based Spatial Clustering of Applications with Noise(基于密度的噪声应用空间聚类)
-
核心对象:若某个点的密度达到算法设定的阈值则其为核心点。(即 r 邻域内点的数量不小于 minPts)
-
ϵ-邻域的距离阈值:设定的半径r
-
直接密度可达:若某点p在点q的 r 邻域内,且q是核心点则p-q直接密度可达。
-
密度可达:若有一个点的序列 q 0 、 q 1 、 … q k q_0、q_1、…q_k q0、q1、…qk,对任意 q i − q i − 1 q_i-q_{i-1} qi−qi−1是直接密度可达的,则称从 q 0 q_0 q0到 q k q_k qk密度可达,这实际上是直接密度可达的“传播”。
-
密度相连:若从某核心点p出发,点q和点k都是密度可达的,则称点q和点k是密度相连的。
-
边界点:属于某一个类的非核心点,不能发展下线了[就是这个以某个点为核心点的圈内已经无其他点]
-
噪声点:不属于任何一个类簇的点,从任何一个核心点出发都是密度不可达的
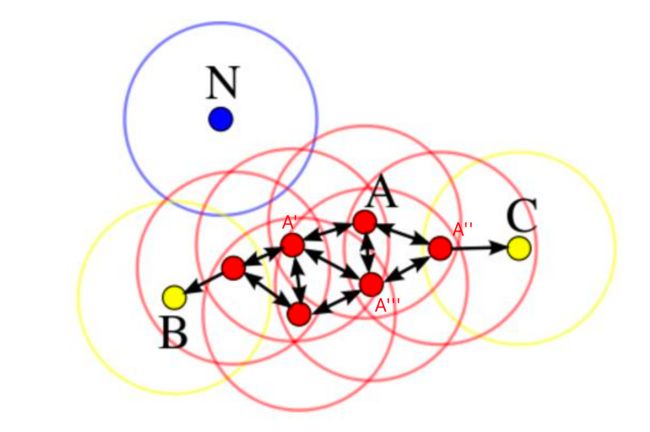
举例:
上述例子中:
A为核心对象,以A为核心有直接密度可达的点A’,A’‘,A’‘’
以这三个点为中心绘制半径为r的圆,得到B,C两点,但是BC两点为核心对象的圆中,只包含她的上线顶点,因此
B,C为边界点
没有任何一个点为核心对象的圆圈内能包含N点,因此
N点为离群点
工作流程
-
输入参数
- 参数D:输入数据集
- 参数ϵ:指定半径
- MinPts:密度阈值
-
算法框架

-
对于参数应该如何取值?
- 半径ϵ,可以根据K距离来设定:找突变)
- K距离:给定数据集P={p(i); i=0,1,…n},计算点P(i)到集合D的子集S中所有点之间的距离,距离按照从小到大的顺序排序,d(k)就被称为k-距离。(就是假设从小到大排序,突然一个点使得d(k)急速增大,并且后续保持这个趋势,则半径可以选择这个突变点前的距离作为密度)
- MinPts: k-距离中k的值,一般取的小一些,多次尝试
优缺点
-
优点
-
缺点
- 高维数据有些困难(可以做降维)
- Sklearn中效率很慢(数据削减策略)
- 参数难以选择(参数对结果的影响非常大
2.8 EM算法
EM 算法,全称 Expectation Maximization Algorithm。期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最大似然估计或极大后验概率估计。
本文思路大致如下:先简要介绍其思想,然后举两个例子帮助大家理解,有了感性的认识后再进行严格的数学公式推导。
2.8.1. 思想
EM 算法的核心思想非常简单,分为两步:Expection-Step 和 Maximization-Step。E-Step 主要通过观察数据和现有模型来估计参数,然后用这个估计的参数值来计算似然函数的期望值;而 M-Step 是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代之后似然函数都会增加,所以函数最终会收敛。
2.8.2. 举例
例子引用 Nature Biotech 的 EM tutorial 文章中的例子。
背景
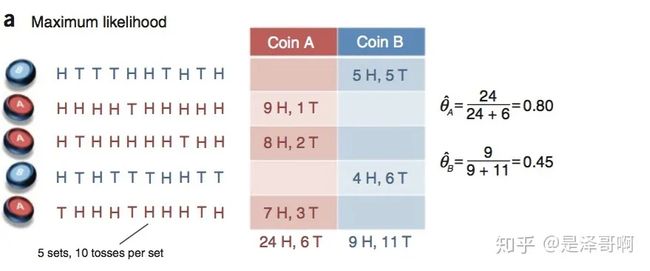
假设有两枚硬币 A 和 B,他们的随机抛掷的结果如下图所示:
我们很容易估计出两枚硬币抛出正面的概率:
θ A = 24 / 30 = 0.8 \theta _A=24/30=0.8 θA=24/30=0.8
θ B = 9 / 20 = 0.45 \theta _B=9/20=0.45 θB=9/20=0.45
现在我们加入隐变量,抹去每轮投掷的硬币标记:
碰到这种情况,我们该如何估计 θ A \theta_A θA 和 θ B \theta_B θB的值?
我们多了一个隐变量 $Z=(z_1,z_2,z_3,z_4,z_5) $,代表每一轮所使用的硬币,我们需要知道每一轮抛掷所使用的硬币这样才能估计 θ A \theta_A θA 和 θ B \theta_B θB 的值,但是估计隐变量 Z 我们又需要知道 θ A \theta_A θA 和 θ B \theta_B θB 的值,才能用极大似然估计法去估计出 Z。这就陷入了一个鸡生蛋和蛋生鸡的问题。
其解决方法就是先随机初始化 θ A \theta_A θA 和 θ B \theta_B θB ,然后用去估计 Z, 然后基于 Z 按照最大似然概率去估计新的 θ A \theta_A θA 和 θ B \theta_B θB ,循环至收敛。
计算
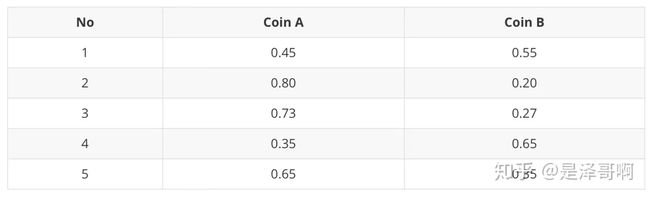
随机初始化 θ A = 0.6 \theta_A=0.6 θA=0.6 和 θ B = 0.5 \theta_B=0.5 θB=0.5
对于第一轮来说,如果是硬币 A,得出的 5 正 5 反的概率为: 0.65∗0.45 ;如果是硬币 B,得出的 5 正 5 反的概率为: 0.55∗0.55 。我们可以算出使用是硬币 A 和硬币 B 的概率分别为:
P A = 0. 6 5 ∗ 0. 4 5 ( 0. 6 5 ∗ 0. 4 5 ) + ( 0. 5 5 ∗ 0. 5 5 ) = 0.45 P_A=\frac{0.6^5*0.4^5}{(0.6^5*0.4^5)+(0.5^5*0.5^5)}=0.45 PA=(0.65∗0.45)+(0.55∗0.55)0.65∗0.45=0.45
P B = 0. 5 5 ∗ 0. 5 5 ( 0. 6 5 ∗ 0. 4 5 ) + ( 0. 5 5 ∗ 0. 5 5 ) = 0.55 P_B=\frac{0.5^5*0.5^5}{(0.6^5*0.4^5)+(0.5^5*0.5^5)}=0.55 PB=(0.65∗0.45)+(0.55∗0.55)0.55∗0.55=0.55
从期望的角度来看,对于第一轮抛掷,使用硬币 A 的概率是 0.45,使用硬币 B 的概率是 0.55。同理其他轮。这一步我们实际上是估计出了 Z 的概率分布,这部就是 E-Step。
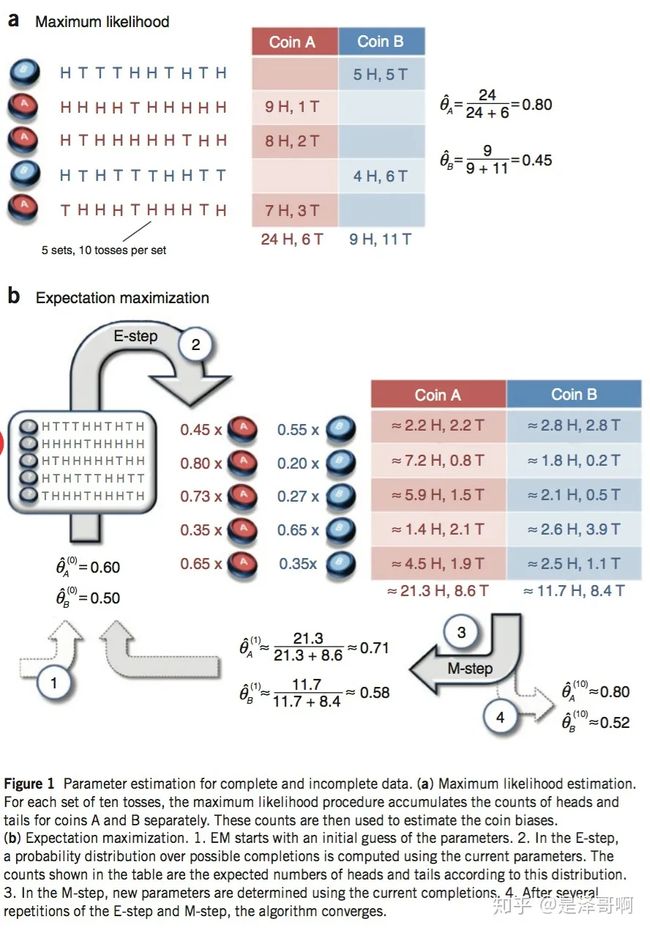
结合硬币 A 的概率和上述投掷结果(如(9H1T),我们利用期望可以求出硬币 A 和硬币 B 的贡献。以第二轮硬币 A 为例子,计算方式为:
H : 0.8 ∗ 9 = 7.2 H:0.8*9=7.2 H:0.8∗9=7.2
T : 0.80 ∗ 1 = 0.8 T:0.80*1=0.8 T:0.80∗1=0.8
于是我们可以得到:
然后用极大似然估计来估计新的 θ A \theta_A θA 和 θ B \theta_B θB。
θ A = 21.3 21.3 + 8.6 = 0.71 \theta_A=\frac{21.3}{21.3+8.6}=0.71 θA=21.3+8.621.3=0.71
θ B = 11.7 11.7 + 8.4 = 0.58 \theta_B=\frac{11.7}{11.7+8.4}=0.58 θB=11.7+8.411.7=0.58
这步就对应了 M-Step,重新估计出了参数值。
如此反复迭代,我们就可以算出最终的参数值。
详细描述如下图:
2.8.3. 推导
详细见:【机器学习】EM——期望最大(非常详细) - 知乎 (zhihu.com)
2.8.5. 应用
EM 的应用有很多,比如、混合高斯模型、聚类、HMM 等等。
2.9 随机森林
集成学习模型,是机器学习中非常重要的组成部分。其核心思想是,将多个模型组合在一起,从而产生更强大的模型。随机森林模型,是一个非常典型的集成学习模型。
2.9.1 集成模型简介
集成学习模型使用一系列弱学习器(也称为基础模型或基模型)进行学习,并将各个弱学习器的结果进行整合,从而获得比单个学习器更好的学习效果。
集成学习模型的常见算法有Bagging算法和Boosting算法。Bagging算法的典型机器学习模型为随机森林模型,而Boosting算法的典型机器学习模型为AdaBoost、GBDT、XGBoost和LightGBM模型。
2.9.2 Bagging算法
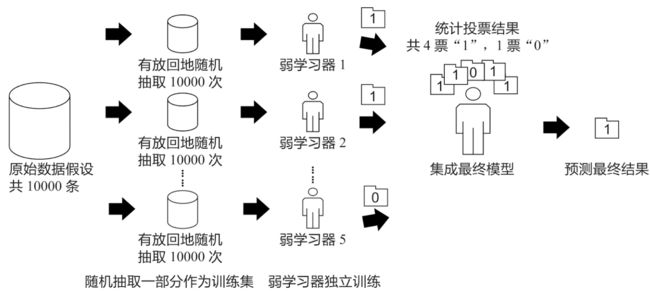
Bagging算法的原理类似投票,每个弱学习器都有一票,最终根据所有弱学习器的投票,按照少数服从多数的原则产生最终结果。如下图所示:
假设原始数据共有10000条,从中随机有放回地抽取10000次数据构成一个新的训练集(因为是随机有放回抽样,所以可能出现某一条数据多次被抽中,也有可能某一条数据一次也没有被抽中),每次使用一个训练集训练一个弱学习器。这样有放回地随机抽取n次后,训练结束时就能获得由不同的训练集训练出的n个弱学习器,根据这n个弱学习器的预测结果,按照“少数服从多数”的原则,获得一个更加准确、合理的最终预测结果。
具体来说,在分类问题中是用n个弱学习器投票的方式获取最终结果,在回归问题中则是取n个弱学习器的平均值作为最终结果。
bagging的集合策略也比较简单,对于分类问题,通常使用简单投票法,得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题,通常使用简单平均法,对T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。
由于Bagging算法每次都进行采样来训练模型,因此泛化能力很强,对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些,也就是模型的偏倚会大一些。
Bagging 的算法描述如下图所示:
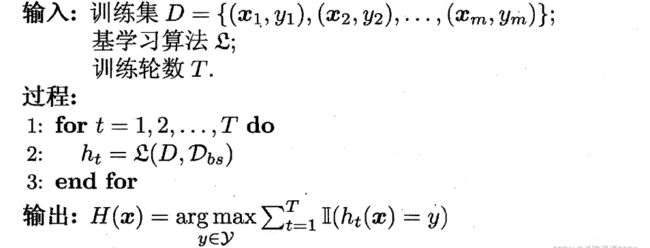
2.9.3 Boosting算法
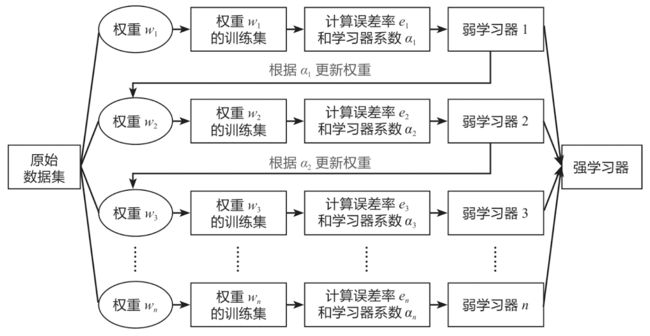
Boosting算法的本质是将弱学习器提升为强学习器,它和Bagging算法的区别在于:Bagging算法对待所有的弱学习器一视同仁,而Boosting算法则会对弱学习器“区别对待”。通俗来讲就是注重“培养精英”和“重视错误”。
“培养精英”就是每一轮训练后对预测结果较准确的弱学习器给予较大的权重,对表现不好的弱学习器则降低其权重。这样在最终预测时,“优秀模型”的权重是大的,相当于它可以投出多票,而“一般模型”只能投出一票或不能投票。
“重视错误”就是在每一轮训练后改变训练集的权值或概率分布,通过提高在前一轮被弱学习器预测错误的样例的权值,降低前一轮被弱学习器预测正确的样例的权值,来提高弱学习器对预测错误的数据的重视程度,从而提升模型的整体预测效果。上述原理如下图所示:
F m ( x ) = F m − 1 ( x ) + a r g m i n h ∑ i = 1 n L ( y i , F m − 1 ( x i ) + h ( x i ) ) F_m(x)=F_{m-1}(x)+argmin_h\sum^n_{i=1}L(y_i,F_{m-1}(x_i)+h(x_i)) Fm(x)=Fm−1(x)+argminhi=1∑nL(yi,Fm−1(xi)+h(xi)) 【加入树之后,每次需要评估加入新的树之后,是否能够使得损失下降】
2.9.4 Stacking模型
- 堆叠模型,概念比较简单:将各种分类器都使用于一个模型上,其可以堆叠各种各样的分类器(KNN,SVM,RF等等)
- 其整体流程分阶段:第一阶段通过堆叠各种模型(LNDT,RF)等得到一个分类结果,然后第二阶段利用前一个阶段的输出作为新的输入
- 注意,堆叠模型确实能使得准确率提升,但是速度是一个问题,只有在关注结果的时候,会考虑使用
2.9.5 随机森林模型的基本原理
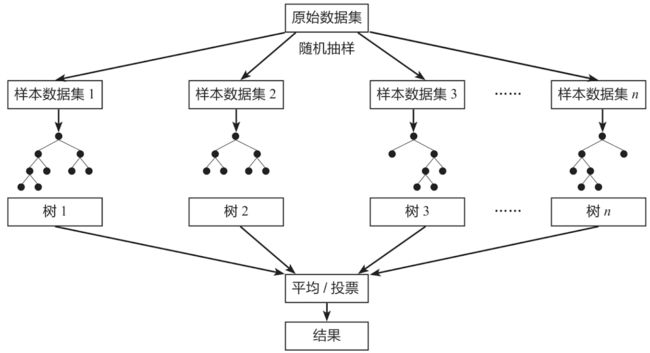
随机森林(Random Forest)是一种经典的Bagging模型,其弱学习器为决策树模型]。如下图所示,随机森林模型会在原始数据集中随机抽样,构成n个不同的样本数据集,然后根据这些数据集搭建n个不同的决策树模型,最后根据这些决策树模型的平均值(针对回归模型)或者投票情况(针对分类模型)来获取最终结果。
为了保证模型的泛化能力,随机森林模型在建立每棵树时,往往会遵循数据随机和特征随机两个基本原则。
2.9.6 数据随机
从所有数据当中有放回地随机抽取数据作为其中一个决策树模型的训练数据。例如,有1000个原始数据,有放回地抽取1000次,构成一组新的数据,用于训练某一个决策树模型。
2.9.7 特征随机
如果每个样本的特征维度是M,指定一个常数k
与单独的决策树模型相比,随机森林模型由于集成了多个决策树,其预测结果会更准确,且不容易造成过拟合现象,泛化能力也更强。
2.10 AdaBoost
2.10.1 AdaBoost算法的核心思想
AdaBoost算法(Adaptive Boosting)是一种有效而实用的Boosting算法,它以一种高度自适应的方式按顺序训练弱学习器。针对分类问题, AdaBoost算法根据前一次的分类效果调整数据的权重,在上一个弱学习器中分类错误的样本的权重会在下一个弱学习器中增加,分类正确的样本的权重则相应减少,并且在每一轮迭代时会向模型加入一个新的弱学习器。不断重复调整权重和训练弱学习器,直到错误分类数低于预设值或选代次数达到指定最大值,最终得到一个强学习器。简单来说,AdaBoost算法的核心思想就是调整错误样本的权重,进而选代升级。
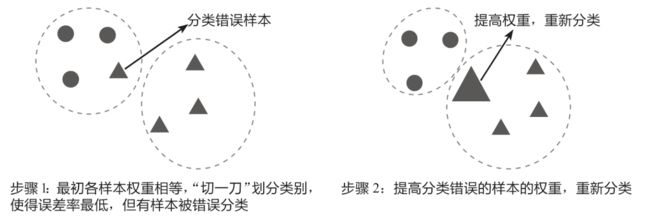
可以借助下图来理解调整权重的概念:在步骤1中先对数据进行分类,此时将小三角形错误地划分到了圆形类别中;在步骤2中调整分类错误的小三角形的权重,使它变成一个大三角形,这样它和三角形类型的数据就更加接近了,在重新分类时,它就能被准确地划分到三角形类别中。
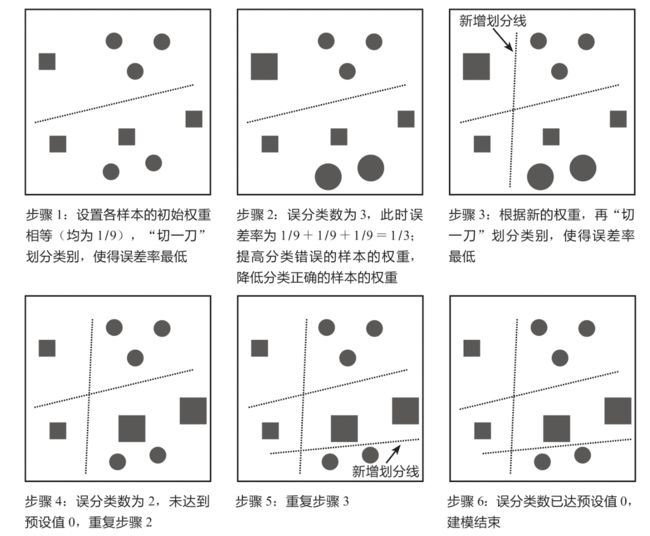
上图反映的是AdaBoost算法的核心思想。如下图所示为更复杂的AdaBoost算法示例,其核心思想和上图一致,这里仅简单演示其运作过程。预先设置AdaBoost算法在误分类数为0(即误差率为0)时终止选代,误差率等于分类错误的样本的权重之和,例如,对于9个样本,每个样本的权重为1/9,若有2个样本分类错误,那么此时的误差率为1/9+1/9=2/9。
2.10.2 AdaBoost算法的数学原理
了解AdaBoost算法的核心思想后,下面结合具体的分类问题,讲解AdaBoost算法的数学原理。这部分内容较为复杂,如果感觉理解起来有困难,可以跳过,直接学习后面的实战案例。
AdaBoost分类算法的流程图如下图所示:
输入训练数据集, T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } T=\{(x_1,y_1), (x_2,y_2),...,(x_n,y_n)\} T={(x1,y1),(x2,y2),...,(xn,yn)} ,x为特征变量,y为目标变量,其中 x i ∈ R n x_i\in{R^n} xi∈Rn , y i ∈ { − 1 , 1 } y_i\in\{-1, 1\} yi∈{−1,1} 。
下面是具体的算法过程:
Step 1: 初始化各样本的权重(样本权重相等)
w 1 i = 1 N w_{1i}=\frac{1}{N} w1i=N1
Step 2: 计算误差率
根据误差率 e m e_m em 的计算公式,构造误差率最小的弱学习器 F m ( x ) F_m(x) Fm(x) 。
e m = ∑ i = 1 N w m i I ( F m ( x i ) ≠ y i ) e_m = \sum^{N}_{i=1}w_{mi}I(F_m(x_i)\ne{y_i}) em=i=1∑NwmiI(Fm(xi)=yi)
误差率 e m e_m em 是分类错误的样本的权重之和。其中w是样本i的权重; F m ( x i ) F_m (x_i) Fm(xi) 是弱学习器 F m ( x ) F_m (x) Fm(x) 所预测的样本i的分类,即预测值。 y i y_i yi 是样本i的实际值; I ( F m ( x i ) ≠ y i ) I(F_m(x_i) \ne y_i) I(Fm(xi)=yi) 是一个指示函数(Indicator Function),当括号内的条件成立(即预测失败)时,函数取值为1,否则(即预测成功)取值为0。例如,有5个样本,每个样本的权重为1/5,若前3个样本分类错误,那么此时的误差率为1/5x 1+1/5x1+1/5x1+1/5x0+1/5x0=3/5。
Step 3: 调整弱学习器的权重
有了误差率之后,就可以调整原来的弱学习器的权重了。弱学习器 F m ( x ) F_m (x) Fm(x) 的系数 a m a_m am 的计算公式如下:
a m = 1 2 l n 1 − e m e m a_m = \frac{1}{2}ln\frac{1-e_m}{e_m} am=21lnem1−em
【 l n x lnx lnx函数是递增函数,上下同除 e m e_m em可以得到 l n ( 1 e m − 1 ) ln(\frac{1}{e_m}-1) ln(em1−1),因此误差率越大,弱学习器的权重越小;误差率越小弱分类器的权重越大】
得到第m次迭代的强学习器,公式如下:
f m ( x ) = ∑ i = 1 m a m F i ( x ) f_m(x) = \sum^m_{i=1}a_mF_i(x) fm(x)=i=1∑mamFi(x)
Step 4: 更新样本的权重
有了弱学习器的权重后,就可以更新原来样本的权重。这也是AdaBoost算法的核心所在:增大分类错误的样本的权重,减小分类正确的样本的权重,从而实现更为准确的分类。
样本权重的更新公式如下:
w m + 1 , i = w m , i Z m e x p ( − a m y i F m ( x i ) ) ( i = 1 , 2 , . . . , N ) w_{m+1,i} = \frac{w_m,i}{Z_m}exp(-a_my_iF_m(x_i)) \quad\quad (i=1,2,...,N) wm+1,i=Zmwm,iexp(−amyiFm(xi))(i=1,2,...,N)
其中:
∑ i = 1 N w m + 1 , i = 1 \sum^N_{i=1}w_{m+1,i}=1 i=1∑Nwm+1,i=1
且 y i 的取值范围为 { − 1 , 1 } , F m ( x i ) 的取值范围也为 { − 1 , 1 } y_i的取值范围为\{-1,1\},F_m(x_i)的取值范围也为\{-1,1\} yi的取值范围为{−1,1},Fm(xi)的取值范围也为{−1,1}
w m + 1 , i w_{m+1,i} wm+1,i 是本次更新的样本权重, w m i w_{mi} wmi 是上次的样本权重,各样本权重之和是1。 a m a_m am 是第m次迭代中弱学习器 F m ( x ) F_m(x) Fm(x) 的系数, y i y_i yi 是样本i的实际值, F m ( x i ) F_m(x_i) Fm(xi) 是弱学习器 F m ( x ) F_m(x) Fm(x) 所预测的样本i的分类, Z m Z_m Zm 是一个规范化因子,其公式如下:
Z m = ∑ i = 1 N w m i e x p ( − a m y i F m ( x i ) ) Z_m = \sum^N_{i=1}w_{mi}exp(-a_my_iF_m(x_i)) Zm=i=1∑Nwmiexp(−amyiFm(xi))
这里的 e x p ( x ) exp(x) exp(x) 为指数函数 e x e^x ex 的另一种写法。
Step 5: 反复迭代
将上面的过程反复选代,直到误分类数达到阅值或选代次数达到设定的最大值。M次选代后得到最终强学习器如下:
s i g n [ f M ( x ) ] = s i g n [ ∑ i = 1 M a i F i ( x ) ] sign[f_M(x)]=sign\left[\sum^M_{i=1}a_iF_i(x)\right] sign[fM(x)]=sign[i=1∑MaiFi(x)]
其中 s i g n ( x ) sign(x) sign(x) 是符号函数,即:
s i g n ( x ) = { 1 , x > 0 0 , x = 0 − 1 , x < 0 sign(x) = \begin{cases} \ \ 1,\quad x > 0 \\ \ \ 0,\quad x = 0 \\ -1, \quad x< 0 \end{cases} sign(x)=⎩ ⎨ ⎧ 1,x>0 0,x=0−1,x<0
至此,AdaBoost算法的数学原理介绍完毕。
2.10.3 补充知识:正则化项
为防止AdaBoost算法过拟合,可以向模型加入正则化项。即,每个弱学习器的权重缩减系数 υ \upsilon υ ,又称为learning rage(学习率)。
弱学习器的迭代公式:
f m ( x ) = ∑ i = 1 m a m F i ( x ) f_m(x) = \sum^m_{i=1}a_mF_i(x) fm(x)=i=1∑mamFi(x)
加入权重缩减系数后公式变为:
f m ( x ) = ∑ i = 1 m υ a m F i ( x ) f_m(x) = \sum^m_{i=1}{\upsilon}a_mF_i(x) fm(x)=i=1∑mυamFi(x)
权重缩减系数 υ \upsilon υ 的取值范围为(0, 1]。取值较小意味着要达到一定的误分类数或学习效果,需要的选代次数更多,需要训练的弱学习器更多;取值较大意味着要获得相同的学习效果,需要的选代次数更少,需要训练的弱学习器更少。
2.11 GBDT、XGBoost、LightGBM
详细见:系列教程 (showmeai.tech)