bzoj2300【HAOI2011】防线修建

2300: [HAOI2011]防线修建

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 696  Solved: 384
[ Submit][ Status][ Discuss]

Description

近来A国和B国的矛盾激化，为了预防不测，A国准备修建一条长长的防线，当然修建防线的话，肯定要把需要保护的城市修在防线内部了。可是A国上层现在还犹豫不决，到底该把哪些城市作为保护对象呢？又由于A国的经费有限，所以希望你能帮忙完成如下的一个任务：

1.给出你所有的A国城市坐标

2.A国上层经过讨论，考虑到经济问题，决定取消对i城市的保护，也就是说i城市不需要在防线内了

3.A国上层询问对于剩下要保护的城市，修建防线的总经费最少是多少

你需要对每次询问作出回答。注意单位1长度的防线花费为1。

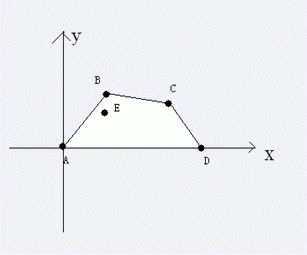
A国的地形是这样的，形如下图，x轴是一条河流，相当于一条天然防线，不需要你再修建

A国总是有两个城市在河边，一个点是(0,0)，一个点是(n,0)，其余所有点的横坐标均大于0小于n，纵坐标均大于0。A国有一个不在(0,0)和(n,0)的首都。(0,0),(n,0)和首都这三个城市是一定需要保护的。

上图中，A,B,C,D,E点为A国城市，且目前都要保护，那么修建的防线就会是A-B-C-D，花费也就是线段AB的长度+线段BC的长度+线段CD的长度,如果，这个时候撤销B点的保护，那么防线变成下图

Input

第一行，三个整数n,x,y分别表示河边城市和首都是(0,0)，(n,0)，(x,y)。

第二行，一个整数m。

接下来m行，每行两个整数a,b表示A国的一个非首都非河边城市的坐标为(a,b)。

再接下来一个整数q，表示修改和询问总数。

接下来q行每行要么形如1 i，要么形如2，分别表示撤销第i个城市的保护和询问。

Output

对于每个询问输出1行，一个实数v，表示修建防线的花费，保留两位小数

Sample Input

4 2 1
2
1 2
3 2
5
2
1 1
2
1 2
2

Sample Output

6.47
5.84
4.47

HINT

m<=100000,q<=200000,n>1

所有点的坐标范围均在10000以内, 数据保证没有重点

凸包上删点很难处理，所以我们考虑离线，将删点操作转化为加点操作。

于是现在问题变成了：维护一个支持加点操作的动态凸包。

每次加一个点判断是否在凸包内，然后用set找两边相邻的点，再两边分别维护。

#include
#include
#include
#include
#include
#include
#include
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
#define maxn 200005
using namespace std;
int n,x,y,m,q;
int opt[maxn];
bool tag[maxn];
double now,ans[maxn];
struct data{int x,y;}a[maxn];
set s;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
inline double dis(data a,data b)
{
	return sqrt((double)(a.x-b.x)*(a.x-b.x)+(double)(a.y-b.y)*(a.y-b.y));
}
inline data operator -(data a,data b)
{
	return (data){a.x-b.x,a.y-b.y};
}
inline int operator *(data a,data b)
{
	return a.x*b.y-a.y*b.x;
}
inline bool operator <(data a,data b)
{
	return a.x==b.x?a.y::iterator l=s.lower_bound(x),r=l,t;
	l--;
	if ((*r-*l)*(x-*l)<0) return;
	now-=dis(*l,*r);
	for(;;)
	{
		t=r;r++;
		if (r==s.end()) break;
		if ((*r-x)*(*t-x)>0) break;
		now-=dis(*t,*r);
		s.erase(t);
	}
	for(;;)
	{
		if (l==s.begin()) break;
		t=l;l--;
		if ((x-*l)*(*t-*l)>0) break;
		now-=dis(*t,*l);
		s.erase(t);
	}
	s.insert(x);
	l=r=s.find(x);l--;r++;
	now+=dis(*l,x)+dis(*r,x);
}
int main()
{
	n=read();x=read();y=read();
	s.insert((data){0,0});s.insert((data){n,0});s.insert((data){x,y});
	now=dis((data){0,0},(data){x,y})+dis((data){n,0},(data){x,y});
	m=read();
	F(i,1,m) a[i].x=read(),a[i].y=read();
	q=read();
	F(i,1,q)
	{
		int flg=read();
		opt[i]=(flg==2)?0:read();
		if (opt[i]) tag[opt[i]]=true;
	}
	F(i,1,m) if (!tag[i]) add_data(a[i]);
	D(i,q,1)
	{
		if (opt[i]) add_data(a[opt[i]]);
		else ans[i]=now;
	}
	F(i,1,q) if (!opt[i]) printf("%.2lf\n",ans[i]);
	return 0;
}