NOIP2017模拟赛(1) 总结

a 多色彩的巧克力

题目描述

奶牛Bessie有N块巧克力，从左往右排成一行，编号从0到N-1。第i块巧克力的颜色是color[i]。我们定义一个参数MaxLen,它表示：具有相同颜色的连续一段巧克力的最大长度。例如：有10块巧克力，颜色分别是: ADDDABBAAB,那么MaxLen=3,因为有3块颜色是D的巧克力，而且这3块巧克力的位置是连续的。为了使得MaxLen最大，Bessie可以交换相邻两块巧克力的位置，但是Bessie 总共交换的次数不能超过给定的值swap。那么MaxLen的最大值是多少？

---

输入格式

多组测试数据。
第一行，一个整数G，表示有G组测试数据。1 <= G <=5。
每组测试数据格式如下：
第一行，两个整数N、swap 。1 <= N <= 50。 1 <= swap <= 2500。
第二行，N个大写字母，第i个字母表示第i块巧克力的颜色。

---

输出格式

共G行，每行一个整数。

---

输入样例

4
7 1
ABCDCBC
7 2
ABCDCBC
9 3
ABBABABBA
9 4
ABBABABBA

---

输出样例

2
3
4
5

---

【样例解释】

第二组测试数据：交换后可以变成ABDCCCB。
第三组测试数据：交换后可以变成ABBBBAABA。
第四组测试数据：交换后可以变成AABBBBBAA。

---

解题思路(模拟+贪心)

这题作为本场测试的第一题，是拿来签到的。
一开始想dp，后来发现可以贪心，枚举不动点，然后将左右两端的与其相同颜色的巧克力向中间拉，然后每次判断选最近的拉过来，直到达到最大交换次数为止，同时统计长度更新答案。
时间复杂度: O(n2)
其实还有根据“中位数定理”然后发现枚举中的单调性，将同颜色的分为一类，每次快速维护变化的信息，然后将时间复杂度降为 O(nlogn) 或 O(n) 的更优的方法。但是对于此题而言，平方足矣。听说 O(n5) 都能水过。

---

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define N 55

using namespace std;

int G, n, S, Ans;
char ch[55];

int main(){

    freopen("a.in", "r", stdin);
    freopen("a.out", "w", stdout);

    scanf("%d", &G);
    while(G --){
      Ans = 0;
      scanf("%d%d", &n, &S);
      scanf("%s", &ch);
      for(int i = 0; i < n; i++){
        int L, R, temp = 0;
        L = R = i;
        int j = i-1, k = i+1;
        while(j >= 0 || k < n){
          while(j >= 0 && ch[i] != ch[j])  j --;
          while(k < n && ch[i] != ch[k])  k ++;

          if(j >= 0 && (L - j - 1 <= k - R - 1 || k >= n)){
            if(temp + L - j - 1 > S)  break;
            temp += L - j - 1;
            L --;
            j --;
          }  
          else if(k < n && (L - j - 1 > k - R - 1 || j < 0)){
            if(temp + k - R - 1 > S)  break;
            temp += k - R - 1;
            R ++;
            k ++;
          }
        }
        Ans = max(Ans, R - L + 1);
      }
      printf("%d\n", Ans);
    }

    return 0;
}

---

b 砖块II

题目描述

有K种不同规则的长方体砖块，长宽高分别是：1×1×1、2×1×1、3×1×1…，K×1×1.还给出一个W×1×1的地基，如下图所示，W=9, k=3,下面的是地基:

现在你要在地基上堆放砖块，必须满足如下的规则：
1、 砖块只能横放，不能竖放。
2、 砖块必须放置在整数位置，且不能越出地基。
3、 砖块任何部分的正下方都必须要有其他砖块或者是地基。
例如：下图是不合法的放置方式，有4个不合法的地方：

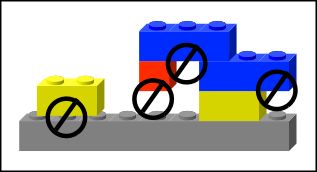
我们定义一种堆放砖块方案的高度height：它是指该方案中最高的砖块是第几层，其中地基是第0层，例如（图二）的高度是3。
我们定义不同的堆放方案：例如有两种堆放方案A和B，只要满足两个条件之一，方案A和方案B就是不同的方案：
1、 在某个位置方案A有砖块而方案B在该位置没有砖块，或者方案B有砖块而方案A没有。
2、 在某个位置方案A和方案B都有砖块，但是它们不是同一种规格的砖块。

给定地基的长度W，和地砖的最大长度K，你的任务是计算有多少种不同的堆放砖块的方案，你的堆放砖块方案的高度height不能超过给定的H。答案模1000000007。
例如：下图是W=3, k=3, H=2的所有合法方案：

---

输入格式

多组测试数据。
第一行，一个整数G，表示有G组测试数据。1 <= G <=3。
每组测试数据格式如下：
一行，三个整数W、H、K 。1 <= W, H <= 50。 1 <= K <= W

---

输出格式

共G行，每行一个整数。

---

输入样例

3
3 1 3
3 2 3
10 10 3

---

输出样例

13
83
288535435

---

解题思路(dp)

这题是这场测试中较难的一道题。由于算方案数，我们考虑dp。
考试时没有想出子问题与转移，证明我的思维深度与广度还是远不及人。
我们记 f[i][j] 表示搭i层，地基（结束点）为j时的方案数。
这样记方案数很重要，很简洁而且很快就能找出子问题，如果是乱记的话非常不易处理，因为每种搭法不仅有形状还有颜色。
我们仔细观察题目中给出的图可以发现一个特点，当地基确定后，我们相当于是在上面建造一些互不相挨着的建筑。每一栋建筑确定地基后又是再建子建筑。
于是我们找到了子问题，那情况就分为2种，要么这地基上不建，作为屋顶。要么建，就往上面摆砖。
枚举连续的一段建屋子，然后预处理固定形状的颜色的方案数s，借助其进行转移就行了。
预处理: f[i][0]=1; 　作为屋顶： f[0][i]=1;
连续建k个时: f[i][j]+=f[i−1][k]∗s[k]∗f[i][max(j−k−1,0)];
注意这里j-k-1是为了避免重复计算，挨在一起的建筑就当作一个算，做到不重不漏。
当然别忘了此处不建的情况 f[i][j]+=f[i][j−1];
这题的难点在于如何确定子问题，还有，别忘了多mod。
时间复杂度： O(H∗W∗W)

---

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define N 55
#define Mod 1000000007

using namespace std;

typedef long long LL;
int G, w, h, K;
LL s[N], f[N][N];

int main(){

    freopen("b.in", "r", stdin);
    freopen("b.out", "w", stdout);

    scanf("%d", &G);

    while(G --){
      scanf("%d%d%d", &w, &h, &K);
      s[0] = 1;
      for(int i = 1; i <= w; i++){
        s[i] = 0;
        for(int j = max(i-K, 0); j < i; j++)
          s[i] = (s[i] + s[j]) % Mod;
      }

      for(int i = 1; i <= w; i++)  f[0][i] = 1;
      for(int i = 1; i <= h; i++){
        f[i][0] = 1;
        for(int j = 1; j <= w; j++){
          f[i][j] = f[i][j-1];
          for(int k = 1; k <= j; k++)
            f[i][j] = (f[i][j] + f[i-1][k]*s[k]%Mod*f[i][max(j-k-1, 0)]%Mod) % Mod;
        }
      }
       printf("%lld\n", f[h][w]);
    }
    return 0;
}

---

c 火灾

题目描述

Farmer John 有一个宽是w单位，高是h单位的草莓园。则草莓园被分成w * h格. 突然间，某些格子起火了，Farmer John马上打电话给火警. 每过一个小时，着火的格子的附近格子也会着火 (上下左右和对角线)，如下图所示：

你可以看到，刚开始只有两个格子有火，3小时后所有格子都着火了. 如果火警2小时后赶到,那么就可以挽救6个格子.如果火警1小时后赶到, 就可以挽救12个格子, 如果火警即刻赶到(即0小时)，那么可以挽救 23 个格子。
现在Farmer John至少要保留 need 个格子，求火警察最迟可以几个小后赶到？

---

输入格式

多组测试数据。
第一行：一个整数ng, 1 <= ng <= 5. 表示有ng组测试数据。
每组测试数据格式如下：
第一行：三个整数: w 、h、need. 1 <= w、h <= 10^9
第二行：一个整数N,表示一开始有多少个格子是着火的。不会重复
1 <= N <= 50
接下来有N行，每行两个整数X、Y,表示单元格（X,Y）一开始就着火了。 1 <= X <= w, 1 <= Y <= h
注意： 1 <= need <= w * h － N

---

输出格式

Farmer John至少要保留 need 个格子，求火警察最迟可以几个小后赶到。
ng行，每行对应一组输入数据。

---

输入样例

2
5 5 12
2
1 4
2 2
101 101 400
1
51 51

---

输出样例

1　（就是题目的例子）
49

---

解题思路(二分答案+扫描线)

这题一看答案就满足单调性，这不用说。直接往二分上想。
知道经过了T秒后，地图变成什么样了呢？由于没个时刻的那一片火海都呈正方形向四周扩散，所以剩下的就是一些知道边长与位置的矩形(受边界影响)，求它们的面积并。
然而说起来容易，不就是在写一个网格上的平面扫描吗？然而我一开始却想去了半平面交，真是无语了。。
就算写扫描线也没有想象中那样順畅，我也写了挺久的，主要有以下几个原因:
①我一开始直接那网格的“边”作为矩形的边，这样边就有面积了，哪里该算哪里不该算也是挺烦的。还好后来以边界为边，好做多了。
②控制矩形的进出时一定要注意边界情况，打标记之类的，建议写完对拍一下或多出几组数据。
③最令人头疼也是最容易错的是将二维平面降维变成一维区间相交问题时一定不要搞错，在这题上我一开始就忘了将以前的区间按L插排一下，结果就GG了。
总结就是这种细节题要多些多注意。还有我写的是极为暴力的扫描，没有离散化的，其实离散化后更好做，加上线段树可以将 O(n2) 降为 O(nlogn) 的，不过在这题，暴力+插排就够了。
ps：lgj大大还有一种直接离散化硬做不用扫描法的求矩形的面积并的方法。。。

---

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define N 55

using namespace std;

typedef long long LL;
int ng, n, cnt, w, h, used[N];
LL need, square;
struct Data{
    int x, y;
}fire[N];

struct Line{
    int L, R, h, id;
    Line() {}
    Line(int L, int R, int h, int id):L(L), R(R), h(h), id(id) {}
    bool operator < (const Line& Q) const{
      if(h == Q.h)  return L < Q.L;
      return h < Q.h;
    }
}ll[N<<1];


bool Judge(int r){
    cnt = 0;
    for(int i = 1; i <= n; i++){
      ll[++cnt] = Line(max(1, fire[i].x - r), min(w+1, fire[i].x + r + 1), max(1, fire[i].y - r), i);
      ll[++cnt] = Line(max(1, fire[i].x - r), min(w+1, fire[i].x + r + 1), min(h+1, fire[i].y + r + 1), i);
      used[i] = 0;
    }

    sort(ll+1, ll+cnt+1);

    square = 0;
    for(int i = 1; i < cnt; i++){
      if(used[ll[i].id] == 1)  used[ll[i].id] = -1;
      else  used[ll[i].id] = 1;


      int pos = i;
      Line temp = ll[i];
      for(int j = i-1; j > 0; j--)  if(ll[j].L > ll[i].L)  pos = j;
      for(int j = i; j > pos; j--)  ll[j] = ll[j-1];
      ll[pos] = temp;

      int Len = 0, Right = 0;
      for(int j = 1; j <= i; j++){
        if(used[ll[j].id] != -1){
          if(ll[j].R <= Right)  continue;
          if(ll[j].L <= Right)  Len += ll[j].R - Right;
          else  Len += ll[j].R - ll[j].L;
          Right = max(Right, ll[j].R);
        } 
      }

      square += (LL)Len * (LL)(ll[i+1].h - temp.h);
    }
    return (LL)w * (LL)h - square >= need;
}

int main(){

    freopen("c.in", "r", stdin);
    freopen("c.out", "w", stdout);

    scanf("%d", &ng);

    while(ng --){
      scanf("%d%d%lld", &w, &h, &need);
      scanf("%d", &n);
      for(int i = 1; i <= n; i++)  scanf("%d%d", &fire[i].x, &fire[i].y);
      int L = 0, R = max(w, h);
      while(L + 1 < R){
        int mid = (L + R) >> 1;
        if(Judge(mid))  L = mid;
        else  R = mid;
      }
      printf("%d\n", L);
    }

    return 0;
}

---

总结

只会做傻逼题的我，果真没得救啊，智商捉急啊，编程能力还需进一步提高，遇到题有思路但不敢写的情况要尽量减少。

---

给岁月以文明，给时光以生命。