NOIP2017模拟赛(8) 总结

前言：这次KsCla和hzh神犇们又AK了，我才100+53+100=253，连这也是目前的最好成绩了，我看到差距，我将奋起直追，调整考试状态。
努力还是太少太少了。

---

a 路径

题目描述

在二维坐标平面里有N个整数点，Bessie要访问这N个点。刚开始Bessie在点（0，0）处。 每一步，Bessie可以走到上、下、左、右四个点。即假设Bessie当前所在点的坐标是(x,y),那么它下一步可以移动到(x,y+1), (x,y-1), (x+1,y), (x-1,y)之一。
Bessie目标是找到一个移动序列，满足下面的条件：
1、从点(0,0)出发。
2、对于给定的那N个点，每个点至少被访问一次。
3、可以选择那N个给定点中任意一个作为结束点。
现在为了增加难度，农夫规定Bessie走过的所有步数之和的奇偶性必须为wantedParity,显然wantedParity 是0或1，是题目给定的，0表示偶，1表示奇。Bessie立刻感觉到了难度的增加，如果存在满足条件的移动序列，那么输出CAN，否则输出CANNOT。

---

输入格式

多组测试数据。
第一行，一个整数g，表示有g组测试数据，1 <= g <= 5。
每组测试数据格式：
第一行，N、wantedParity。 1 <= N <= 50。
接下来有N行，每行两个整数：x, y，表示第i个点的坐标值。
范围都在【-1000000，1000000】。输入的N个点不会有重叠，且不会有（0，0）点。

---

输出格式

共g行，每行输出CAN或CANNOT。

---

输入样例

5
4 0
-1 -1
-1 1
1 1
1 -1
3 1
-5 2
-3 0
2 3
2 1
1001 0
-4000 0
3 0
11 -20
21 42
0 7
2 1
0 10
6 -20

---

输出样例

CAN
CAN
CAN
CANNOT
CANNOT

样例解释
第一组测试数据：其中一个合法序列如下：

• 2 steps: (0,0) -> (-1,-1).
• 2 steps: (-1,-1) -> (-1,1).
• 2 steps: (-1,1) -> (1,1).
• 2 steps: (1,1) -> (1,-1).

第二组测试数据：其中一个合法序列：

• 7 steps: (0,0) -> (-5,2).
• 4 steps: (-5,2) -> (-3,0).
• 8 steps: (-3,0) -> (2,3).

第三组测试数据：其中一个合法序列：
(0,0) -> (-4000,0) -> (1001, 0)。

---

解题思路(奇偶性)

这是一道送分题，我们随便就能发现，两个格点之间无论怎么走，其步数的奇偶性都是一样的，等于其曼哈顿距离的奇偶性。感性认识一下，假设我们从一个点走到另一个点，那么如果不走曼哈顿距离的路径的话，肯定会有多余的步子向上了又向下，向左了又向右，就是说这些步一定是偶数，相互抵消。根据奇数+偶数=奇数，偶数+偶数=偶数的常识，直接 O(n) 枚举终点判断其曼哈顿距离的奇偶性就可以了。
然而既然是乱走，每个点都有充分的理由被走到了。

---

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define N 60

using namespace std;

int nG, n, want;
struct Data{
    int x, y;
    Data() {}
    Data(int x, int y):x(x), y(y) {}
}P[N];

int Getdis(Data A, Data B){
    int dis = abs(A.x - B.x) + abs(A.y - B.y);
    return dis & 1;
}

int main(){

    freopen("a.in", "r", stdin);
    freopen("a.out", "w", stdout);

    scanf("%d", &nG);
    while(nG --){
      scanf("%d%d", &n, &want);
      for(int i = 1; i <= n; i++)  scanf("%d%d", &P[i].x, &P[i].y);

      bool Sol = false;
      Data home = Data(0, 0);

      for(int i = 1; i <= n; i++)
        if(Getdis(home, P[i]) == want){
          Sol = true;
          break;
        }

      if(Sol)  printf("CAN\n");
      else  printf("CANNOT\n");
    }


    return 0;
}

---

b 冠军

题目描述

有N个拳手参加擂台赛，这个人的编号是0至N-1。有N个位置，编号从0至N-1。每个位置分配一个拳手，显然共有N!种不同的分配方案。
对于一种具体的分配方案，站在位置0的拳手与站在位置1的拳手比赛，胜者进入下一轮，败者被淘汰。站在位置2的拳手与站在位置3的拳手比赛，胜者进入下一轮，败者被淘汰，同样道理，站在位置4的拳手与站在位置5的拳手比赛，胜者进入下一轮，败者被淘汰。。。最终会产生一个冠军拳手。
如下图所示：

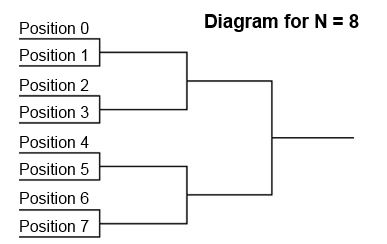
已知N一定是2的若干次幂，而且不超过16，也就是说N是{2,4,8,16}之中的某一个数。
现在的问题是：有多少种不同的分配方案，使得第i个选手能最终成为冠军？不妨假设该数值是ans[i]。
你的任务就是输出：ans[0]、ans[1]、….ans[N-1]。

---

输入格式

第一行，一个整数N。 N=2或者4或者8或者16。
接下来是N行N列的字符矩阵，第i行第j列的字符如果是’Y’，表示第i个拳手如果跟第j个拳手直接比赛的话，第i个拳手会赢第j个拳手，如果字符是‘N’，表示第i个拳手会输给第j个拳手。
注意：
1、第i行第i列的字符一定是’N’
2、拳手的胜负不一定满足传递性。例如：第i个拳手能赢第j个拳手，第j个拳手能赢第k个拳手，但第i个拳手可能会输给第k个拳手。
3、如果第i行第j列的字符是’Y’，那么第j行第i列的字符一定是’N’，即拳手i和拳手j比赛，有且只有一个胜者。

---

输出格式

共N行，第i行是ans[i]。

---

输入样例

输入样例一：

2
NN
YN

输入样例二：

4
NYNY
NNYN
YNNY
NYNN

输入样例三：

8
NYNYNYNY
NNYNYNYY
YNNNNNNN
NYYNNYNY
YNYYNYYY
NYYNNNNN
YNYYNYNN
NNYNNYYN

---

输出样例

输出样例一：

0
2

输出样例二：

8
0
16
0

输出样例三：

4096
8960
0
2048
23808
0
1408
0

【样例解释】
第一样例：不管拳手1站在位置0还是站在位置1，都能战胜拳手0。

---

解题思路(状态压缩+记忆化搜索)

这题我在考场上手写了个近乎 O(n!∗n) 的暴力，水了53分。话说这样的数据还是有点良心的。
至于正解，留坑待填。

---

c 指纹

题目描述

随着科技的发展，当今很多企业向社会推出了越来越多的结合指纹识别技术的高科技产品。其中以需要进行身份验证或身份识别类型的产品居多，如门禁系统、手提电脑、指纹硬盘。
对任何生物识别系统来说，输入数据的质量对于系准确率有着重大的影响。为了获得较高质量的指纹图像，近年来指纹采集设备不断地被更新，各种先进的指纹采集技术也逐渐被引入到实际产品中。尽管如此，由于手指皮肤情况、空气湿度、灰尘等一些因素的影响，依旧存在着大量的质量不高的指纹图像。
通常我们可以通过编号为A，B，C，D的四个属性来评估一个指纹图像的质量的高低：
A为杂点的数量；B为折痕的数量；C为脊线断续程度；D为脊线粘连程度。这四个属性值越小表示该图像在相应方面表现越优。
由于指纹图质量评估研究的需要，我们通过对一个人的指纹进行多次采样后得到多个不同质量的指纹图像，并将其各质量属性记录在一个数据库中（不同图像的各属性值均不相同）。对于两个指纹图像，单个属性的好坏并不能说明图像质量的高低。比如图像1杂点数比图像2的少，但有可能图像1的粘连程度比图像2高得多，因此不能武断地认为图像1就比图像2好。
但是如果一个图像有不少于三个属性都优于另一个图像，那么我们有理由相信前者的质量要优于后者。对于数据库中的一个指纹图像I，如果存在另一个图像J，J有不少于三个质量属性优于图像I，那么我们认为图像I是一种“累赘”。
为了减少指纹图像数据库的大小，我们希望去除其中的累赘图像，现在实验室需要你的帮忙，找出该部分图像。为方便就算，我们已经分别按四个属性，计算出了所有图像按该属性的优劣程度排序的名次。

---

输入格式

第一行，包含一个正整数N，表示有N张指纹图像，编号为1,2,3…N。1 <= N <= 100000。
接下来的N行，每行有4个正整数Ai,Bi,Ci,Di。第i行表示编号为i的图像在所有图像中，其A属性排名为Ai, B属性排名为Bi, C属性排名为Ci, D属性排名为Di。所有Ai取遍1到N这N个自然数，1表示最优，N表示最差，类似地，Bi,Ci,Di也一样。

---

输出格式

第一行，一个整数M，表示累赘的指纹图像个数。接下来有M行，每行包含一个整数，表示累赘的图像的编号。标号从小到大输出。

---

输入样例

6
1 1 2 6
2 3 3 4
3 4 1 3
4 2 6 5
5 6 5 1
6 5 4 2

---

输出样例

4
2
4
5
6

---

解题思路(快排+线段树)

本题乃一线段树果题。本人很快写完并拍了1h(data maker太弱)，然后就不虚了。
首先有四个关键字选三个， C34=4 枚举一下，假设我们要比较 A , B , C 这三个关键字，按 A 排序，这样 A 小的都在前面；再将 B 作为下标，没了离散化的烦恼；最后在对应 B 的下标中记下 C ，再用线段树维护。如果对于当前的关键字， i 前面的直接找 1 到 Bi−1 的这段区间，然后取最小值，如果比 Ci 小，那 i 必然是累赘。为它打上标记，然后对应的将 Ci 放进线段树。这样做完所有情况后，就统计答案。
这题线段树就是考察了区间求最小值，单点修改操作。很简单的数据结构题。
每次枚举线段树初始化为oo，不计线段树常数的话，时间复杂度 O(NlogN∗4) 。
ps：貌似还有其他作法，treap也能做，splay就更不用说了。

---

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define N 100010
#define oo 0x7fffffff

using namespace std;

int n, Cnt;
struct Data{
    int A, B, C, D;
    int id;
    bool operator < (const Data& Q) const{return A < Q.A;}
}gra[N], memory[N];
bool wa[N];

int tree[N<<2];

void update(int root, int L, int R, int x, int y, int v){
    if(x > R || y < L)  return;
    if(x <= L && y >= R){
      tree[root] = v;
      return;
    }
    int mid = (L + R) >> 1, Lson = root << 1, Rson = root << 1 | 1;
    update(Lson, L, mid, x, y, v);
    update(Rson, mid+1, R, x, y, v);
    tree[root] = (tree[Lson] < tree[Rson]) ? tree[Lson] : tree[Rson];
}

int query(int root, int L, int R, int x, int y){
    if(x > R || y < L)  return oo;
    if(x <= L && y >= R)  return tree[root];
    int mid = (L + R) >> 1, Lson = root << 1, Rson = root << 1 | 1;
    int temp1 = query(Lson, L, mid, x, y);
    int temp2 = query(Rson, mid+1, R, x, y);
    return (temp1 < temp2) ? temp1 : temp2;
}

int main(){

    freopen("c.in", "r", stdin);
    freopen("c.out", "w", stdout);

    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
      scanf("%d%d%d%d", &gra[i].A, &gra[i].B, &gra[i].C, &gra[i].D);
      gra[i].id = i;
    }

    for(int i = 1; i <= n; i++)  memory[i] = gra[i];

    for(int I = 1; I <= 4; I++){
      if(I == 2)  for(int i = 1; i <= n; i++)  swap(gra[i].A, gra[i].D);
      else if(I == 3)  for(int i = 1; i <= n; i++)  swap(gra[i].B, gra[i].D);
      else if(I == 4)  for(int i = 1; i <= n; i++)  swap(gra[i].C, gra[i].D);

      sort(gra+1, gra+n+1);

      for(int i = 0; i <= (n<<2); i++)  tree[i] = oo;

      for(int i = 1; i <= n; i++){
        int temp = query(1, 1, n, 1, gra[i].B);
        if(temp < gra[i].C)  wa[gra[i].id] = true;
        update(1, 1, n, gra[i].B, gra[i].B, gra[i].C);
      }
      for(int i = 1; i <= n; i++)  gra[i] = memory[i];
    }

    for(int i = 1; i <= n; i++)  if(wa[i])  Cnt ++;
    printf("%d\n", Cnt);
    for(int i = 1; i <= n; i++)  if(wa[i])  printf("%d\n", i);


    return 0;
}

---

总结

要继续努力，多学新知识，巩固旧知识，向其他的神犇学习。

---

隐约雷鸣 阴霾天空 但盼风雨来 能留你在此
隐约雷鸣 阴霾天空 即使天无雨 我亦留此地