题解 | 杂题
qwq
不知道写点啥了…就随便写写了…
[Codeforces1130E Wrong Answer]
Codeforces1130E Wrong Answer
构造
题面描述
智商严重下线 看到这题的时候一点思路也没有
qwq
第一个数设成-1 其余都是正的 为$a_1,a_2… $
记 ∑ i = 1 N a i = s u m \sum_{i=1}^{N} a_i =sum ∑i=1Nai=sum
则正确答案是 ( s u m − 1 ) ∗ ( N + 1 ) (sum-1)*(N+1) (sum−1)∗(N+1)
错误答案是 s u m ∗ N sum*N sum∗N
两个的差即为 k k k
显然这是肯定可以构造出来的
Hdu5726 GCD
大噶好我是传送门
前言
这么简单的题目我都没想到 这一定不是我
题目描述
给你一个数组 a [ ] a[] a[] ( n ≤ 1 e 5 , a [ i ] ≤ 1 e 9 n \leq 1e5,a[i] \leq 1e9 n≤1e5,a[i]≤1e9)
每次询问你一个 l , r l,r l,r
求出 g c d ( a l , a l + 1 … , a r ) gcd(a_l,a_{l+1}…,a_r) gcd(al,al+1…,ar) 还有多少对 ( L , R ) (L,R) (L,R) 使得 g c d ( a L , a L + 1 … , a R ) = g c d ( a l , a l + 1 … , a r ) gcd(a_L,a_{L+1}…,a_R) = gcd(a_l,a_{l+1}…,a_r) gcd(aL,aL+1…,aR)=gcd(al,al+1…,ar)
QwQ
其实 g c d gcd gcd是满足区间合并的性质的!
那么求 ( l , r ) (l,r) (l,r)的gcd可以用个rmq搞定~
然后我们考虑一下 对于从 i i i开始的所有区间
这些区间不同的gcd值最多也只有log级别个!
那么我们就可以直接二分求出啦。。qwq
那么总复杂度大概是 O ( n l o g n 2 ) O(nlog^2_n) O(nlogn2)
Codeforces1186C. Vus the Cossack and Strings
题目描述
给你两个01串 a , b a,b a,b 满足 l e n ( b ) ≤ l e n ( a ) ≤ 1 e 6 len(b) \leq len(a) \leq 1e6 len(b)≤len(a)≤1e6
求出 a a a的所有长度为 l e n ( b ) len(b) len(b)的子串 与 b b b字符串相同的位的个数位偶数的有多少个
题解
这一定不是我!
如果是不同的话 只有两种情况 1-0 或者0-1
那么如果相同位的位数为偶数的话 是不是相当于
两个串1的个数的奇偶性相同qwq
Codeforces1187E. Tree Painting
题面描述
给你一颗树~ 第一轮你选一个染成黑色 接下来的每一轮 你都可以染上一个黑色所相连的白色为黑色
答案为 每一轮(包括第一轮)所染的那个点所在的白色联通块的大小
问所有情况的最大值qwq
QwQ
我们可以确定的一点是 当你第一轮确定了一个点之后 那么那种情况的答案也就确定了qwq
那么我们不断得移动第一个点
考虑一下
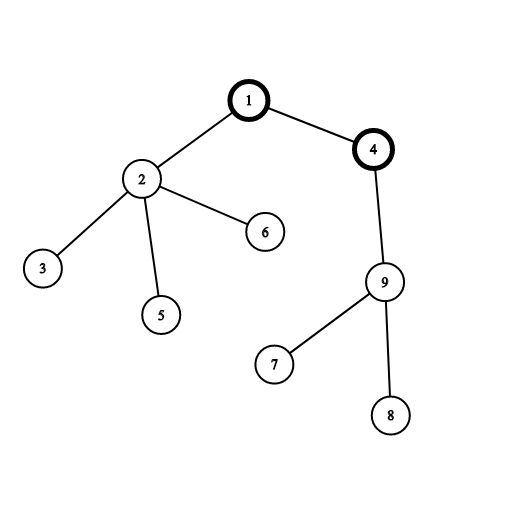
在这张图上 我们将第一个点由1号移动到4的时候
答案会改变的值是 n − s z [ 4 ] − s z [ 4 ] n - sz[4] - sz[4] n−sz[4]−sz[4]
dfs2遍就可以了我怎么菜成了这个样子药丸啊
Codeforces416E. President’s Path
题面描述
我给你一张 n n n( n ≤ 500 n \leq 500 n≤500)的一张图
输出所有点对之间分别的最短路径上的边有多少条
qwq
首先 肥肠套路的一点就是
枚举每条边 看在哪里两个点的最短路径上
O ( n 4 ) O(n^4) O(n4)真的是T飞了。。
然而。。题解真的是牛逼。。完全想不到的哇。。
反正我一开始想的是就像哪几道水题一样最短路套一套就完事了 发现会重复啊。。而且并不会避免。。
其实题解应该就是解决了这个问题
它考虑的是一个点的邻接点所连出去的是否在最短路上
或者说也解决了第一种方法复杂度不对的问题 枚举每个点连出去的边?
对于一个起点 i i i 我们记 c n t [ j ] cnt[j] cnt[j]表示 j j j连出去的边有 c n t [ j ] cnt[j] cnt[j]条是在 i i i到 j j j的最短路上的
那么我们再将 j j j作为 i i i到 k k k的中间节点就行啦~如果这个中间节点的话 那么相应的答案就加上 c n t [ j ] cnt[j] cnt[j]
Codeforces986C. AND Graph
哭哭这题简直就是神仙啊!
题面描述
输入 n , m n,m n,m( 1 ≤ n ≤ 22 1 \leq n \leq 22 1≤n≤22
还有 m m m个数( ≤ 2 n \leq 2^n ≤2n)
如果 a i & a j = 0 a_i \& a_j = 0 ai&aj=0 那么 i , j i,j i,j连边
问最后有多少个联通块
qwq
看到这种题只会 O ( m 2 ) O(m^2) O(m2)啊药丸
感觉做法还是很神仙的qwq
我们考虑输入的 m m m个数分别对应了 ( x , 1 ) (x,1) (x,1),其中 x x x表示值
加入 2 n − 1 2^n - 1 2n−1个点 ( x , 2 ) (x,2) (x,2)
- ( x , 1 ) (x,1) (x,1)可以指向 ( x , 2 ) (x,2) (x,2), ( t o t − x , 2 ) (tot - x, 2) (tot−x,2)指向 ( x , 2 ) (x,2) (x,2)
- ( x , 2 ) (x,2) (x,2)可以指向 ( x ∣ ( 1 < < k ) , 2 ) (x |(1 << k),2) (x∣(1<<k),2) 其中 x x x的第 k k k位上为零
这样就把它们连在一起啦!
我们知道很显然的一个性质 就是如果 x & y = 0 x \& y=0 x&y=0的话
那么 x ∣ ( t o t − y ) = x x | (tot - y) = x x∣(tot−y)=x
那么其实这样构造也就是在满足这个性质
但是点的个数为 O ( 2 n ) O(2^n) O(2n)级别的
所以就对了
Codeforces986F. Oppa Funcan Style Remastered
但是作为Div1最后一题感觉确实不是很难的样子。。
也许难想?
题目描述
反正问题可以转换为
由若干个 k k k的质因数能否组成和为 n n n ( k , n ≤ 1 e 18 k,n \leq 1e18 k,n≤1e18
一共有 q q q ( 1 ≤ q ≤ 10000 ) (1 \leq q \leq 10000) (1≤q≤10000)次询问
其中不同的 k k k最多50个
qwq
首先想到的肯定是质因数分解嘛
但是你会发现…这个要是分的话复杂度显然不对
对此 我们可以采用离线的做法 对相同的 k k k就一起算了
假设 我们分解 k k k可以分解为 p 1 , p 2 . . p m p_1,p_2..p_m p1,p2..pm
-
m = = 0 m == 0 m==0 显然不行
-
m = = 1 m==1 m==1就看 n n n % p 1 p_1 p1
-
m = = 2 m ==2 m==2 其实就相当于求解 a ∗ p 1 + b ∗ p 2 = n a*p_1+b*p_2=n a∗p1+b∗p2=n 其中 b b b的最小合理解为 n p 2 \dfrac{n}{p_2} p2n在膜 p 1 p_1 p1的意义下
那么我们就只需判断 b ∗ p 2 b * p_2 b∗p2是否大于 n n n啦
-
m = = 3 m==3 m==3时 最小的质因数 p 1 p_1 p1显然是小于 100000 100000 100000的
那么我们就在膜 p 1 p_1 p1的意义下去做 其实也就是跑个最短路
记 f [ x ] f[x] f[x]表示到达 x x x所需要的和
即只需要判断 f [ n f[n f[n% p 1 ] p_1] p1]是否大于 n n n就行了( f [ n f[n f[n% p 1 ] p_1] p1]就代表了和 n n n同余的数所需要的,那么剩下的就用 p 1 p_1 p1来补就行了
剩下的就是玄学卡卡卡
Codeforces986E. Prince’s Problem
一道不是很难的题?
大概题解什么的把这道题给写烦了。。或者说我没看懂题解什么意思
题面描述
给你一颗 n ( 1 ≤ n ≤ 1 e 5 ) n(1 \leq n \leq 1e5) n(1≤n≤1e5)个节点的树 每个节点有一个权值 w i ( 1 ≤ w i ≤ 1 e 7 ) w_i(1\leq w_i \leq 1e7) wi(1≤wi≤1e7)
有 q ( 1 ≤ q ≤ 1 e 5 ) q(1 \leq q \leq 1e5) q(1≤q≤1e5)次询问 每次询问 x , y , z ( 1 ≤ x , y ≤ n , 1 ≤ z ≤ 1 e 7 ) x,y,z(1\leq x,y \leq n,1 \leq z \leq 1e7) x,y,z(1≤x,y≤n,1≤z≤1e7) 问 x − > y x->y x−>y的最短路径上的每个点和 x x x的最大公因数的乘积
qwq
我们可以考虑每个质因子对答案的贡献
可以按照质因子而构建很多颗虚树
有一个很显然的性质
- 我们将 x − > y x->y x−>y的答案记为 d ( x , y ) d(x, y) d(x,y)
那么 d ( x , y ) = d ( 1 , x ) ∗ d ( 1 , y ) ∗ d ( 1 , l c a ( x , y ) ) − 1 ∗ d ( 1 , f [ l c a ( x , y ) ] ) − 1 d(x,y) = d(1,x) * d(1,y) * d(1,lca(x,y))^{-1} * d(1,f[lca(x,y)])^{-1} d(x,y)=d(1,x)∗d(1,y)∗d(1,lca(x,y))−1∗d(1,f[lca(x,y)])−1
既然这样
我们就可以离线做了
把所有要求的东西求出来就可以啦!
按照dfs遍历所有点
遍历到一个点 就把这个点的贡献记录上去
那么该点的子树中的所有点都会受到这个点的影响
回溯出去了 就将该点的答案去除即可
如何记录贡献呢?
我们知道 对于一个质因子 p p p的贡献
如果两个数可以表示为 p i ∗ m p^i*m pi∗m, p j ∗ t p^j*t pj∗t
那么贡献即为 p m i n ( i , j ) p^{min(i,j)} pmin(i,j)
观察一下下面的代码 感觉还是肥肠巧妙的!(感觉真的是一点数据结构都没有用呢~
for(int i = w[u]; i > 1; ) {
for(int t = pr[i], j = t; i % t == 0; i /= t, j *= t) {
Mul(s[j], t);
}
}
int len = g[u].size();
for(int k = 0; k < len; ++k) {
for(int i = val[g[u][k].id]; i > 1; ) {
for(int t = pr[i], j = t; i % t == 0; i /= t, j *= t) {
if(g[u][k].v) Mul(d[g[u][k].id], rev(s[j]));
else Mul(d[g[u][k].id], s[j]);
}
}
}
Codeforces986D. Perfect Encoding
题面描述
给出 n n n( 1 ≤ l e n ( n ) ≤ 1.5 e 6 ) 1 \leq len(n) \leq 1.5e6) 1≤len(n)≤1.5e6)
这个 n n n是某个 a [ ] a[] a[]的乘积
让你找到这样一个数组 b b b 使得 a [ i ] ≤ b [ i ] a[i] \leq b[i] a[i]≤b[i]
输出 b [ ] b[] b[]的最小总和
qwq
实际上 b [ ] b[] b[]的乘积必定大于 n n n
我们考虑要最小化总和 s s s
那肯定是将 s s s化成一些相同的数字
即 a n s = ( s x ) x ans = (\dfrac{s}{x})^{x} ans=(xs)x
两边取对数
l n a n s = l n ( s x ) x ln{ans} = ln{(\dfrac{s}{x})^{x}} lnans=ln(xs)x
对右边求导得到 l n n x − 1 ln\dfrac{n}{x} - 1 lnxn−1
当 n x = e \dfrac{n}{x}=e xn=e时取到最大值
所以尽量由3组成 少部分用2去补
3 x = n 3^x= n 3x=n -> x = l o g 3 n x = log_3n x=log3n -> l o g 3 n < 1 0 l e n log_3n <10^{len} log3n<10len-> x < l e n ∗ l o g 3 10 x < len*log_310 x<len∗log310
在一定范围内枚举即可
由于涉及到大整数乘法 而且乘方次数比较高
可以采用FFT + 快速幂
可以采取压位减少复杂度