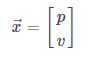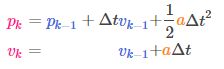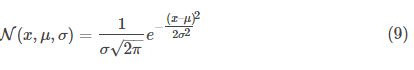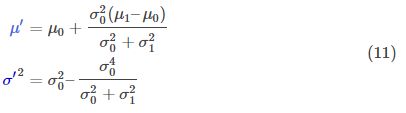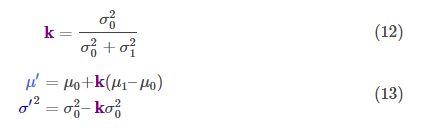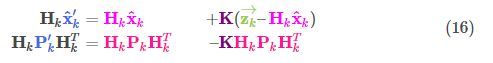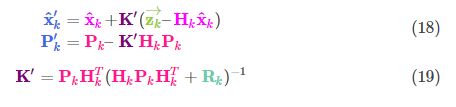卡尔曼滤波学习--外文翻译How a Kalman filter works in pictures
原文地址:http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
课程老师推荐的卡尔曼讲解,翻译了部分内容。均为个人理解,翻译水平不高。
文章讲解基于一个参量为位置和速度的小机器人问题。翻译从How a Kalman filter sees your problem开始
如何用卡尔曼滤波表示你的问题?
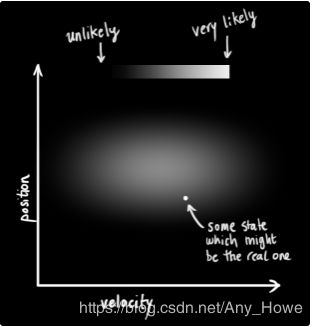
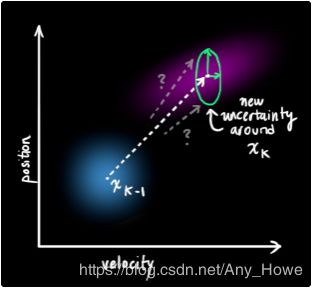
我们来看看我们要阐明的内容。继续用一个只有位置和速度的简单状态进行。
我们不知道实际位置和速度,这两个状态可能的组合有很多种,但是其中一些的可能性比其它情况更大一些。
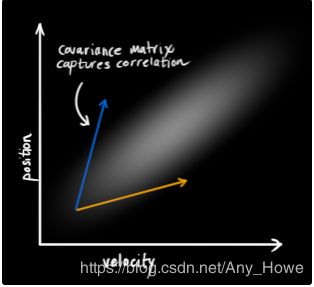
(上图中横轴表示速度,纵轴表示位置,白色区域为可能的状态,越白,可能性越大)
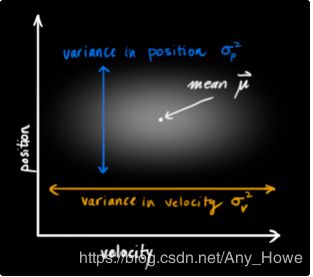
卡尔曼滤波假设所有的变量(本例中是位置和速度)是随机且高斯分布的。每一个变量都有一个均值μ,该值在该变量随机分布的中心(即其最可能的状态),和一个方差σ^2,该值表示不确定性:
在上图中,位置和速度是不相关的,这表示你无法从其中一个变量的状态推算出另一个变量的状态。
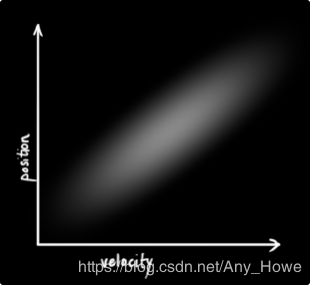
下面这个例子展现了一些更有趣的东西:位置和速度是相关的。你的速度决定了你观测到某一特定位置状态的可能性。
上面这种情况可能会在你需要基于一个旧的位置去估计新位置时出现。如果我们的速度很快,那么我们可能会走的很远,如果很慢,那么我们就不会走的那么远。
记录这种关系非常重要,因为它会给我们更多信息:一次测量告诉我们其他状态参量的可能值。这就是卡尔曼滤波的目标,我们希望从不确定观测中压榨出尽可能多的信息。
这种相互关联可以从协方差矩阵中获得,简单地说,矩阵![]() 中每一个元素表示第i个状态参量和第j个状态参量的相关程度。(你可能可以猜到这个协方差矩阵是对称的,这意味着你交换i,j不会有任何关系)。协方差矩阵常用标签“
中每一个元素表示第i个状态参量和第j个状态参量的相关程度。(你可能可以猜到这个协方差矩阵是对称的,这意味着你交换i,j不会有任何关系)。协方差矩阵常用标签“![]() ”表示,因此其元素表示为“
”表示,因此其元素表示为“![]() ”。
”。
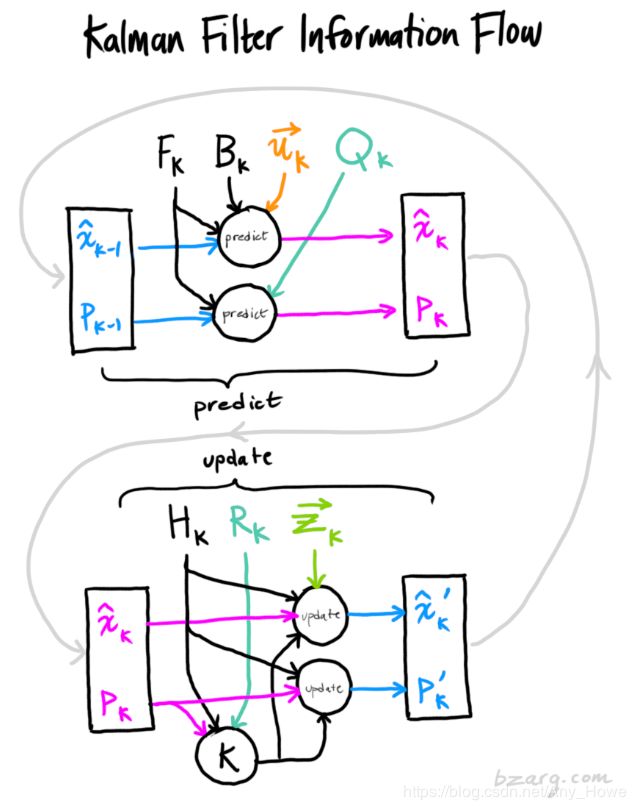
用矩阵表述这个问题
由于我们将已知状态建模成高斯斑点,在时刻k我们需要两条信息:最优估计![]() ,(均值,其他地方称为μ),和它的协方差矩阵
,(均值,其他地方称为μ),和它的协方差矩阵![]()
(当然,我们这里只用了位置和速度,但是记住状态可以使用任意数量的参量,并且代表你想要的任何事物)
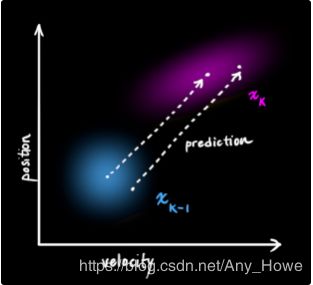
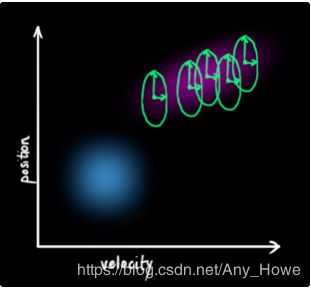
接下来,我们来看看当前状态(current state)(即时刻k-1)并预测下一个时刻k的状态。需要注意,我们不知道哪一个状态是真实的,但是我们的预测函数不关心这个。预测函数对他们都有效,并且会给我们一个新的分布:
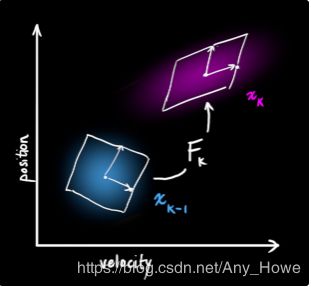
我们用一个矩阵![]() 来表示这个预测步骤:
来表示这个预测步骤:
它采用我们原始估计中的每一点并将其移动到新的预测位置,如果原始估计是正确的,则系统将移动到该位置。
这么来说。我们怎么样用一个矩阵去预测未来下一个时刻的位置和速度呢?从一个非常基础的运动学公式开始:
矩阵表示为:
现在我们就有了一个预测矩阵了,但我们仍然不知道如何更新协方差矩阵。
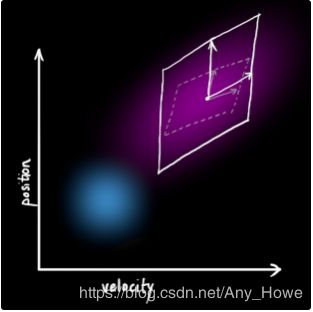
这里我们需要另外一个公式。如果我们用矩阵A乘以分布中的每一个点,协方差矩阵Σ会变成什么样子?
这很简单,我直接给出结果:
因此,将4式与3式结合可以得到:
外部因素
然而,我们并没有获得所有的因素。可能存在一些与状态本身不相关的变化---外部世界会影响这个系统。
例如,如果状态模拟的是火车的运动,火车司机可能会踩油门,导致火车加速。类似的,在我们的机器人例子中,导航系统可能会发出拐弯或者停止的指令。如果我们知道这个世界正在发生什么的一些附加信息,我们就可以用一个向量![]() 来表示,对它进行一些处理,并把它加到我们的预测中作为一个改正。
来表示,对它进行一些处理,并把它加到我们的预测中作为一个改正。
让我们假设我们知道预期的加速度a,因为油门设置或者某条控制指令。从基本的运动学公式,我们有:
矩阵表示为:
![]() 成为控制矩阵,
成为控制矩阵,![]() 表示控制向量。(对于非常简单的没有外部因素影响的系统,可以忽略这两项)
表示控制向量。(对于非常简单的没有外部因素影响的系统,可以忽略这两项)
再加一个细节,如果我们的预测不是出于一个百分百准确的模型呢?
外部不确定性
如果状态根据自己的属性发展,那么一切都很好。只要我们知道外部因素是什么,受外部因素影响的状态仍然发展的会不错。
但是如果有我们不知道的外部因素存在呢?比如,如果我们在跟踪一个四轴飞行器,它可能会受到风的冲击。如果我们在跟踪一个轮式机器人,他可能轮子会打滑,会撞到地面使得速度降低。我们无法跟踪所有这些因素,并且如果发生了这些事情,我们的预测就会偏离,因为我们没有说明这些额外的影响。
我们可以通过在每一步预测中加入新的不确定性,对和“世界”相关的不确定性进行建模(即我们没有记录的东西)
我们最开始估计的每一个状态都可以移到一系列的状态上。由于我们习惯使用高斯斑点,可以说在状态![]() 中的每一个点都被移动到一个协方差为
中的每一个点都被移动到一个协方差为![]() 的高斯斑点中。换一种说法就是,我们将未跟踪的影响作为具有协方差Qk的噪声处理。
的高斯斑点中。换一种说法就是,我们将未跟踪的影响作为具有协方差Qk的噪声处理。
这产生了一个新的高斯斑点,它具有不同的协方差,但是具有相同的均值。
我们需要给协方差阵加上一个![]() 来进行扩展。给出我们完整的预测步骤的表达:
来进行扩展。给出我们完整的预测步骤的表达:
换句话说就是,新的最优估计是从前一最优估计加上一个已知的外部因素校正预测得到的。
新的不确定性是由旧的不确定性加上一些附加的环境不确定性得到的。
这样,我们由![]() 和
和![]() 就对系统位置就有了一个模糊的估计。如果我们从传感器获得了一些数据该怎么做?
就对系统位置就有了一个模糊的估计。如果我们从传感器获得了一些数据该怎么做?
用测量改善估计
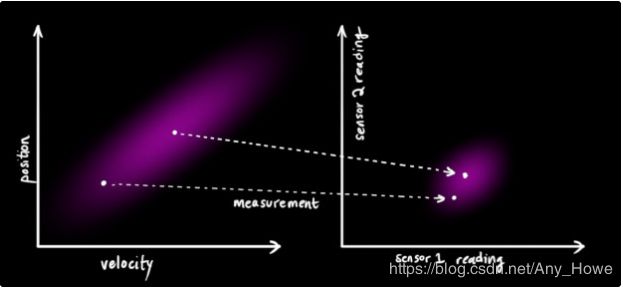
我们可能有一些传感器可以告诉我们系统的一些状态。它们测量什么暂时无关紧要;可能一个获得位置,另一个获得速度。每一个传感器都间接告诉我们状态信息。就是说,传感器对某种状态进行操作,并给出一组读数。
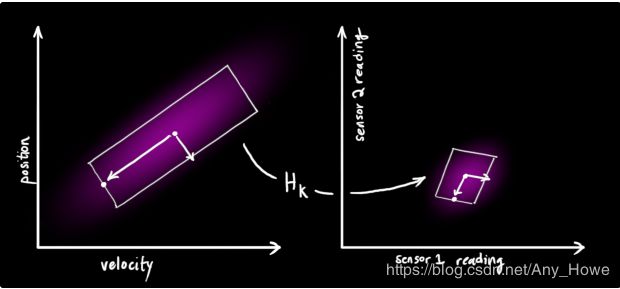
注意到我们传感器用的单位或者尺度会和我们状态使用的不同。你可能猜到了我们接下来要干什么,我们要用一个矩阵![]() 对传感器进行建模。
对传感器进行建模。
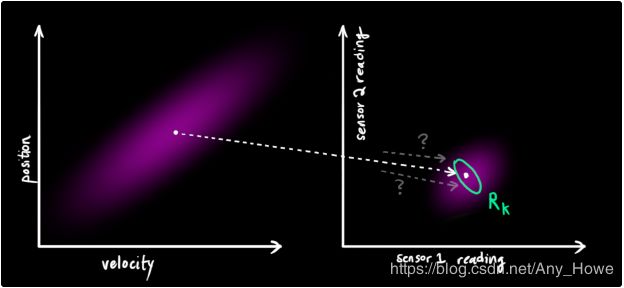
我们用一个常见的方式表示传感器读数的分布:
卡尔曼滤波对处理传感器噪声非常有效。这是说,我们的传感器在某种程度上并不可靠,并且我们最初估计的每一个状态都可能导致传感器读数出现在一定范围。
从我们观测的每一个读数,我们可以猜到系统处于某一种状态。但是由于不确定性的存在,一些状态会比另外一些状态更有可能造成我们看到的读数。
我们用![]() 表示这种不确定性的方差(比如传感器噪声)这个分布的均值等于我们看到的读数,用
表示这种不确定性的方差(比如传感器噪声)这个分布的均值等于我们看到的读数,用![]() 表示这个均值。
表示这个均值。
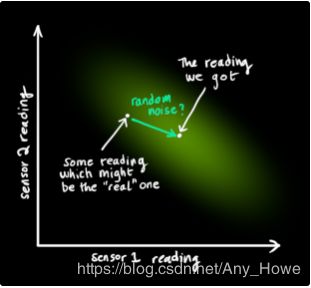
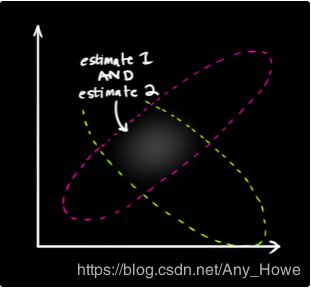
现在我们有两个高斯斑点:一个围绕在我们转换后预测的均值周围,一个在我们实际获得传感器读数周围。
我们必须尝试将基于预测状态(粉红色)的猜测与基于实际观察到的传感器读数(绿色)的不同猜测协调起来。
那么我们新的最可能的状态是什么样子?对于任何可能的读数(![]() ,
,![]() ),我们由两个对应的可能性:(1)传感器读数
),我们由两个对应的可能性:(1)传感器读数
![]() 可能是(
可能是(![]() ,
,![]() )的一个(错误)测量。(2)之前的预测认为(
)的一个(错误)测量。(2)之前的预测认为(![]() ,
,![]() )是我们应该看到的读数。
)是我们应该看到的读数。
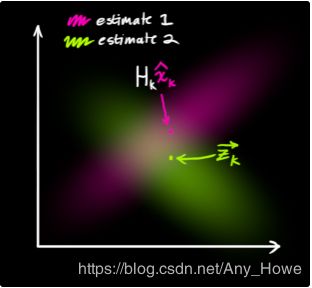
如果我们有这两种概率,并且我们想知道它们都正确的可能性,只需要将它们相乘,所以,我们把这两个高斯斑点相乘:
这样做之后剩下的就是重叠区域,该区域表示两个斑点都可能的情况。这比我们之前的任何一个估计都准确。
这种分布的平均值是两种估计都最有可能出现的情况,也因此,是在已知的所有信息下,对真实构型的最好猜测。
这个看上去像另一个高斯斑点。
这表明,当你把两个有独立均值和方差的高斯斑点相乘,你就可以获得一个新的有自己均值和协方差矩阵的高斯斑点,或许你可以看出这意味着什么:我们可以通过一个公式从旧的参数中获得新的参数!
结合高斯函数
下面来找这个公式。最简单的是先看一维情况。一个一维的均值为μ,方差为![]() 高斯曲线由下式定义:
高斯曲线由下式定义:
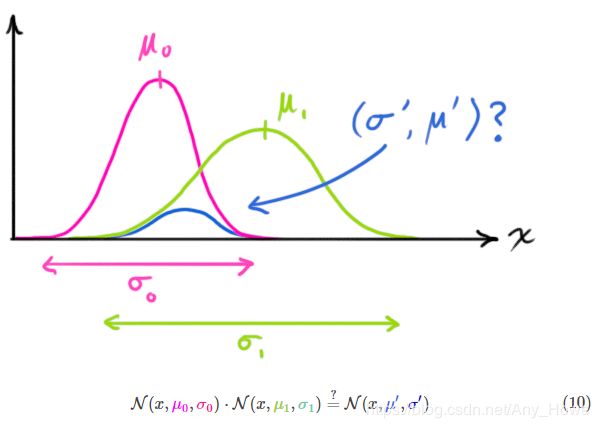
我们想知道当两个高斯曲线相乘的时候可以得到什么。蓝色曲线表示(未归一化)两个高斯曲线的交集。
你可以把方程(9)代入方程(10)做一些代数运算(归一化需要格外注意,这样总概率才是1):
我们可以提出一块并令其为k
请注意如何使用您以前的估计,并添加一些内容来进行新的估计。
那么对于矩阵形式又该怎么办?把式12和13用矩阵形式重写一遍。若![]() 表示一个高斯斑点的协方差阵,
表示一个高斯斑点的协方差阵,![]() 表示其沿各轴的均值,则有:
表示其沿各轴的均值,则有:
K为一个矩阵,表示卡尔曼增益,一会儿就要用到。
全都融合在一起
现在我们有两个分布:预测的测量,![]() 和观测的测量值,
和观测的测量值,![]()
把这些带入到式15可得:
由式14可得卡尔曼增益为:
我们可以在式16和17中消去一个![]() (注意在K中存在一个)。17式中还可以消去一个
(注意在K中存在一个)。17式中还可以消去一个![]() ,得到:
,得到:
这就得到了完整的更新步骤。
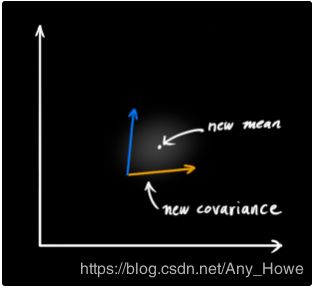
完成了!![]() 就是我们的最新的最优估计。我们可以接着把它和
就是我们的最新的最优估计。我们可以接着把它和![]() 一起反馈给下一轮的预测和更新。
一起反馈给下一轮的预测和更新。
至此,线性系统卡尔曼滤波讲完,原作者将来会将非线性系统的扩展卡尔曼滤波。