Feistel网络结构与DES加密算法的框架简单分析
通常我们耳熟能详的几种加密算法:
对称密钥/私钥密钥:DES、RC6、AES(Rijndael)
非对称秘钥/公钥密钥:RSA
单向散列函数:MD5、SHA
对于对称密钥与非对称秘钥加密算法来说,其区别在于加密密钥与解密秘钥。若加密秘钥与解密秘钥相同或可互相推导/推算则为对称密钥(单钥密钥或私钥密钥),大多数对称密码算法的加密密钥与解密密钥相同;不同且不可互相推导,则为非对称秘钥(双钥密钥或公钥密钥)。由于加密秘钥与解密密钥相同,所以其结构就简单的多。以Feistel结构来说其加密解密流程结构基本相同,而依据Feistel结构作为基本结构的有DES、RC6、MARS等加密算法。
我们知道一个加密结果的好坏不仅取决于其加密密算法的好坏(逻辑严谨性、效率等),还取决于其密钥长度。由于DES的密钥长度有效位为56bit(实际64bit,另外8bit是每个字节的校验位),所以其密钥空间(数量)为N=2^56,对于现今的计算机CPU频率来说,若采用暴力破解的方法来破解一个DES加密密文是不在话下的,并且3DES的产生与AES的产生都对DES有了完全替代的趋势。但是对于研究Feistel网络结构来说,DES仍是最重要的一种加密算法。所以研究Feistel网络结构一个重要的研究问题就是DES的基本加密流程。
1、Feistel网络结构加密解密流程:
round称为轮,是加密的一个独立的步骤,整个加密就是对同一步骤进行多次循环(DES选择的是16轮循环)。轮数越多加密的效果越好,当然其加密时间也就越长。
其特性参数:
①明文(输入)块大小(Block Size):64bit~128bit,且是2的倍数;
②密钥长度/大小(Key Size):56~256
③Number of Rounds:循环次数
④Round Function:轮函数,一定是非线性的,不要求可逆
我们拿出单独的一轮(第一轮Round1)来看其一轮的加密流程:
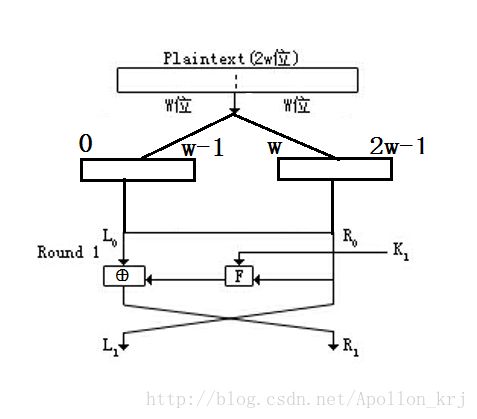
明文(Plaintext)长度为2W位(该结构加密的名文bit数长度必须为偶数,比如DES的明文长度为64bit)。
①先将2w位的明文分为左半部分(前w位L0)和右半部分(后w位R0)。
②将输入的右侧R0,直接输出到输出的左侧为密文的左半部分L1。
③将输入的右侧R0与子密钥K1进行F函数操作(K1和R0作为自变量)得到运算结果,即Output_1 = F(K1,R0)。
④将经过F函数运算的结果Output_1与L0进行异或操作,得到结果作为密文的右半部分R1。
⑤第一轮Round1的密文作为第二轮Round2的明文进行相同步骤的加密操作,循环操作。
注意:最后一轮的结果在基本流程上(基本流程为下图所示)要再交换左右两部分(参照第一幅图)。以保证加密与解密的结构相同。
一个基本的加密其轮流程如下所示:

基本轮流程中,第i轮的输入输出分别为:
输入:
Li-1 = Ri-2
Ri-1 = (Li-2)⊕F(Ri-2,Ki-1)
输出:
Li = Ri-1 = (Li-2)⊕F(Ri-2,Ki-1)
Ri =(Li-1) ⊕ F(Ri-1,Ki) = (Ri-2) ⊕ F( [(Li-2)⊕F(Ri-2, Ki-1)], Ki)
很明显这是一个迭代的过程。
两个注意点:
①第一轮的左右两部分输入是由原有2W长度的信息等分而来,其它轮的左右输入是由上一步输出得来。
②最后一轮的输出在输出以后需要进行一次左右交换,已达到加密解密同流程的目的。
Feistel网络结构有一个特点,就是加密与解密流程是完全相同的。也就是加密解密算法相同,不同的只是初始输入值与子密钥的使用顺序(即所谓加密解密对称性)。

密钥使用:
加密时为:K1->K2->K3->…->Ki->…->Kn
解密时为:Kn->…->Ki->…->K3->K2->K1
输入输出:
加密时:输入明文,输出密文
解密时:输入密文,输出明文
2、Feistel网络结构的F函数:
对于Feistel网络结构,其加密核心在与F函数的选定,不同的F函数就是遵循Feistel结构的不同的加密算法(如DES),一个好的F函数对于加密效果至关重要,一般情况下,F函数需要满足以下几点:
①不要求可逆:即不求F函数有反函数
②非线性;
③混乱性;
④扩散性;
⑤雪崩性:即随着轮数增加其加密效果雪崩式增强;
⑥比特独立性:一个bit的加密结果不依赖于其他bit。
3、DES算法中的F函数:
DES加密算法作为Feistel网络结构的一种应用,其F函数结构如下所示(绿色线内即DES的F函数流程):

F函数的基本操作流程为:
(1)、将64bit的明文右半部分即32bit扩展为48bit:采用的是4个bit一组,分为8组,每一组前后各加1bit(增加的bit数=2*1*8=16bit)。其增加按照下表进行(虚线以外的为增加的bit所在位置,如:第一组前是32,即在第一组前加一个bit为整个右半部分的32bit的第32位的bit值{0,1}):

用更加清晰地一张图来体现:
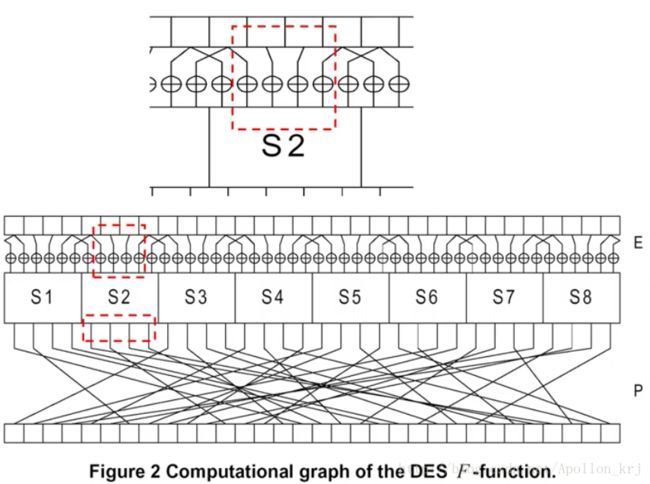
比如:原本的名文右半部分32bit为:
0101
1010
1001
1100
1010
0110
1001
1010
经过扩充以后为:
0 0101 1
1 1010 1
0 1001 1
1 1100 1
0 1010 0
0 0110 1
0 1001 1
1 1010 0
(2)、得到的48bit扩充信息,和子密钥Ki进行异或操作,得到48bit的结果;
(3)、将扩充信息和子密钥异或后的结果进行压缩(48bit压缩到32bit),压缩的方式是经过S盒(4*16的矩阵)进行替换,S盒函数是经过严格计算获得的,其S1盒的替换表与流程如下所示:

一个组6bit,共8组(6bit*8=48bit),即有8个S盒,每个S盒是固定的但是都是不相同的。拿S1盒来说:B1B2B3B4B5B6,第一个比特和最后一个比特,即B1B6确定表中的行数(B1B6=00、01、10、11分别为0、1、2、3);每一组的中间四个比特确定列数(B1B2B3B4=0000~1111即0~15列)。
eg:B1B2B3B4B5B6=101011。则B1B6=11(3)确定最后一行,B2B3B4B5=0101(5)确定第5列。3行5列即值为9(1001),所以101011的6bit经过压缩后的4bit为1001。这个替换的过程比较简单,但是其核心S盒的设计是充满了数学与密码学智慧的。美国当初公布DES算法时没有提出为什么选择这样一个表来压缩,只是给出了S盒的内容与使用。但是1976年NSA(NationalSecurityAgency)提出了S盒设计的几条原则,基本内容如下:

S盒的实现就像一个编码器,只不过是6-4线的。而不是8-3线或者16-4线的。更准确来说是一个索引表,原来的6bit作为索引,转换为索引到的4bit。
S盒的设计原则是遵循了F函数的要求来设计的,比如非线性、雪崩性、比特统计独立性等。对于S盒的分析,这里不进行研究,感兴趣的朋友可以百度S盒的设计准则与分析,或参考:DES中S盒设计准则的分析
(4)、置换运算P(经过一个P盒进行置换):指的是将32bit压缩后的信息进行bit置换操作,改换位操作目的是打乱其原有排序规律(F函数的混乱性原则)。P盒与S盒的硬件设计规律如下图所示(P盒是打乱原有01序列,S盒是译码器+P盒+编码器构成的(以8-3线为例)):
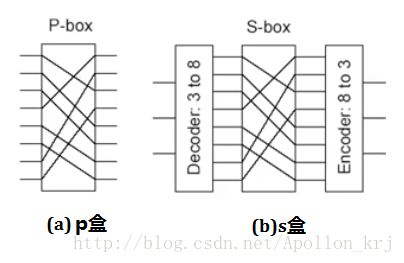
而关于DES的F函数中的P盒设计,这里也不做研究,仅仅是了解学习一下DES的F函数的流程而已(DES中不仅F函数中有P盒存在,子密钥的产生过程中也存在P盒,关于子密钥的产生我们在以后的DES算法具体剖析中再来分析)。
经过以上四步,就完成了DES加密中重要的F函数的操作,经过分析我们发现,F函数的基本流程并不复杂,其复杂点(或者说算法精要)是32bit扩充48bit的思想、S盒设计思想、P盒设计。对于这些问题的分析与设计是需要丰富的密码学经验的,并且由严谨的数学、逻辑学推导。或许有人怀疑S盒的设计中存在“后门”,但就目前来看这一猜想是不成立的。
3、设计简单的F函数测试加密解密过程:
由于DES的F函数过于复杂,且明文与密钥长度过长,不便进行测试,所以,我们自行设计一个F函数:
F(Ri-1,Ki)=(Ri-1)⊕(Ki)
明文块长度(Block Size)为8bit,子密钥长度为4bit,要加密的信息是1100 0010。
假设K1=1111,K2=1110共进行两轮加密。
(1)、加密:
明文:1100 0010作为最初输入 —>L0 = 1100,R0 = 0010
Round 1:
K1 = 1111
L1 = R0 = 0010
R1 = L0⊕F(R0,K1)=L0⊕(R0⊕K1)=1100⊕(0010⊕1111)=1100⊕1101=0001
Round 2:
K2 = 1110
L2 = R1= 0001
R2 = L1⊕F(R1,K2)=L1⊕(R1⊕K2)=0010⊕(0001⊕1110)=0010⊕1111=1101
最后一轮L2、R2交换:
加密完成后的密文:1101 0001(与加密前明文相同)
(2)、解密:
密文:1101 0001最初作为输入 —> L0 = 1101,R0=0001
Round 1:
K2 = 1110
L1 = R0 = 0001
R1 = L0⊕F(R0,K2)=L0⊕(R0⊕K2)=1101⊕(0001⊕1110)=1101⊕1111=0010
Round 2:
K1 = 1111
L2 = R1= 0010
R2 = L1⊕F(R1,K1)=L1⊕(R1⊕K1)=0001⊕(0010⊕1111)=0001⊕1101=1100
最后一轮L2、R2交换:
解密完成后的明文:1100 0010
用该简单的例子,验证了加密解密用同一个流程的可行性。这也是Feistel网络结构的一个十分重要的特性,不必为解密单独再实现软件/硬件,而AES(Rijndael)算法的加密解密流程就不同(是相反的),需要单独实现解密软件、硬件。并且我们发现在DES的加密操作中位运算比较多,用硬件实现DES比软件实现似乎效率更高,加密速度更快。
视频学习资源来源:(信息安全概论-中国农业大学-吕春利)http://www.icourse163.org/course/CAU-251001#/info
个人推荐图书资源:
(1)、《应用密码学–协议算法与C源程序》[美]Bruce Schneier著 ,机械工业出版社。
(2)、《图解密码技术》[日]结城浩著,人民邮电出版社
