A.pro读算法の7：快速搞定bfs算法

bfs算法，即广度优先算法(Breadth First Search)。

和dfs类似的，同样可以遍历一张图。它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。和dfs一样，这是一种蛮力的解决方案。

比如，你的眼镜掉了，你趴在地上找。你会先伸手找离你最近的地方，如果没有，再向远处寻找...

和深搜的区别是：同样是对四周进行扩展，只是bfs是所有能扩展的点进入队列，不像深搜，不到最后不回头。

来举个例子。

---

有一个n*n的迷宫，给定入口inx,iny和出口outx,outy，编一个程序输出最短路径的步数。

样例输入:

3 3
001
101
100
1 1 3 3

样例输出:

5

虽然我们之前已经用过dfs来解决它，但是当这个地图过大，那么可能递归函数会爆掉。

简单分析：与dfs不同，dfs的终止条件是到达目的地就退出，结束搜索，当然人家的搜索方法也是决定了第一次到达地步长最短了。因此，bfs同样也是能够找出多条到达目的地的路径，但是第一次到达的时候用的步长一定是最短的。bfs应该是能够想象成一个小圆点不断的向四周膨胀至结束位置的过程。

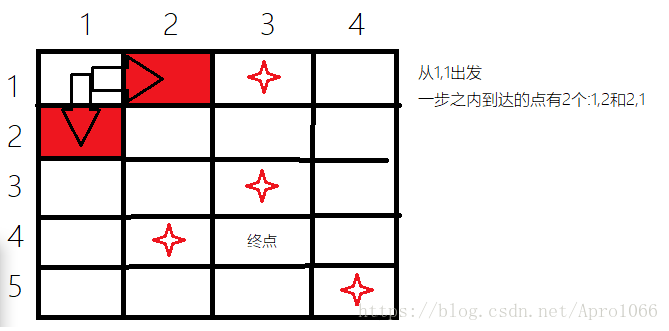
我们这里设inx,iny=(1,1)，然后到达终点(4,3)。

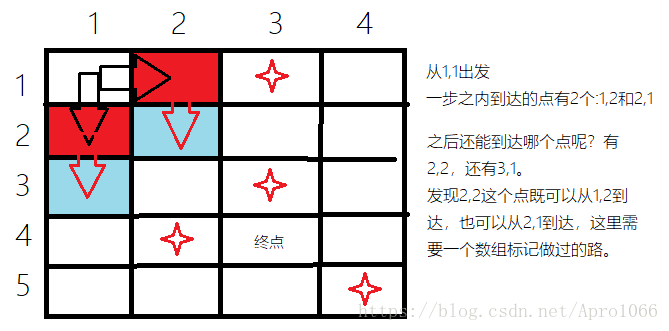
这时2步能走到的点全部走到了，可是还没到终点。没有别的办法，只有继续往下试，就像“你的眼镜掉了，你趴在地上找。你会先伸手找离你最近的地方，如果没有，再向远处寻找...”是一个道理了。我们需要重复刚才的方法，直到走到终点。

回顾刚才的算法，可以用一个队列来模拟这个过程。

    int tox[5]={0,1,0,-1,0};//4个方向 
int toy[5]={0,0,1,0,-1};//哪些坐标已经在队列中了，防止一个点被重复走 
int a[2001][2001];//地图 
int b[2001][2001];
int q[2560001][5];//队列模拟过程
//q[i][1]表示x坐标，q[i][2]表示y坐标
//q[i][3]是路径，本题可以省略 
//q[i][4]为步数 
register int i,j,k,head(1),tail(1);
	int n,inx,iny,outx,outy;
	cin>>n;//n*n的矩阵 
	string s1;
	for(i=1;i<=n;i++)
	{
		cin>>s1;
		for(j=0;j>inx>>iny>>outx>>outy;//输入入口和出口 
	q[head][0]=inx;//第一步inx,iny加入队列 
	q[head][1]=outx;
	q[head][2]=0;
	q[head][3]=0;
	tail++;
	b[inx][iny]=1;

从1,1开始，尝试走到1,2。

int x1=q[head][1];
int y1=q[head][2]+1;

判断1,2是否越界。

if(x1<1 || x1>n || y1<1 || y1>n)
{
    continue;
}

判断1,2是否为障碍物或者已经走过。

if(a[x1][y1]==0 && b[x1][y1]==0)
{
    
}

符合条件？那么坐标1,2入队，并且标记这个点已经走过。

		if(a[x1][y1]==0 && b[x1][y1]==0)//判断当前坐标是否为障碍物或已经走过 
			{
				b[x1][y1]=1;//那么坐标1,2入队，并且标记这个点已经走过。
				//广搜每个点一般只入队一次，和dfs不同，不需要吧b数组还原。 
				q[tail][0]=x1;
				q[tail][1]=y1;
				q[tail][2]=head;
				q[tail][3]=q[head][3]+1;//步数+1 
				tail++;//尾指针向后挪一位 
			}

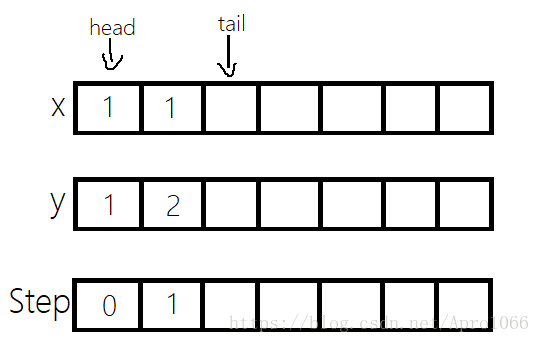
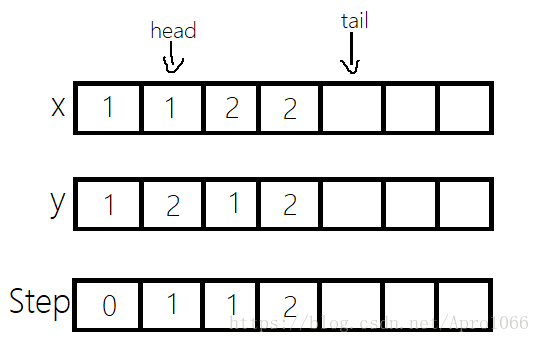
队列的情况如下：

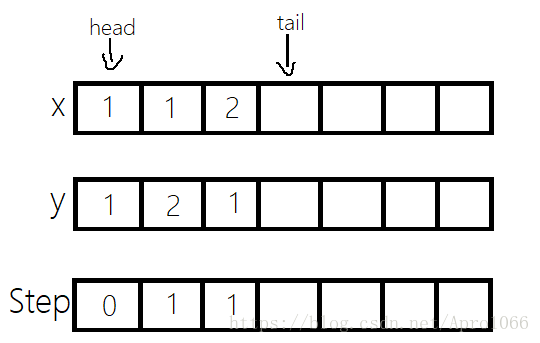
接下来继续尝试往其他方向走。下一步2,1可以从1,1过来，因此2,1也需要入队，代码实现和1,2的操作是一样的。

队列情况：

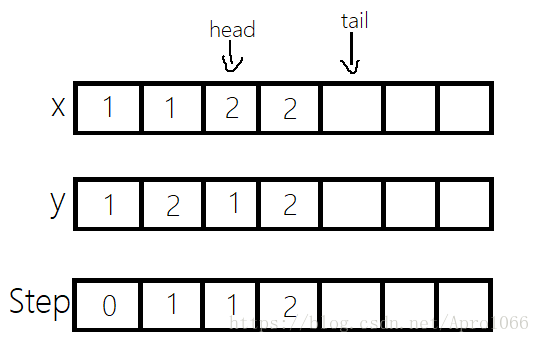
对1,1拓展完毕后，1,1就已经没有用了，所以1,1需要出队。出队的操作非常简单，只需一句话。

head++；

继续。1,1出队后，head现在指向了1,2这个点。所以我们要在这个点继续拓展。从1,2可以到达2,2，将2,2加入队列。

好了,1,2已经拓展完毕，对我们来说没有用了，所以1,2出队。1,2出队后，head指向了2,1这个点。

到目前为止我们已经拓展出2步以内可以到达的所有点，可是依旧没有到达终点，因此还要继续，直到走到终点，算法结束。

完整代码如下。

#include 
#include 
using namespace std;
int tox[5]={0,1,0,-1,0};//4个方向 
int toy[5]={0,0,1,0,-1};//哪些坐标已经在队列中了，防止一个点被重复走 
int a[2001][2001];//地图 
int b[2001][2001];
int q[2560001][5];//队列模拟过程
//q[i][1]表示x坐标，q[i][2]表示y坐标
//q[i][3]是路径，本题可以省略 
//q[i][4]为步数 
int main()
{
	ios::sync_with_stdio(false);
	register int i,j,k,head(1),tail(1);
	int n,inx,iny,outx,outy;
	cin>>n;//n*n的矩阵 
	string s1;
	for(i=1;i<=n;i++)
	{
		cin>>s1;
		for(j=0;j>inx>>iny>>outx>>outy;//输入入口和出口 
	q[head][0]=inx;//第一步inx,iny加入队列 
	q[head][1]=outx;
	q[head][2]=0;
	q[head][3]=0;
	tail++;
	b[inx][iny]=1;//起点已经走过 
	while(headn || y1<1 || y1>n)//如果超过了地图边界 
			{
				continue;
			}
			if(a[x1][y1]==0 && b[x1][y1]==0)//判断当前坐标是否为障碍物或已经走过 
			{
				b[x1][y1]=1;//那么坐标1,2入队，并且标记这个点已经走过。
				//广搜每个点一般只入队一次，和dfs不同，不需要吧b数组还原。 
				q[tail][0]=x1;
				q[tail][1]=y1;
				q[tail][2]=head;//这个点是head拓展而来的，所以他的父级为head，同时这是个路径，本题可以省略。 
				q[tail][3]=q[head][3]+1;//步数+1 
				tail++;//尾指针向后挪一位 
			}
			if(x1==outx && y1==outy)//是否到达终点
			{
				goto loop;//直接跳出 
			}
		}
		head++;//千万不要忘记，如果一个点拓展结束后，head+1才能对下一个点进行拓展 
	}
	loop://跳到这来 
	cout<

广度优先即是要按层数一层一层来遍历，先将一层全部扩展，然后再进行下一层。

过程：

 1.次取出队列首元素（初始状态），进行拓展。

 2.把拓展所得到的可行状态都放到队列里面。

 3.将初始状态删除。

 4.一直进行以上三步直到队列为空。

与dfs的对比

深度优先搜索用栈（stack）来实现，整个过程可以想象成一个倒立的树形：

1、把根节点压入栈中。

2、每次从栈中弹出一个元素，搜索所有在它下一级的元素，把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。

3、找到所要找的元素时结束程序。

4、如果遍历整个树还没有找到，结束程序。

广度优先搜索使用队列（queue）来实现，整个过程也可以看做一个倒立的树形：

1、把根节点放到队列的末尾。

2、每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。

3、找到所要找的元素时结束程序。

4、如果遍历整个树还没有找到，结束程序。

bfs在求解最短路径或者最短步数上有很多的应用，应用最多的是在走迷宫上。（当然dfs也可以做到）

下面是bfs的模版。

inline void bfs()
{
    初始化，初始状态存入队列；
    队列首指针head=0；
    队列尾指针tail=1；    
    while(head