吴恩达机器学习(Machine Learning)课程总结笔记---Week3
文章目录
- 0 概述
- 1. 课程大纲
- 2. 课程内容
- 2.1 逻辑回归假设模型的引入
- 2.1.1 分类问题
- 2.1.2 逻辑回归的假设表示
- 2.1.3 假设函数的决策边界
- 2.2 逻辑回归的求解
- 2.2.1 定义损失函数
- 2.2.2 简化损失函数并使用梯度下降求解
- 2.2.3 高级优化算法
- 2.2.3.1 高级优化算法的优缺点
- 2.2.3.2 使用高级优化算法(fminunc)
- 2.3 多分类问题
- 2.3.1 One-vs-all
- 2.4 正则化引入
- 2.4.1 欠拟合(under fitting)和过拟合(over fitting)
- 2.4.2 怎么解决过拟合问题
- 2.4.3 正则化的costFunction
- 2.4.4 线性回归的正则化
- 2.4.4.1 梯度下降方法
- 2.4.4.2 正规方程法
- 2.4.5 逻辑回归的正则化
- 3. 课后编程作业
- 4. 总结
0 概述
前两周,我们通过房价预测引入了单变量和多变量线性回归,而后又了解了一下非线性回归,归根结底它们都属于回归问题。而实际生活中还有一类问题需要我们来预测,那就是分类问题。
本周学习如何使用逻辑回归(logistic regression)来完成分类问题的预测。
至此监督学习的两大类问题,就齐备了。
1. 课程大纲
2. 课程内容
2.1 逻辑回归假设模型的引入
2.1.1 分类问题
如下图所示,即是分类问题

可以看出分类问题,多数情况是二元分类(是/不是)。
1. 当然也存在元分类{1, 2, 3, 4},后续会提到,我们同样使用二元分类可以解决。
2. 极限情况,当分类的类别足够多的时候,实际上就转化为了回归问题。
我们可以尝试用线性回归函数 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn解决此问题,设定一个阈值 t h r e s h o l d = 0.5 threshold = 0.5 threshold=0.5:
if h θ ( x ) ≥ 0.5 → y = 1 h_{\theta}(x) \geq 0.5 \rightarrow y=1 hθ(x)≥0.5→y=1
if h θ ( x ) < 0.5 → y = 0 h_{\theta}(x) < 0.5 \rightarrow y=0 hθ(x)<0.5→y=0
但是线性回归有两个问题
(1) 线性回归的值,可能远大于1或者远小于0,这样预测1和0很奇怪
(2) 一旦引入新的样本,很容易就会破坏线性回归的预测,如下图
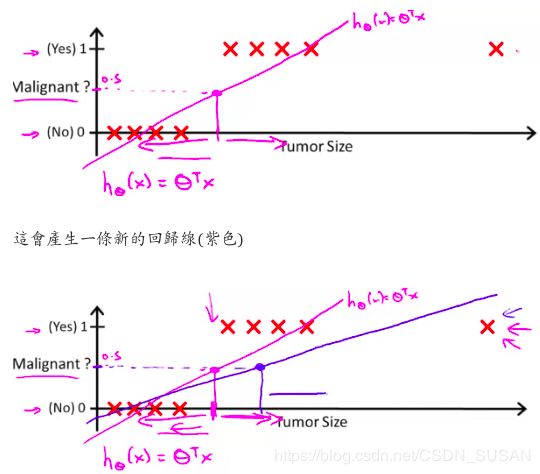
引入新的样本之后,阈值分类点发生了变化,导致了分类错误。
基于以上两点,我们不能使用线性回归来解决分类问题,我们需要找到一个满足假设函数 h θ ( x ) h_{\theta}(x) hθ(x),满足其值永远在[0, 1]之间,因此就引入了逻辑回归。
2.1.2 逻辑回归的假设表示
引入s形函数(sigmoid), g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1,其曲线图如下图所示:
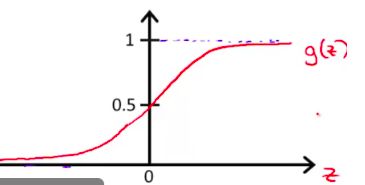
可以看到sigmoid函数的值域在[0, 1]之间。
因此我们定义逻辑回归的假设函数位 h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta T_{x}}} hθ(x)=g(θTx)=1+e−θTx1,此时 h θ ( x ) h_{\theta}(x) hθ(x)的值表示预测为正类别( y = 1 y=1 y=1)的概率。
用条件概率表示如下:
h θ ( x ) = P ( y = 1 ∣ x ; θ ) = 1 − P ( y = 0 ∣ x ; θ ) h_{\theta}(x)=P(y=1 | x ; \theta)=1-P(y=0 | x ; \theta) hθ(x)=P(y=1∣x;θ)=1−P(y=0∣x;θ)
2.1.3 假设函数的决策边界
对于假设函数 h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta T_{x}}} hθ(x)=g(θTx)=1+e−θTx1,我们假定概率大于0.5为正类,概率小于0.5位反类,则可推导 y = 1 → h θ ( x ) ≥ 0.5 → θ T x ≥ 0 y=1 \rightarrow h_{\theta}(x) \geq 0.5 \rightarrow \theta^{T} x \geq 0 y=1→hθ(x)≥0.5→θTx≥0,则
θ T x ≥ 0 \theta^{T} x \geq 0 θTx≥0就是决策边界。
(1) 线性决策边界
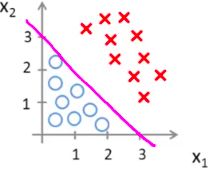
θ T x = − 3 + x 1 + x 2 ≥ 0 \theta^{T} x = -3+x_{1}+x_{2} \geq 0 θTx=−3+x1+x2≥0
(2) 非线性决策边界
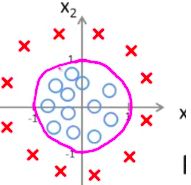
θ T x = − 1 + x 1 2 + x 2 2 ≥ 0 \theta^{T} x = -1+x_{1}^{2}+x_{2}^{2} \geq 0 θTx=−1+x12+x22≥0
2.2 逻辑回归的求解
2.2.1 定义损失函数
回忆线性回归的损失函数为: J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \frac{1}{2}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ)=m1∑i=1m21(hθ(x(i))−y(i))2
逻辑回归是否能够继续使用呢?答案是不行的
因为这个损失函数,sigmoid平方项将会造成一个非凸的函数图形。
如下图所示:
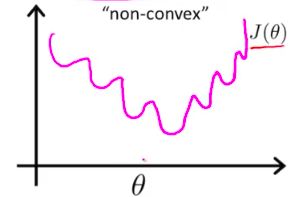
这个损失函数,无法通过梯度下降法得到全局最优解。
因此重新定义逻辑回归的损失函数如下:
cost ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 \operatorname{cost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{cc}{-\log \left(h_{\theta}(x)\right)} & {\text { if } y=1} \\ {-\log \left(1-h_{\theta}(x)\right)} & {\text { if } y=0}\end{array}\right. cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x)) if y=1 if y=0
这个函数的特点就是当预测错误时,预测误差会变大,预测正确时,预测误差会趋近0。
分析当 y = 1 y=1 y=1绘制 − log ( h θ ( x ) ) -\log (\operatorname{h} \theta(\mathrm{x})) −log(hθ(x))如下图:

可以看到, h θ x h_\theta{x} hθx 越接近1, − log ( h θ ( x ) ) -\log (\operatorname{h} \theta(\mathrm{x})) −log(hθ(x))越接近0,反之越接近越无穷大。
因此满足上述特点,对于第二行分析和第一行一样。
2.2.2 简化损失函数并使用梯度下降求解
2.2.1节中,我们定义了损失函数如下:
cost ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 \operatorname{cost}\left(h_{\theta}(x), y\right)=\left\{\begin{array}{cc}{-\log \left(h_{\theta}(x)\right)} & {\text { if } y=1} \\ {-\log \left(1-h_{\theta}(x)\right)} & {\text { if } y=0}\end{array}\right. cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x)) if y=1 if y=0
但是,它明显是一个分段函数,我们在计算误差的时候如果每次都要对 y y y进行判断,显然无法使用梯度下降法求解。
因此需要将其统一处理,得到简化的损失函数为:
cost ( h θ ( x ) , y ) = − y log ( h θ ( x ) ) − ( 1 − y ) log ( 1 − h θ ( x ) ) \operatorname{cost}\left(h_{\theta}(x), y\right)=-y \log \left(h_{\theta}(x)\right)-(1-y) \log \left(1-h_{\theta}(x)\right) cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
对所有样本的损失函数即为:
J ( θ ) = 1 m ∑ i = 1 m cost ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m [ ∑ i = 1 m y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] \begin{aligned} J(\theta) &=\frac{1}{m} \sum_{i=1}^{m} \operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) \\ &=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] \end{aligned} J(θ)=m1i=1∑mcost(hθ(x(i)),y(i))=−m1[i=1∑my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
使用梯度下降法不断迭代 θ \theta θ可得:
θ j : = θ j − α ∂ ∂ θ j J ( θ ) = θ j − α ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J(\theta)=\theta_{j}-\alpha \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj:=θj−α∂θj∂J(θ)=θj−α∑i=1m(hθ(x(i))−y(i))xj(i)
可以发现逻辑回归梯度下降迭代的表达式和线性回归的一模一样,但是由于 h θ ( x ) h_{\theta}(x) hθ(x)的不同,其计算是完全不同的。
向量化表示:
损失函数的向量化定义如下,
h = g ( X Θ ) h=g(X \Theta) h=g(XΘ)
costFunction = F ( Θ ) = 1 m ( − y ⃗ T log ( h ) − ( 1 − y ⃗ ) T log ( 1 − h ) ) =\mathrm{F}(\Theta)=\frac{1}{m}\left(-\vec{y}^{T} \log (h)-(1-\vec{y})^{T} \log (1-h)\right) =F(Θ)=m1(−yTlog(h)−(1−y)Tlog(1−h))
梯度下降计算 Θ \Theta Θ向量形式如下,
Θ : = Θ − α 1 m X T ( g ( X Θ ) − y ⃗ ) \Theta :=\Theta-\alpha \frac{1}{m} X^{T}(g(X \Theta)-\vec{y}) Θ:=Θ−αm1XT(g(XΘ)−y)
2.2.3 高级优化算法
除了梯度下降法,还有很多其他的优化算法:
共轭梯度法,BFGS,L_BFGS
2.2.3.1 高级优化算法的优缺点
优点:不需要手动选择学习率,可以理解为它们有一个智能的内循环(线搜索算法),它会自动尝试不同的学习速率 α \alpha α,并自动选择一个最好的学习速率 α \alpha α ;一般情况下比梯度下降更快收敛。
缺点:更加复杂
2.2.3.2 使用高级优化算法(fminunc)
吴恩达建议我们直接使用前人已经建立好的函数库,没必要造轮子。
fminunc函数的使用,这里就不详述了。具体可参见如下资料:
https://zlearning.netlify.com/communication/matlab/fminunc.html
2.3 多分类问题
一开始我们就提到了多分类问题, y y y{属于1, 2, 3, 4}。当我们学习了二元分类,多酚类问题怎么处理呢?
一个最简单的想法,就是将多分类问题,转化为二元分类问题,这就是one-vs-all方法。
2.3.1 One-vs-all
将要预测的类别处理为一类,其他剩余类别当做第二类。
如下图所示有三个类别:

预测Class 1,我们吧蓝色正方形和红色X作为一类看待
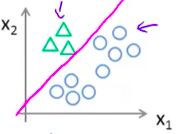
因此根据One-vs-all方法,多分类问题,有多少个类就需要多少个 h θ ( x ) h_\theta(x) hθ(x)。
2.4 正则化引入
2.4.1 欠拟合(under fitting)和过拟合(over fitting)
欠拟合:训练数据中有显著的预测误差,如下图
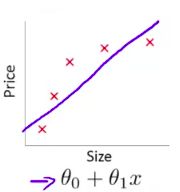
过拟合:训练数据预测误差很小,但是测试数据预测误差很大,如下图
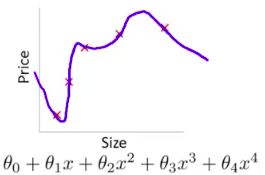
过度追求训练误差,导致泛华能力下降,预测新增数据,带来很大误差。
真正恰当的拟合曲线如下图,
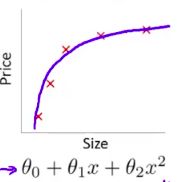
注意:奥卡姆剃刀原则,在达到一定要求的基础上,模型简洁至上。
If we have too many features, the learned hypothesis may fit the training set very well (J(θ)=0), but fail to generalize to new examples(Predictions on new examples)
2.4.2 怎么解决过拟合问题
(1) 降低features的数量:手动选择要保留的特征,哪些变量更为重要,哪些变量应该保留,哪些应该舍弃;使用模型选择算法(稍后在课程中学习),算法会自动选择哪些特征变量保留,哪些舍弃。
(2) 使用正则化:保留所有的特征,但减少参数 θ j \theta_{j} θj 的大小或者减少量级;当有很多个特征的时候,并且每个特征都会对最终预测值产生影响,正则化可以保证运作良好。
2.4.3 正则化的costFunction
正则化的目的是为了简化假设模型,根据奥卡姆剃刀原则,越简单的模型越不容易出现过拟合。
修改costFunction如下:
CostFunction = F ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ i = 1 m θ j 2 ] =\mathrm{F}(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{i=1}^{m} \theta_{j}^{2}\right] =F(θ)=2m1[∑i=1m(hθ(x(i))−y(i))2+λ∑i=1mθj2]
λ ∑ i = 1 m θ j 2 \lambda \sum_{i=1}^{m} \theta_{j}^{2} λ∑i=1mθj2是正则化项,它缩小每个参数的值。 λ \lambda λ 是正则化参数, λ \lambda λ 控制两个不同目标之间的取舍,即更好的去拟合训练集的目标和将参数控制的更小的目标,从而保持假设模型的相对简单,避免出现过拟合的情况。
(1) 选择的 λ \lambda λ 太大:可能会过多地消除特征,导致 θ \theta θ 都约等于 0 了,最终预测函数变成了水平直线了。这就变成了欠拟合的例子了(偏见性太强,偏差过高)。
(2) 选择的 λ \lambda λ 太小:失去了正则项的意义。
2.4.4 线性回归的正则化
2.4.4.1 梯度下降方法
假设函数:
h θ ( x ) = θ T x = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_{\theta}(x)=\theta^{T} x=\theta_{0} x_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} hθ(x)=θTx=θ0x0+θ1x1+θ2x2+⋯+θnxn
损失函数:
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right] J(θ)=2m1[∑i=1m(hθ(x(i))−y(i))2+λ∑j=1nθj2]
迭代函数:
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j} :=\theta_{j}\left(1-\alpha \frac{\lambda}{m}\right)-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj:=θj(1−αmλ)−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
这里 ( 1 − α λ m ) \left(1-\alpha \frac{\lambda}{m}\right) (1−αmλ)会恒小于1,比如0.99。于是梯度下降的过程就是每次更新都把参数乘以 0.999,缩小一点点,然后再向最小点的方向移动一下。
2.4.4.2 正规方程法
正规方程结论为:
Θ = ( X T X ) − 1 X T Y \Theta=\left(X^{T} X\right)^{-1} X^{T} Y Θ=(XTX)−1XTY,其中前提条件是 X T X X^{T}X XTX 是非奇异(非退化)矩阵, 即 ∣ X T X ∣ ! = 0 \left|X^{T} X\right| != 0 ∣∣XTX∣∣!=0
正则化后,上式变为:
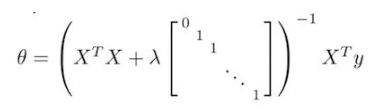
在第二周课程中,提到了正规方程中,可以通过正则化解决不可逆问题。
因此对于正规方程,正则化相当于一石二鸟。
2.4.5 逻辑回归的正则化
假设函数:
h θ ( x ) = 1 1 + e − θ T x h_{\theta}(x)=\frac{1}{1+e^{-\theta T_{x}}} hθ(x)=1+e−θTx1
代价函数:
CostFunction = F ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) logh θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] =\mathrm{F}(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \operatorname{logh}_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] =F(θ)=−m1[∑i=1my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
正则化后的损失函数:
costFunction = F ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 =\mathrm{F}(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2} =F(θ)=−m1[∑i=1my(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
迭代运算:
θ j : = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) j ∈ { 1 , 2 , 3 , 4 , ⋯ n } \theta_{j} :=\theta_{j}\left(1-\alpha \frac{\lambda}{m}\right)-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} \quad j \in\{1,2,3,4, \cdots n\} θj:=θj(1−αmλ)−αm1∑i=1m(hθ(x(i))−y(i))xj(i)j∈{1,2,3,4,⋯n}
注意:
(1) 虽然正则化在逻辑回归中的梯度下降和线性回归中表达式一致,但是由于 h θ ( x ) h_{\theta}(x) hθ(x)不同,会有很大区别
(2) θ 0 \theta_0 θ0不参与正则化
3. 课后编程作业
我将课后编程作业的参考答案上传到了github上,包括了octave版本和python版本,大家可参考使用。
https://github.com/GH-SUSAN/Machine-Learning-MarkDown/tree/master/week3
4. 总结
本周课程我们学习使用逻辑回归模型对监督学习中另一类问题即“分类问题”进行求解。
并对模型的欠拟合和过拟合进行了讨论,并使用正则化对过拟合问题进行了矫正。
逻辑回归作为重要的统计学习方法,对未来神经网络有着深远的影响,务必重点掌握。
