Colorful Tree
Colorful Tree
The path between each two different nodes is unique, of which we define the value as the number of different colors appearing in it.
Calculate the sum of values of all paths on the tree that has n(n−1)2 paths in total.
For each test case, the first line contains one positive integers n, indicating the number of node. (2≤n≤200000)
Next line contains n integers where the i-th integer represents ci, the color of node i. (1≤ci≤n)
Each of the next n−1 lines contains two positive integers x,y (1≤x,y≤n,x≠y), meaning an edge between node x and node y.
It is guaranteed that these edges form a tree.
PS:各种细节持续完善中…
题意:
一棵有n个结点的树,每个结点染上一种颜色,对于树上的每一条路径,统计其经过结点的不同颜色数,求出树上所有路径的颜色种数数量和。
思路:(根据标程所写,现根据标程写出标程的思路)
正向思维:
对于树上的每一条路径,如果某一条路径中含有颜色2,那么在这条路径上,颜色2为答案(颜色种数)贡献了“1”。由于路径较多,经过结点较多,所以正向思维实现起来比较繁琐。
逆向思维:
由于某一条路径中可以经过很多颜色相同的结点,所以我们反向考虑。考虑树上所有路径中,有哪些路径不含有某种颜色,求出其数量,然后用总路径数分别减去不含每种颜色的路径数,就可得答案。
逆向思维实现:(参照代码)
输入结点个数n,输入n个结点的颜色,根据颜色将结点分开,c[i]里面记录涂有颜色i的有哪些结点。i的取值从1~n,代表一棵结点为n的树,其所有结点的颜色最多有n种。由题意可得一棵树上总路径数为n*(n-1)/2,(任意两点间路径唯一),若所有的结点均为不同颜色且每一条路径上的结点包含所有的颜色,则结果为n*n*(n-1)/2。(这种情况很少出现,其结果为,n个结点时答案的上限,比如两个结点两种颜色时答案为2)。若结点的颜色种类数小于n,则每相对于n减少一种颜色,就有一个vector c为空,答案就减少n*(n-1)/2。而对于其他vector c不为空的情况,例如vector c[2],我们就要,求这棵树上不包含颜色2的所有路径,减去这些路径,(颜色2对这些路径没有贡献,对结果影响了“1”,减去路径其实相当于减去路径数*1)。再以此类推,可得结果。
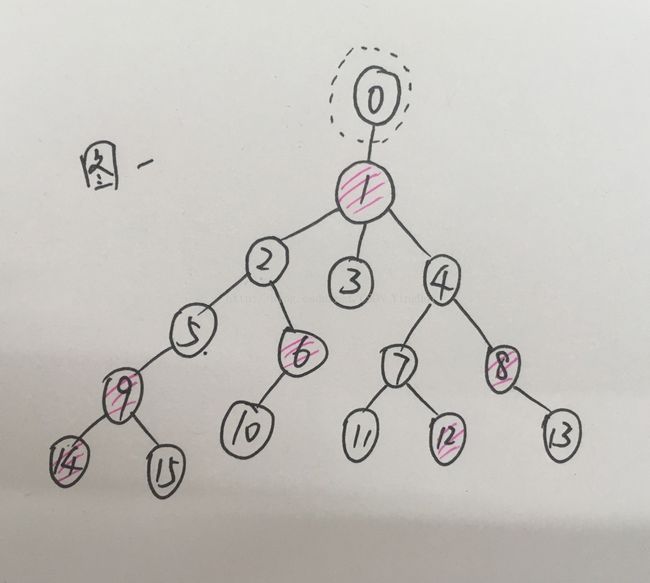
下面介绍如何计算不包含某种颜色的路径数。如颜色2。思路是删除这棵树上所有颜色为2的结点,并删除其邻边,则会把原来的树变成一个森林。求森林中每棵树的总路径数,即(结点数*(结点数-1))/2,相加则得出的这些路径均是不含有颜色2的路径。下面举例说明其代码实现过程(图一)。
对于每一种颜色,例如红色,将所有颜色为红色的结点根据dfs排序,然后对于每一个这种颜色的结点,(例如结点1),找出以这个结点为根节点的子树中,其孩子结点(2,3,4)为根节点的子树中不含该颜色的区域,(如以结点2为根节点的子树中有效区域为2-5)。其具体实现过程为,(以结点2为例)。根据lower_bound找出c[i](i为结点1的颜色)序列中dfs序不小于3(结点2的dfs序)的第一个点(即9),it=9的位置,判断it是否指向c[i]的最后一个位置或者it所代表的结点的dfs序(结点9的dfs序)是否大于子树中(以2为根节点的树)最大的dfs序(结点10的dfs序9),如果是则跳出。如果符合第一个条件说明已经是本颜色的最后一个结点,不必再循环;如果符合第二个条件则说明找到的结点并不属于这个子树,不必在这个子树中计算,则符合二者其一均应跳出。(此例不符合)。若不符合则删去size(9),k赋值为R[*it]+1=R[9]+1=7,即dfs序为7的点,即点6。而点6恰好为结点2的另一个孩子,重复处理结点6。可得最终结果为size(2)-size(9)-size(6)=7-3-2=2。其中理解时需要注意处理结点5时,没有再减去size(14),否则会造成重复。
几个小点:
1.题目中增加了一个虚拟的根节点是为了查找最上面的一部分中不含该颜色的区域。(相当于把虚根涂成该颜色后查找最上面一部分不含该颜色的区域)。
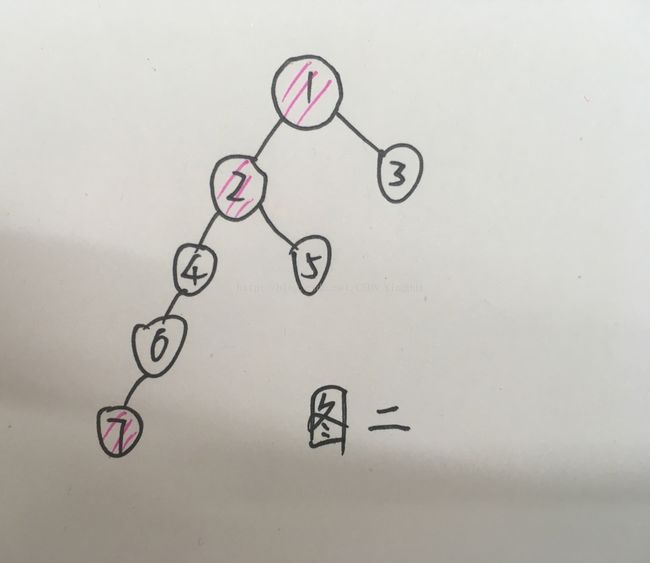
2.遍历c[i]中的每个结点(不只遍历dfs最小的点)是为了消除图二的情况。
3.程序中各数组所代表的含义:
c[i]:涂有颜色i有哪些点
e[i]:与结点i相连的结点(边数组)
L[i]:结点i的dfs序
R[i]:以i为根结点的子树中dfs序最大的点的dfs序
S[i]:以i为根节点的树共有多少个结点
f[i]:结点i的父亲结点
4.标程中涉及一些C++ 11中出现的新标准,其具体用法及适用范围还不是很清楚,对于此题,理解各数组含义及解题思路后可以对这些用法不求甚解,以后仔细学习之后再填坑。
<1>. move函数,此题中涉及ncnt的传参用法
<2>. for (auto &y : e[x]) 代表遍历e[x]中所有的元素,每次遍历时都把元素成为y
<3>. 关于it,vector用lower_bound查找到it=end指针的时候,不要输出*it。
<4>. 关于auto,auto &可以修改相应内存单元的值。
附图两张:
下面贴上标程:
#include
using namespace std;
typedef long long LL;
const int N = 200005;
int n , ca;
vector e[N] , c[N];
int L[N] , R[N] , s[N] , f[N];
void dfs(int x , int fa , int &&ncnt)
{
L[x] = ++ ncnt;
s[x] = 1 , f[x] = fa;
for (auto &y : e[x])
{
if (y != fa)
{
dfs(y , x , move(ncnt));
s[x] += s[y];
}
}
R[x] = ncnt;
}
bool cmp(const int& x , const int& y)
{
return L[x] < L[y];
}
void work()
{
for (int i = 0 ; i <= n ; ++ i)
{
c[i].clear();
e[i].clear();
}
for (int i = 1 ; i <= n ; ++ i)
{
int x;
scanf("%d" , &x);
c[x].push_back(i);
}
for (int i = 1 ; i < n ; ++ i)
{
int x , y;
scanf("%d%d" , &x , &y);
e[x].push_back(y);
e[y].push_back(x);
}
e[0].push_back(1);
dfs(0 , 0 , 0);
LL res = (LL)n * n * (n - 1) / 2; //假设n个结点颜色均不同,每种颜色都贡献了所有的路径
for (int i = 1 ; i <= n ; ++ i)
{
if (c[i].empty()) //如果为空,减一次(没有这种颜色,减掉这种颜色所贡献的路径(全部))
{
res -= (LL)n * (n - 1) / 2;
continue;
}
c[i].push_back(0);
sort(c[i].begin() , c[i].end() , cmp);
for (auto &x : c[i])
{
for (auto &y : e[x])
{
if (y == f[x]) //若为父亲结点则continue(只考虑孩子结点)
continue;
int size = s[y];
int k = L[y];
while (1)
{
L[n + 1] = k;
auto it = lower_bound(c[i].begin() , c[i].end() , n + 1 , cmp); //找以孩子结点为根节点的子树中,相同颜色的结点
if (it == c[i].end() || L[*it] > R[y])
{
break;
}
size -= s[*it];
k = R[*it] + 1; //另一棵子树
}
res -= (LL)size * (size - 1) / 2;
}
}
}
printf("Case #%d: %lld\n" , ++ ca , res);
}
int main()
{
while (~scanf("%d" , &n))
{
work();
}
return 0;
}