图论的割顶、桥和强连通分量

作为一个图论无能的蒟蒻，总算决定写一写图论的总结了

一、最小生成树（MST）另类算法和最小环问题

二、图的连通性问题基本概念

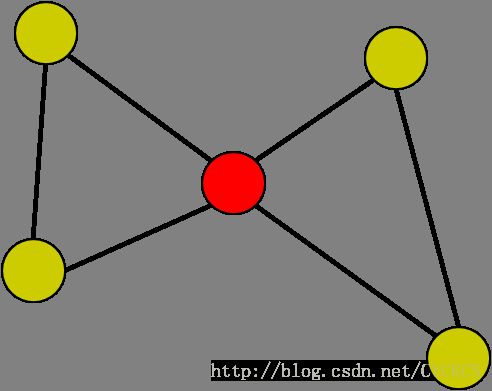
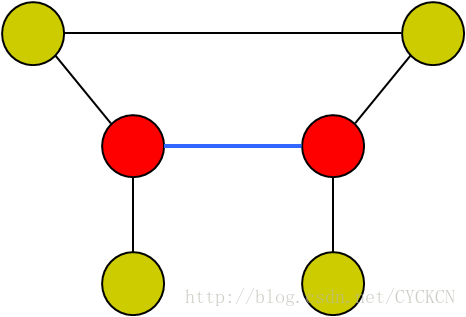
割点：删掉它之后(删掉所有跟它相连的边)，图必然会分裂成两个或两个以上的子图。
割边(桥)：删掉一条边后，图必然会分裂成两个或两个以上的子图，又称桥。
连通块
强连通子图(强连通分量(支,块))

三、联通块及其相关知识

1、DFS算法

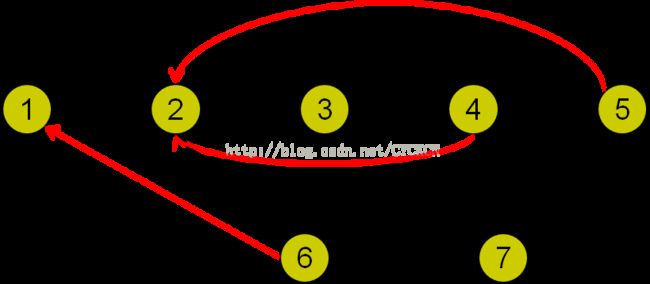
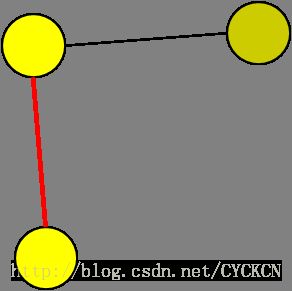
父子边用黑色标记，返祖边用红色标记；如下图，除掉返祖边之后，我们可以把它看作一棵DFS树

	dfn[v] = ++sign; //给v按照访问顺序的先后标号为sign
	for 寻找一个v的相邻节点u
		if 边uv没有被标记过
                           标记边uv;
			给边定向v→u;
                           如果u被标记过, uv为返祖边,否则记uv为父子边
			if u未被标记  DFS(u);

2、割点(一般对于无向图而言)

G是连通图，v∈V(G)，G – v 不再连通，则称v是G的割顶。

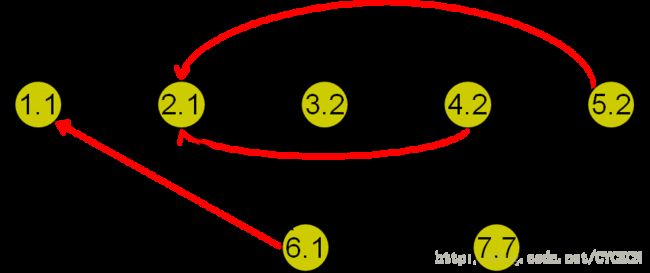
下图所示，每个点左边是dfn值，右边是low值。(经过返祖边后则停止)

	dfn[v] = ++sign; //给v按照访问顺序的先后标号为sign
	low[v] = sign; //给lowlink[v]赋初始值
	for 寻找一个v的相邻节点u
		if 边uv没有被标记过 
			标记边uv;
			给边定向v→u;
			if u未被标记过
				DFS(u); //uv是父子边，递归访问
				low[v] = min(low[v],low[u]);
				if low[u] >= dfn[v]  v是割点 
			else	low[v] = min(low[v],dfn[u]); //uv是返祖边		

3、割边(一般对于无向图而言)

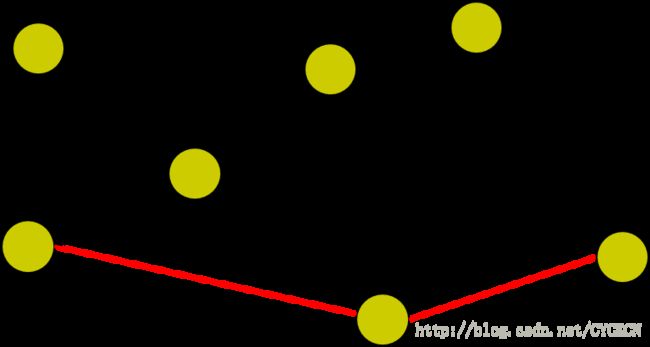
G是连通图，e∈E(G)，G – e 不再连通，则称e是G的割边，亦称做桥。

与割点类似的，我们定义low和dfn。父子边e=u→v ，当且仅当low[v] > dfn[u]的时候，e是割边。

	dfn[v] = ++sign; //给v按照访问顺序的先后标号为sign
	low[v] = sign; //给low[v]赋初始值
	for 寻找一个v的相邻节点u
		if 边uv没有被标记过
			标记边uv;
			给边定向v→u;
			if u未被标记过
				DFS(u); //uv是父子边，递归访问
				low[v] = min(low[v],low[u]);
				if low[u] > dfn[v] vu是割边
			else	low[v] = min(low[v],dfn[u]); //uv是返祖边

两个割点之间的边是否是割边?割边的两个端点是否是割点？都错

         

4、块(一般对于无向图而言)

没有割点的图叫2-连通图，亦称做块，G中成块的极大子图叫做G的块。把每个块收缩成一个点，就得到一棵树，它的边就是桥。

在求割点的算法中，当结点u的所有邻边都被访问过之后，如果lowlink[u]=dfn[u]，我们把u下方的整块和u导出作为图中的一个块。这里需要用一个栈来表示哪些元素是u代表的块。

	dfn[v] = ++sign; //给v按照访问顺序的先后标号为sign
	lowlink[v] = sign; //给lowlink[v]赋初始值
	stack[++tot] = v; //v点进栈
	for 寻找一个v的相邻节点u
		if 边uv没有被标记过
			标记边uv;
			给边定向v→u;
			if u未被标记过
				DFS(u); //uv是父子边，递归访问
				lowlink[v] = min(lowlink[v],lowlink[u]);
			else	lowlink[v] = min(lowlink[v],dfn[u]); //uv是返祖边
	if lowlink[v] == dfn[v]
		块数目number+1;
		do
			标记stack[tot]这个点为number;
			dec(tot); // 点出栈
		while( stack[tot+1] == v);

5、有向图的DFS

有向图的DFS与无向图的DFS的区别在于搜索只能顺边的方向进行，所以有向图的DFS不止一个根，因为从某个结点开始不一定就能走完所有的点。另外，有向图的DFS除了产生父子边和返祖边以外，还会有横叉边。我们这样定义它：

   u和v在已形成的DFS森林中没有直系上下关系，并且有dfn[v]>dfn[u]，则称e=uv是横叉边。 注意，没有 dfn [v]< dfn [u] 这种横叉边。

6、强连通子图(一般对于有向图而言)

···定义

将所有有向边改为无向边，如果该无向图是连通的，那么原有向图也称之为连通图。

对于图中的任意两个点A和B，同时存在一条从A到B的路径和一条从B到A的路径，则称该图为强连通图。

对于一个连通的无向图，他是一个强连通图，这里着重介绍一下有向图的强连通子图，也称做强连通分量，强连通分支和强连通分块。

···求强连通子图的算法1

一种求有向图强连通子图的算法和求无向图块的方法几乎一样，不同的是，我们需要特殊考虑一下横叉边的处理。如果e=u→v是横叉边，那么lowlink[u] := min(lowlink[u],dfn[v])这一步就无需再做 。

···求强连通子图的算法2

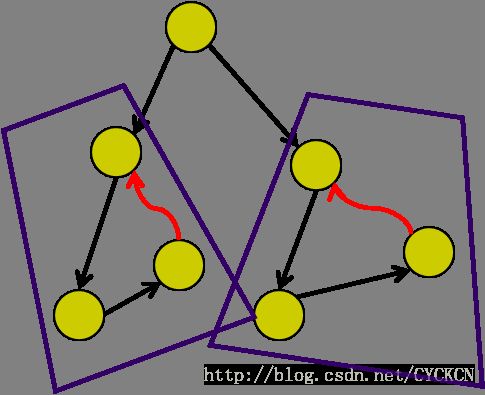
基于两次DFS的有向图强连通子图算法：

(1)对图进行DFS遍历，遍历中记下所有的dfn[v]的值。遍历的结果是构造了一座森林W1；

(2)改变图G中的每一条边的方向，构造出新的有向图Gr；

(3)按照dfn[v]由大到小的顺序对Gr进行DFS遍历。遍历的结果是构造了新的森林W2，W2中的每棵树上的顶点构成了有向图的极大强连通子图。

···有向图的压缩

将有向图中的强连通子图都压缩成为一个点之后，是否和无向图压缩之后的结果一样呢？

有向图压缩之后，连接不同结点之间的边有两种：父子边，横叉边。压缩后的图，不是一个标准意义上的树(将边看作无向)。它是一个无有向圈的有向图，即不可再压缩的图

四、练习题

1、城市备用机

#include 
#include 
#include 
#include 
#define L 300000 + 10
using namespace std;
 
struct node {
	int nxt, to;
} e[L << 1];
int n, a, b, head[L], cnt, dfn[L], son, root, vis[L], ans, num, low[L];
 
inline void add(int a, int b) {
	e[++cnt].nxt = head[a], e[cnt].to = b, head[a] = cnt;
}
 
inline void tarjan(int x) {
	dfn[x] = low[x] = ++num;
	for (int u = head[x]; u; u = e[u].nxt) {
		int v = e[u].to;
		if (!dfn[v]) {
			tarjan(v);
			if (x == root) son++;
			else {
				low[x] = min(low[v], low[x]);
				if (low[v] >= dfn[x] && !vis[x]) ans++, vis[x] = 1; 
			}
		}
		else low[x] = min(low[x], dfn[v]);
	}
}
 
int main() {
	scanf("%d", &n);
	while(scanf("%d %d", &a, &b) != EOF) add(a, b), add(b, a);
	for (int i = 1; i <= n; ++i) {
		if (!dfn[i]) {
			son = 0, root = i;
			tarjan(i);
			if (son > 1 && !vis[i]) ans++, vis[i] = 1;
		}
	}
	printf("%d\n", ans);
	for (int i = 1; i <= n; ++i) if(vis[i]) printf("%d\n", i);
	return 0;
}

2、篮球队的通讯方式

#include 
#include 
#include 
#include 
#include 
#include 
#define L 10000 + 100
using namespace std;
 
struct node{
	int nxt, to;
} e[L << 1];
vector  zhan[L];
stack  z;
int n, a, b, head[L], cnt, dfn[L], tot, low[L], q[L], top, sum, temp;
bool in[L];
 
inline void add(int a, int b) {
	e[++cnt].nxt = head[a], e[cnt].to = b, head[a] = cnt;
}
 
inline void tarjan(int x) {
	dfn[x] = low[x] = ++tot, in[x] = 1, q[++top] = x;
	for (int u = head[x]; u; u = e[u].nxt) {
		int v = e[u].to;
		if (!dfn[v]) tarjan(v), low[x] = min(low[x], low[v]);
		else if (in[v]) low[x] = min(low[x], dfn[v]);
	}
	if (low[x] == dfn[x]) {
		sum++;
		do{
			temp = q[top--]; in[temp] = 0;
			zhan[sum].push_back(temp);
		}while(temp != x);
	}
}

inline bool comp(vector a, vector b) {
	return a[0] < b[0];
}
 
int main() {
	freopen("1.in", "r", stdin);
	freopen("1.out", "w", stdout);
	scanf("%d", &n);
	while(scanf("%d %d", &a, &b) != EOF && a) add(a, b);
	for (int i = 1; i <= n; ++i) if(!dfn[i]) tarjan(i);
	for (int i = 1; i <= sum; ++i) sort(zhan[i].begin(), zhan[i].end());
	sort(zhan + 1, zhan + 1 + sum, comp);
	printf("%d\n", sum);
	for (int i = 1; i <= sum; ++i) {
		for (int j = 0; j < zhan[i].size(); ++j) printf("%d ", zhan[i][j]);
		printf("\n");
	}
	return 0;
}