Wasserstein GAN

转自：https://blog.csdn.net/shadow_guo/article/details/56003908

来自Martin Arjovsky 100 等人的“Wasserstein GAN”。

1. 简介

本文关心的问题为无监督学习问题。学习11个概率分布意味着什么？传统的回答：学习概率密度。常通过定义密度(Pθ)θ∈Rd(Pθ)θ∈Rd的参数化（parameterized）簇，并找到最大化我们数据上似然的参数来完成：若有真实数据样本{x(i)}mi=1{x(i)}i=1m，求解问题： 

maxθ∈Rd1m∑i=1mlogPθ(xi)maxθ∈Rd1m∑i=1mlogPθ(xi)

真实数据的分布PrPr给出概率密度，而PθPθ为参数化的概率密度PθPθ，那么，学习概率密度渐近等于最小化Kullback-Leibler散度KL(Pr||Pθ)KL(Pr||Pθ)。 
为使其有意义，需存在模型密度PθPθ。 但这并不是常见的处理低维流形支撑的模型流形，且意味着KL距离未被定义（或只是无穷大）。 
一般可对模型分布添加噪声项来补救。所以，经典机器学习文献中，几乎所有的生成模型都包括噪声项。最简单的情况：为覆盖所有样本，假设较高带宽的高斯噪声。众所周知，如图像生成模型，添加噪声会降低样本质量，并会模糊图像。如（最近的文章 [22]）：最大似然生成图像中每个像素时，对模型所添加噪声，噪声的最优标准差大约为0.10.1，此时已归一化像素范围至[0,1][0,1]。噪声巨大，以至于文章作者给出模型生成的样本时，未在似然上添加噪声项。换言之，图像生成问题上，添加噪声项显然不正确，但仍需用最大似然方法。

 

不再估计可能不存在的PrPr密度，可定义有固定分布p(z)p(z)的随机变量ZZ，传入11个参函数（parametric function）gθ:Z→Xgθ:Z→X（典型为一神经网络），参函数按确定的分布PθPθ来直接生成样本。改变θθ，使模型分布PθPθ接近真实数据分布PrPr。有两点好处：

• 该方法可表示受低维流形限制的分布；
• 易生成样本比了解密度的数值更有用（如图像超分辨率和语义分割中，给定输入图像，考虑输出图像的条件分布）。

总之，给定任意高维的密度，计算上难以生成样本 [15] 。

变分自编码器（VAEs） [9] 和 生成的对抗网络（GANs）[4] 为参函数生成图像方法的范例。VAEs近似样本的似然，所以，受限标准模型，需耐心调整额外的噪声项；GANs定义目标函数（包括Jensen-Shannon [4]，所有ff散度 [16] 及奇异的（exotic）合并 [6]）时更灵活，另一方面，众所周知，GANs的训练微妙且不稳定，原因见理论研究 [1]。

本文转而关注用不同的方法来度量模型分布接近真实分布的程度，或者说，定义距离或散度ρ(Pθ,Pr)ρ(Pθ,Pr)。不同距离间主要区别是它们对概率分布序列收敛的影响。当且仅当存在分布P∞P∞，使ρ(Pt,P∞)ρ(Pt,P∞)趋于00时，分布(Pt)t∈N(Pt)t∈N收敛，此时完全取决于距离ρρ的定义。通俗地说，距离ρρ引入更弱的拓扑，使分布序列更易收敛。第22节澄清概率距离在收敛上的不同。

当ρρ下的收敛序列集为ρ′ρ′下的收敛序列集的超集时，ρρ引入的拓扑弱于ρ′ρ′引入的拓扑。

为优化参数θθ，当然希望定义的模型分布PθPθ可使映射θ→Pθθ→Pθ连续。连续性意味着当参数序列θtθt收敛至θθ时，分布PθtPθt也收敛至分布PθPθ。然而，分布序列PθtPθt收敛取决于如何计算分布间的距离。距离越弱，分布序列越易收敛，因此越易定义从θθ空间到PθPθ空间的连续映射。考虑映射θ→Pθθ→Pθ连续是因为：若ρρ为两分布间的距离，希望损失函数θ→ρ(Pθ,Pr)θ→ρ(Pθ,Pr)连续，等价于使用分布ρρ间的距离时，映射θ→Pθθ→Pθ连续。

本文的贡献有：

• 第22节，全面地理论分析学习分布时，相比流行的概率距离和散度，推土机距离（Earth Mover distance）的表现。
• 第33节，定义一种GAN，称其为Wasserstein-GAN。有效合理地近似EM距离，最小化EM距离。并理论上显示对应的优化问题可靠。
• 第44节，经验上显示WGANs解决了GANs主要的训练问题。特别地，（i）训练WGANs不要求小心平衡生成器和判别器的训练；（ii）不要求小心设计网络结构；（iii）显著减少GANs中典型的模式减少（mode dropping）现象；（iv）训练判别器至最优来连续估计EM距离；（v）绘制学习曲线有助调试和超参数搜索，并与观测到的图像质量紧密关联。

2. 不同的距离

标记介绍。令XX为紧度量集（如图像空间[0,1]d[0,1]d）101，并令ΣΣ为XX所有Borel子集的集合。令Prob(X)Prob(X)为定义在XX上的概率度量空间。

样本方差不为00，所以为Borel子集 102 。

定义22个分布Pr,Pg∈Prob(X)Pr,Pg∈Prob(X)间基本的距离和散度：

• 全变差（Total Variation，TV）距离 

  σ(Pr,Pg)=supA∈Σ|Pr(A)−Pg(A)|.σ(Pr,Pg)=supA∈Σ|Pr(A)−Pg(A)|.

• Kullback-Leibler（KL）距离 103 

  KL(Pr||Pg)=∫log(Pr(x)Pg(x))Pr(x)dμ(x),KL(Pr||Pg)=∫log(Pr(x)Pg(x))Pr(x)dμ(x),

其中，假设PrPr和PgPg绝对连续，关于定义在XX上用相同的度量μμ输出密度。KL散度不对称，且当存在点使Pg(x)=0且Pr(x)>0Pg(x)=0且Pr(x)>0时，KL散度可能为无穷大。

概率分布Pr∈Prob(X)Pr∈Prob(X)输出关于μμ的概率密度pr(x)pr(x)，即，∀A∈Σ,Pr(A)=∫APr(x)dμ(x)∀A∈Σ,Pr(A)=∫APr(x)dμ(x)，当且仅当Pr(x)Pr(x)关于μμ绝对连续，即，∀A∈Σ,μ(A)=0→Pr(A)=0∀A∈Σ,μ(A)=0→Pr(A)=0。

• Jensen-Shannon（JS）距离 

  JS(Pr,Pg)=12KL(Pr||Pm)+12KL(Pg||Pm),JS(Pr,Pg)=12KL(Pr||Pm)+12KL(Pg||Pm),

  
  其中，Pm=Pr+Pg2Pm=Pr+Pg2。JS散度对称，且可选μ=Pmμ=Pm，此时JS散度总有定义（defined）。

   

• 推土机（Earth-Mover，EM）距离 

  W(Pr,Pg)=infγ∈∏(Pr,Pg)E(x,y)∼γ[||x−y||],(1)W(Pr,Pg)=infγ∈∏(Pr,Pg)E(x,y)∼γ[||x−y||],(1)

  
  其中，∏(Pr,Pg)∏(Pr,Pg)为所有联合分布γ(x,y)γ(x,y)的集合，它的边缘分布分别为PrPr和PgPg。直观上看，γ(x,y)γ(x,y)表明：为转移分布PrPr至分布PgPg，必须从xx到yy来转移多少“质量”。那么，EM距离为最优传输计划（optimal transport plan）的“代价”。

   

EM距离求下确界，即至少要转移多少“质量”。所以，原文中，作者用“must”描述。

后面举例说明用EM距离来收敛概率分布序列多简单，但上面定义的其它距离和散度无法收敛。

例1 （学习平行线）。令Z∼U[0,1]Z∼U[0,1]（单位区间上的均匀分布）。令P0P0为(0,Z)∈R2(0,Z)∈R2的分布（xx轴上为00，yy轴上为随机变量ZZ，经过原点的垂直线段上的均匀分布）。令gθ(z)=(θ,z),θgθ(z)=(θ,z),θ为单个实参数。此时有：

• W(P0,Pθ)=|θ|,W(P0,Pθ)=|θ|,
• JS(P0,Pθ)={log2,if θ≠0,0,if θ=0,JS(P0,Pθ)={log2,if θ≠0,0,if θ=0,
• KL(Pθ||P0)=KL(P0||Pθ)={+∞,if θ≠0,0,if θ=0,KL(Pθ||P0)=KL(P0||Pθ)={+∞,if θ≠0,0,if θ=0,
• σ(P0||Pθ)={1,if θ≠0,0,if θ=0.σ(P0||Pθ)={1,if θ≠0,0,if θ=0.

• 已知：P0={1,if x=0,0≤y≤1,0,otherwise.P0={1,if x=0,0≤y≤1,0,otherwise., Pθ={1,if x=θ,0≤y≤1,0,otherwise.Pθ={1,if x=θ,0≤y≤1,0,otherwise. 
  θ≠0θ≠0时， 
  KL(P0||Pθ)=∑x,y∈R2P0(x,y)logP0(x,y)−∑x,y∈R2P0(x,y)logPθ(x,y)=0log0+1log1−(1log0+0log1)=0+0−(−∞)+0=+∞=KL(Pθ||P0)KL(P0||Pθ)=∑x,y∈R2P0(x,y)logP0(x,y)−∑x,y∈R2P0(x,y)logPθ(x,y)=0log0+1log1−(1log0+0log1)=0+0−(−∞)+0=+∞=KL(Pθ||P0) 
  θ=0θ=0时， 
  KL(P0||Pθ)=KL(P0||P0)=0log0+1log1=0KL(P0||Pθ)=KL(P0||P0)=0log0+1log1=0

• 已知：Pm=Pr+Pg2=⎧⎩⎨0.5,if x=0,0≤y≤1,0.5,if x=θ,0≤y≤1,0,otherwise.Pm=Pr+Pg2={0.5,if x=0,0≤y≤1,0.5,if x=θ,0≤y≤1,0,otherwise.，JS(P0||Pθ)=12KL(P0||Pm)+12KL(Pθ||Pm)JS(P0||Pθ)=12KL(P0||Pm)+12KL(Pθ||Pm) 
  θ≠0θ≠0时， 
  KL(P0||Pm)=0log0+1log1−(1log0.5+0log0.5+0log0)=log2=KL(Pθ||Pm)→JS(P0||Pθ)=log2KL(P0||Pm)=0log0+1log1−(1log0.5+0log0.5+0log0)=log2=KL(Pθ||Pm)→JS(P0||Pθ)=log2 
  θ=0θ=0时， 
  KL(P0||Pm)=KL(P0||P0)=0→JS(P0||Pθ)=0KL(P0||Pm)=KL(P0||P0)=0→JS(P0||Pθ)=0

• 本例的两条线段相距θ，||x−y||≡θ→θ，||x−y||≡θ→ 两条线段间距离的期望的下确界为θθ。
• P0P0和PθPθ表示概率分布，范围为[0,1]→|P0−Pθ|[0,1]→|P0−Pθ|的上确界为11（θ≠0θ≠0时）或00（θ=0θ=0时）。

当θ→0θ→0时，EM距离使序列(Pθt)t∈N(Pθt)t∈N收敛至P0P0，但用JS，KL，逆KL或TV散度时不会收敛。图11为EM距离和JS距离。

例11说明EM距离上梯度下降可学到低维流形上的概率分布。不可用其它距离，因它们的损失函数甚至不连续。即使该例基于不相交支集的分布，当支集非空但包含00测度集时，结论同样成立。当22个低维以任意位置相交时 [1]，碰巧也成立。 
因Wasserstein距离比JS距离更弱，问题变成：温和假设下，W(Pr,Pθ)W(Pr,Pθ)是否为关于θθ的连续损失函数。

定理 1. 令PrPr为XX上的固定分布。令ZZ为另11个空间ZZ上的随机变量（如：高斯分布空间）。令g:Z×Rd→Xg:Z×Rd→X为11个函数。用zz作第11个坐标，θθ作第22个坐标来表示gθ(z)gθ(z)。令PθPθ为gθ(z)gθ(z)的分布。那么， 
1. 若gg在θθ上连续，W(Pr,Pθ)W(Pr,Pθ)在θθ上也连续。 
2. 若gg为局部Lipschitz，并满足规则假设11，则W(Pr,Pθ)W(Pr,Pθ)处处连续，几乎处处可微。 
3. 对JS散度和所有KL散度，声明1−21−2为假。

证明见附录CC。

后面推论告诉我们：用神经网络来最小化EM距离（至少理论上）可行。

推论 1. 令gθgθ为任意用θθ参数化的前向神经网络，且p(z)p(z)为zz上的先验，使得Ez∼p(z)[||z||]<∞Ez∼p(z)[||z||]<∞（如，高斯分布，均匀分布等）。则满足假设11，因此，W(Pr,Pθ)W(Pr,Pθ)处处连续，几乎处处可微。

证明见附录CC。

所有这些说明：对我们的问题，至少与JS散度相比，EM距离作损失函数更合理。后面定理描述这些距离和散度引入拓扑的相对强度：KL最强，紧随JS和TV，EM最弱。

推论 2. 令PP为紧空间XX上的分布，且(Pn)n∈N(Pn)n∈N为XX上的分布序列。那么，当n→0n→0时，考虑所有的限制， 
1. 下面声明等价 
- σ(Pn,P)→0σ(Pn,P)→0，σσ为全变差距离； 
- JS(Pn,P)→0JS(Pn,P)→0，JSJS为Jensen-Shannon散度。 
2. 下面声明等价 
- W(Pn,P)→0W(Pn,P)→0； 
- Pn⟶DPPn⟶DP，其中，⟶D⟶D表示关于随机变量的分布的收敛。 
3. KL(Pn||P)→0KL(Pn||P)→0或KL(P||Pn)→0KL(P||Pn)→0隐含（imply）声明(1)(1)。 
4. 声明(1)(1)隐含声明(2)(2)。

证明见附录CC。

这里强调的事实：学习低维流形支撑的分布时，KL，JS和TV距离为不合理的损失函数。但此时EM距离却合理：

• EM距离可使概率序列收敛至真实数据的概率分布，其它距离不可收敛；
• EM距离的损失函数连续，可用梯度下降学习低维流形上的概率分布；其它距离的损失函数不连续；
• EM距离引入的拓扑相对强度最弱。

3. Wasserstein GAN

定理22指出，W(Pr,Pθ)W(Pr,Pθ)可能比JS(Pr,Pθ)JS(Pr,Pθ)有更好的属性。(1)(1)中的下确界很难解。 
另一方面，由Kantorovich-Rubinstein二重性（duality） [21] 知 

W(Pr,Pθ)=sup||f||L≤1Ex∼Pr[f(x)]−Ex∼Pθ[f(x)](2)W(Pr,Pθ)=sup||f||L≤1Ex∼Pr[f(x)]−Ex∼Pθ[f(x)](2)

其中，上确界覆盖所有11-Lipschitz函数f:X→Rf:X→R。注意到，若替换||f||L≤1||f||L≤1为||f||L≤K||f||L≤K（考虑常数KKde KK-Lipschitz），则EM距离变为K⋅W(Pr,Pθ)K⋅W(Pr,Pθ)。因此，若有参函数簇{fw}w∈W{fw}w∈W，对某些KK，参函数都为KK-Lipschitz，考虑求解： 

maxw∈WEx∼Pr[fw(x)]−Ez∼p(z)[fw(gθ(z))](3)maxw∈WEx∼Pr[fw(x)]−Ez∼p(z)[fw(gθ(z))](3)

且对某些w∈Ww∈W（类似证明估计器一致性时的假设的一强假设），当获得(2)(2)中的上确界时，求解过程计算出的W(Pr,Pθ)W(Pr,Pθ)能达到乘常数KK。进一步，考虑估计Ez∼p(z)[∇θfw(gθ(z))]Ez∼p(z)[∇θfw(gθ(z))]反传方程(2)(2)来求导W(Pr,Pθ)W(Pr,Pθ)。虽这全是直觉，现在证明最优假设下该过程是有原则的（principled）。

 

定理 3. 令PrPr为任意分布。令PθPθ为gθ(Z)gθ(Z)的分布（ZZ为随机变量，该分布的概率密度为pp，gθgθ为满足假设11的函数）。那么，对问题 

max||f||L≤1Ex∼Pr[f(x)]−Ex∼Pθ[f(x)]max||f||L≤1Ex∼Pr[f(x)]−Ex∼Pθ[f(x)]

存在解f:X→Rf:X→R，当PrPr和PθPθ都为良定时，有： 

∇θW(Pr,Pθ)=−Ez∼p(z)[∇θf(gθ(z))]∇θW(Pr,Pθ)=−Ez∼p(z)[∇θf(gθ(z))]

 

证明见附录CC。

接着，最大化方程(2)(2)来找函数ff。为近似求解ff，用紧空间XX中的权重ww来参数化一神经网络，训练该网络。然后，同典型的GAN，用Ez∼p(z)[∇θfw(gθ(z))]Ez∼p(z)[∇θfw(gθ(z))]反传。注意到WW紧致，则对某些仅取决WW（而非个别网络权重）的KK，所有函数fwfw将为KK-Lipschitz。因此，近似(2)(2)至一无关的缩放因子和“评价者”（critic）fwfw的容量。为使参数ww落入紧空间，每次梯度更新后夹紧权重至固定的范围即可（假设W=[−0.01,0.01]lW=[−0.01,0.01]l）。方法11描述Wasserstein生成对抗网络（WGAN）过程。

注：“评价者”和“判别器”应是一回事，我更习惯用GAN框架来说明，所以后面统一用“判别器”替换“评价者”。原作者用两个不同的词，考虑到后面比较GAN判别器（判别器）和WGAN判别器（评价者）时便于说明。所以，这里，WGAN与GAN比较时，将“评价者”替换为“WGAN判别器”；无比较时，仍用“判别器”。 
θθ为生成网络的参数，决定生成模型的分布与真实数据分布的距离；ww为判别网络的参数，最大化EM距离损失函数来获得最优判别网络的参数。

EM距离处处连续，且几乎处处可微，所以应该能训练判别器至最优。参数简单，训练判别器的时间越长，得到的EM距离的梯度越可靠。

判别器越好，JS散度的梯度越可靠。但会因JS散度局部饱和，真实梯度为00，梯度消失，见图11和 [1] 中定理2.42.4。

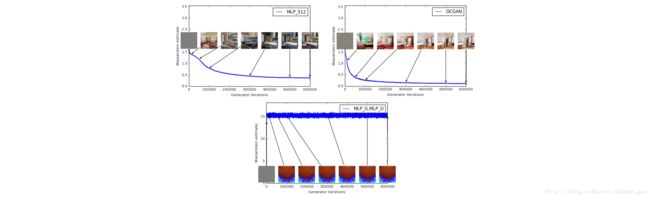
图22中，为证明这点，训练GAN判别器和WGAN判别器至最优。GAN判别器很快学会区分真伪数据，同期望一样，并未提供可靠的梯度信息。然而，WGAN判别器不饱和，收敛至线性函数并处处给出很明确的梯度；约束梯度限制了函数，使其可能在空间不同部分至多线性增长。

训练WGAN判别器至最优不会破坏（collapse）模式。固定判别器来找最优生成器是指使判别器输出最大值的点上变量增量的和 [11]。

后面介绍新方法的实际效益，深入比较WGAN与传统GAN。

4. 经验结果

用Wasserstein-GAN方法生成图像，相比标准GANs，有显著的实际效益，主要有两点：

• 有意义的损失度量：关联生成器的收敛性和样本质量；
• 优化过程更稳定。

4.1 实验过程

生成图像实验。真实数据分布为LSUN-卧室数据集 [23] - 室内卧室自然图像的集合。基线比较为DCGAN，DCGAN用−logD−logD，标准的GAN过程训练一卷积网络结构的GAN。生成样本为分辨率64×6464×64的33通道图像。

4.2 有意义的损失度量

因每次生成器更新前（方法11的行1010），WGAN试图训练出相对较好的WGAN判别器ff（方法11的行2−82−8），此时损失函数为估计EM距离，上界为某常数，该常数与我们约束ff的Lipschitz常数有关。

实验11表明估计EM距离与生成样本密切相关。除卷积的DCGAN结构，用44层ReLU-MLP（每层包含512512个隐含单元）只替换生成器或同时替换生成器和判别器来运行实验。

图33为33种结构的WGAN训练时，估计的EM距离的变化。该图清楚显示，曲线与生成样本的视觉质量密切相关。

然而，还不能定量评估生成模型。常数缩放因子取决于WGAN判别器的结构，所以，不同的WGAN判别器模型间难以比较。甚至，实际上判别器容量有限，所以，难以了解真实的EM距离与估计的EM距离多接近。可话说回来，用该损失度量重复且成功验证了实验，相比之前GAN的训练能力有巨大的提高。

相反，图44为GAN训练时，估计的JS散度的变化。更确切地，GAN训练时，训练判别器来最大化： 

L(D,gθ)=Ex∼Pr[logD(x)]+Ex∼Pθ[log(1−D(x))]L(D,gθ)=Ex∼Pr[logD(x)]+Ex∼Pθ[log(1−D(x))]

 

注：x∼Prx∼Pr时，xx为真实样本，希望D(x)↑D(x)↑；x∼Pθx∼Pθ时，xx为生成样本，希望D(x)↓D(x)↓。

其中，L(D,gθ)L(D,gθ)的下界为2JS(Pr,Pθ)−2log22JS(Pr,Pθ)−2log2。图中，值12L(D,gθ)+log212L(D,gθ)+log2为JS距离的下界。

JS距离的下界与样本质量关系很差。估计的JS距离通常保持不变或上升（而非下降）。实际上，JS估计值常保持为接近log2≈0.69log2≈0.69（JS距离的最大值）。换句话说，JS距离饱和，GAN判别器损失为00，某些情况下（DCGAN生成器，右上图）生成样本有意义，其它情况下被破坏为无意义图像。该现象的理论解释见 [1]，强调见 [11]。

用−logD−logD时，判别器损失与生成器损失不同。附录的图88绘制相同的图，但用生成器损失（而非判别器损失）。结论不变。

负面结果：当对WGAN判别器用基于动量的优化方法（如Adam）或用很高的学习率时，训练WGAN会偶尔不稳定。因WGAN判别器的损失并非稳态，基于动量的方法可能会表现更糟。因损失爆炸和生成样本变差时，Adam步与梯度的余弦角变为负值，所以动量可能为潜在的原因。训练不稳定时，余弦角必为负值。很不平稳时，改用RMSProp效果不错。

4.3 改善稳定性

可训练WGAN判别器至最优。训练判别器时，仅需为生成器提供训练其它网络时所用到的损失。不再需合理均衡生成器和判别器的容量。判别器越好，训练生成器所用梯度的质量越高。

改变生成器的结构时，WGAN比其它GANs更鲁棒。为此，33个不同的生成器结构上运行实验：（1）卷积DCGAN生成器；（2）卷积DCGAN生成器，不带块归一化，滤波器数目不变；（3）512512个隐含单元组成的44层ReLU-MLP。后面22中用GANs表现很差。所以，为WGAN判别器和GAN判别器保留卷积DCGAN结构。 
图55，图66和图77显示用到WGAN和GAN时，33种结构生成的样本。整页的生成样本见附录FF。样本未经优选。

实验中，从未见过用WGAN时模式被破坏。

5. 相关工作

积分概率度量（Integral Probability Metric，IPMs）上有很多工作。给定从XX到RR的函数集合，定义 

dF(Pr,Pθ)=supf∈FEx∼Pr[f(x)]−Ex∼Pθ[f(x)](4)dF(Pr,Pθ)=supf∈FEx∼Pr[f(x)]−Ex∼Pθ[f(x)](4)

为关联函数类FF的积分概率度量。易证对任意f∈Ff∈F，有−f∈F−f∈F，则dFdF为非负，满足三角不等式，且对称。因此，dFdF为Prob(X)Prob(X)的伪距离。 
IPMs可能公式相似，但不同的函数类会得到完全不同度量。

 

• 由Kantorovich-Rubinstein对偶可知，当FF为1−Lipschitz1−Lipschitz函数集合时，W(Pr,Pθ)=dF(Pr,Pθ)W(Pr,Pθ)=dF(Pr,Pθ)。进一步，若FF为K−LipschitzK−Lipschitz函数，则K⋅W(Pr,Pθ)=dF(Pr,Pθ)K⋅W(Pr,Pθ)=dF(Pr,Pθ)。
• 当FF为所有−1−1到11之间的可测量函数（或所有[−1,1][−1,1]上的连续函数）时，恢复为全变差距离：dF(Pr,Pθ)=σ(Pr,Pθ)dF(Pr,Pθ)=σ(Pr,Pθ) [14]。这告诉我们损失函数从1−Lipschitz1−Lipschitz函数变至1−1−有界函数，大大改变了空间的拓扑和dF(Pr,Pθ)dF(Pr,Pθ)的正则性（regularity）（见定理11和定理22）。 
  -可认为基于能量的GANs（EBGANs）是用全变差距离的生成方法。附录DD中声明和进一步证明这一关联,关键为判别器作为函数ff来最大化方程44，唯一的限制是对常数mm，函数输出约束在[0,m][0,m]。取决于无关优化的常数缩放因子，同样可约束至[−1,1][−1,1]。因此，当判别器接近最优时，生成器的代价将逼近全变差距离σ(Pr,Pθ)σ(Pr,Pθ)。 
  因全变差距离与JS散度的正则性相似，可看出，无论是否能训练判别器至最优，EBGANs与经典的GANs问题相同，因此它的梯度也很不完美。
• 当F={f∈H:||f||inf≤1}F={f∈H:||f||inf≤1}（其中，HH为关联给定核kk的再生核Hilbert空间（Reproducing Kernel Hilbert Space，RKHS），核kk：X×X→RX×X→R）时，最大均值矛盾（Maximum Mean Discrepancy，MMD）[5] 为积分概率度量的特殊情况。如 [5] 中所证，MMD只是个合适的度量，且当核通用时不仅是伪度量。具体地，当H=L2(X,m)H=L2(X,m)时，XX上用归一化Lebesgue度量FF，可知FF中包含{f∈Cb(x),||f||∞≤1}{f∈Cb(x),||f||∞≤1}，因此dF(Pr,Pθ)≤σ(Pr,Pθ)dF(Pr,Pθ)≤σ(Pr,Pθ)。所以，以MMD距离为损失函数的正则性与全变差距离的正则性同样差。然而这是非常极端的例子，因为需要很强大的核来近似L2L2。但即使高斯核也仅能检测微小的噪声模式 [19]。尤其当使用低带宽的核时，距离可能接近类似全变差距离或JS距离的饱和方法。显然不需要每个核都如此，弄清不同MMDs如何及哪些更接近Wasserstein距离或全变差距离也很有趣。 
  MMD的优势为用核方法后无需为RKHS球空间来训练单独的网络来最大化方程(4)(4)。然而，MMD的劣势为计算代价随用于估计(4)(4)中期望的样本数目二次增长；MMD可伸缩性有限，因此无法用于许多现实应用。线性计算代价估计ＭＭＤ距离大多时候会很有用，但样本复杂度太高。
• 生成矩匹配网络（Generative Moment Match Nework，GMMD）类似MMD。反传方程(4)(4)的核化形式，直接优化dMMD(Pr,Pθ)dMMD(Pr,Pθ)（当FF为前面项时的IPM，见P12）。如前所述，不要求单独的网络来近似最大化方程(4)(4)。然而，GMMNs应用有限，部分原因是样本数目的函数为二次代价，用低带宽核时梯度会消失。并且实际用到的一些核不适合如自然图像等高维样本空间中获得的距离非常差。[18]　中表明，为让典型的高斯MMD测试可靠，需样本数目与维度数目线性增长。估计方程(4)(4)中时用的块，MMD的计算代价与样本数目二次增长。有可靠的估计器的代价与维度数目二次增长，不适用高维问题。如64×6464×64大小的标准图像，所需小块的大小至少40964096（不考虑　[18]　边界中的常数，使样本数目更多）,且每次迭代的总代价为4096240962。当用标准的块大小64×6464×64时，比11次GAN迭代多55个数量级。 
  话虽如此，比较MMDs的理论样本复杂度和GANs的经验样本复杂度时（一般会更高），对MMD不公平。然而，原GMMN文章中用到的小块大小为10001000，远大于标准的3232或6464（即使出现二次计算代价时）。尽管存在线性计算代价作样本数目的函数，样本复杂度仍更高。就我们所知，生成领域尚未应用GMMNs。

6. 结论

介绍WGAN，可替换传统GAN的训练。新模型中，提高了学习的稳定性，克服了模式被破坏等问题，并提供方便调试和超参数搜索的学习曲线。进一步，显示对应的优化问题合理，并为分布间其它距离的深入关联提供理论工作。

全文未经他人校正，如有问题欢迎指出。

7. 小记

并不是数学出身，但后面的证明还是看了。考虑到最近贼忙以及附录部分的编辑量，所以先忘了它吧… 但附录部分如有问题欢迎讨论。嗯，共同进步… ٩(๑òωó๑)۶