欢迎使用CSDN-markdown编辑器
1、 单纯形法算法源代码:
package com.yinhong;
import java.util.Scanner;
/**
* @author 作者 :hong
* @version 创建时间:2016年11月24日 上午10:12:30
* 整体思路:
* //单纯形表
* //计算σi,找出最大的非负的那个检验数σk
* //然后,根据σk的值,计算出θ比,找出θ比值最小的非负值所在的行。
* //确定主元素,换入变量和换出变量
* //根据变换公式进行变换
* //判断是否为最优解形式,或者已经无法计算,无最优解。否则继续进行迭代运算。
*注意点:判断求解得是最大化还是最小化
* 类说明
*/
public class algorithm {
final static int N = 100;
final static int M = 100;
public static void main(String[] args) {
// TODO Auto-generated method stub
double a[][] = new double[M][N];//存放线性方程组的技术系数的值
double b[] = new double[M];//存放约束条件中,限额系数的值
double c[] = new double[M];//存放基变量量的价值系数值
int x[] = new int[M];//存放基向量的下标值
double q[] = new double[N];//存放计算之后的σi的值
double p[] = new double[N];//存放变量的价值系数值
int visit[] = new int[N];//用来标记当前下标的决策变量是不是基变量,如果是基变量,则为1.否则标记为0
int l = -1,k = -1,v = -1;//l存放主元素的横坐标值,k存放的是纵坐标值,v标记换出变量的下标值,k标记换入变量的下标值;
Scanner in = new Scanner(System.in);
System.out.println("输入求解的是最大值,还是最小值,如果是求解最大值,输入1,求解的是最小值,输入0:");
//我们假设要求解得线性规划问题的初始基,在刚开始输入线性规划方程组的时候就已经确定了。
int flag = in.nextInt();//标记求解的是最大值问题还是最小值问题
int n,m;//输入求解的方程组的维数
System.out.println("请输入求解的方程组的维数:m*n");
m = in.nextInt();
n = in.nextInt();
System.out.println("求解的方程组的维数为"+m+"*"+n+"维");
System.out.println("请输入求解的目标函数的价值系数值:");
for(int i=0;i0;//初始化所有的变量均为非基变量
p[i]=in.nextDouble();
//System.out.print("p["+i+"]="+p[i]+"\t");
}
System.out.println();
System.out.println("请输入技术系数的值:");
//输入线性方程组
for(int i=0;ifor(int j=0;jin.nextDouble();
//System.out.println("a["+i+"]["+j+"]="+a[i][j]+"\t");
}
System.out.println();
}
//输入约束条件的限额系数的值
System.out.println("请输入限额系数的值:");
for(int i=0;iin.nextDouble();
}
System.out.println("请输入基变量的下标值:");
//输入初始可行基的下标值
for(int i=0;iin.nextInt();
c[i] = p[x[i]];//基变量的价值系数的值
//System.out.print("c["+i+"]="+c[i]+"\t");
visit[x[i]] = 1;//标记基变量
}
int ii = 0;
int tag1 = 0;//用来标记是否需要跳出循环运算
//一直迭代运算,对于求解最大化的线性规划问题,直到检验数均小于或等于0,或者没有最优解(没有换出变量)
//而对于求解最小化的线性规划问题,则是直到所有的检验数都大于或者等于0,而且每次挑选的检验数都是最小的检验数
while(true)
{
if(tag1==1)
break;
//System.out.println("第"+(ii++)+"次循环");//用来检验循环进行了几次
double tag = 0;//用来标记检验数是否均小于或者等于0
//开始计算非基变量检验数的值
for(int i=0;iif(visit[i]!=1)//非基变量
{
double sum = 0;
for(int j=0;jelse
q[i] = 0;
//如果求解的是最大化,则找出并且标记非基变量中检验数最大的下标值
if(flag == 1)
{
if(tag-q[i]<0)
{
tag = q[i];
k = i;
}
}
else //求解的是最小化问题,找出最小的检验数
{
if(tag-q[i]>0)
{
tag = q[i];
k = i;
}
}
System.out.print("q["+i+"]="+q[i]+"\t\t");
}
//System.out.println(tag==0);
System.out.println("检验数的值为:"+tag);
if(tag != 0)//存在换入变量,进行迭代运算
{
//根据最小比值规则,进行计算
double min = 9999.0;
int count = 0;//方便判断是否有可以替换的换入变量
System.out.println("换入变量下标为:"+k);
for(int i=0;iif(b[i]>0&&a[i][k]>0)
{
double w = b[i]/a[i][k];
//System.out.println("b["+i+"]"+b[i]+"w="+w);
if(w-min<0)
{
min = w;
l = i;//换出变量所占的行
v = x[i];//标记换出变量的下标
}
}
else
{
count++;
//System.out.print("count="+count+"\t");
}
}
System.out.println("换出变量下标为:"+v);
System.out.println("l="+l);
System.out.println(a[l][k]);
if(count == n)
{
System.out.println("无可以换出的变量,该线性方程组没有最优解");
tag1 = 1;
continue;
}
else
{
//找到了主元素a[l][k],开始使用变换公式进行变换
//暂时存放上一次的状态。这个出过错误,因为我们进行变换之后,引用的值可能不会是上一次的值,所以需要另外用数组存放起来。
double a1[][] = new double[M][N];//存放线性方程组的技术系数的值
double b1[] = new double[M];//存放约束条件中,限额系数的值
double c1[] = new double[M];//存放基变量量的价值系数值
int x1[] = new int[M];//存放基向量的下标值
double q1[] = new double[N];//存放计算之后的σi的值
double p1[] = new double[N];//存放变量的价值系数值
for(int i=0;ifor(int j=0;jout.println("变换之后的值为:");
for(int i=0;ifor(int j=0;j//对技术系数进行变换
if(j==k&&i!=l)
{
a[i][j] = 0;
System.out.print("a["+i+"]["+j+"]="+a[i][j]+"\t");
continue;
}
if(i==l)
{
a[i][j]=a1[i][j]/a1[l][k];
}
else
{
a[i][j] = a1[i][j] - ((a1[i][k]*a1[l][j])/a1[l][k]);
//System.out.print("a["+i+"]["+k+"]="+a1[i][k]);
//System.out.print("a["+l+"]["+j+"]="+a1[l][j]);
}
System.out.print("a["+i+"]["+j+"]="+a[i][j]+"\t");
}
//对限额系数进行变换
if(i==l)
{
b[l] = b1[l]/a1[l][k];
}
else
{
b[i] = b1[i] - ((b1[l]*a1[i][k])/a1[l][k]);
//System.out.println(b1[i]+" "+a1[i][k]+" "+b1[l]+" "+a1[l][k]);
}
System.out.println("b["+i+"]="+b[i]);
//判断是否已经遍历到了换出变量,如果已经遍历到了换出变量,那么就要对换出变量进行变换
if(v==x[i])
{
visit[x[i]] = 0;//标记为非基变量
x[i] = k;
c[i] = p[k];
visit[x[i]] = 1;//标记为基变量
//System.out.println("x["+i+"]="+x[i]);
//System.out.println("c["+i+"]="+c[i]);
}
}
}
}
else
{
//否则结束计算
double sum = 0;
for(int i=0;ifor(int j=0;jif(x[j]==i)
{
System.out.print(p[i]+"\t");
p[i] = p[i]*b[j];
System.out.println("b["+j+"]="+b[j]+"\t");
sum+=p[i];
break;
}
}
}
System.out.println();
System.out.println("结束迭代运算,最终的目标函数值为: "+sum);
tag1 = 1;
continue;//跳出循环
}
}
}
}
测试样例:
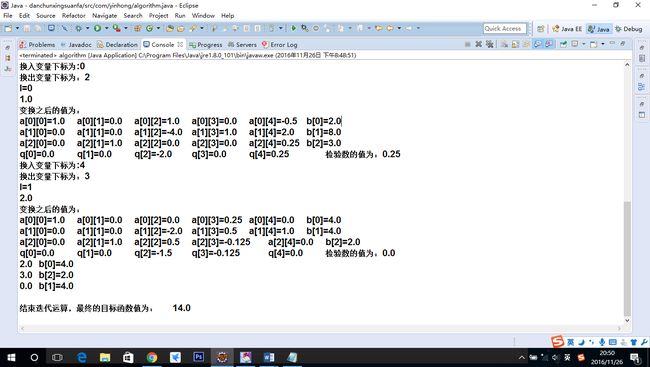
样例一:(测试求最大值)
输入求解的是最大值,还是最小值,如果是求解最大值,输入1,求解的是最小值,输入0:
1
请输入求解的方程组的维数:m*n
3
5
求解的方程组的维数为3*5维
请输入求解的目标函数的价值系数值:
2 3 0 0 0
请输入技术系数的值
1 2 1 0 0 4 0 0 1 0 0 4 0 0 1
请输入限额系数的值
8 16 12
请输入基变量的下标值
2 3 4
结果截屏:
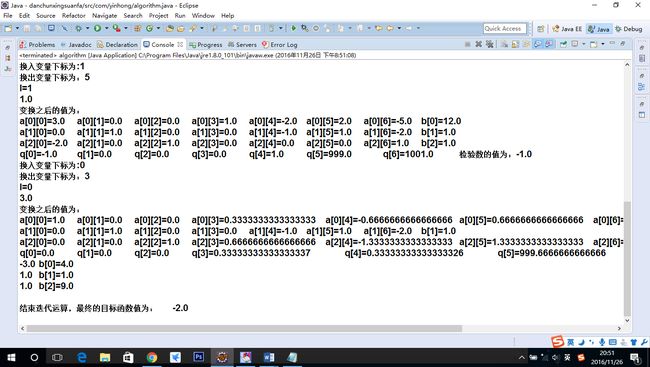
样例二:(测试求最小值)
输入求解的是最大值,还是最小值,如果是求解最大值,输入1,求解的是最小值,输入0:
0
请输入求解的方程组的维数:m*n
3
7
求解的方程组的维数为3*7维
请输入求解的目标函数的价值系数值:
-3 1 1 0 0 1000 1000
请输入技术系数的值:
1 -2 1 1 0 0 0 -4 1 2 0 -1 1 0 -2 0 1 0 0 0 1
请输入限额系数的值:
11 3 1
请输入基变量的下标值:
3 5 6
结果截屏: