两点之间所有的最短路的算法(Multi-Dijkstra-shortest paths)

摘要

本文主要讲述计算两点之间所有的最短路，有一个误解需要澄清，即两点之间不只有一条最短路！两点之间可能含有多条最短路！

1. 问题引入及介绍

/>

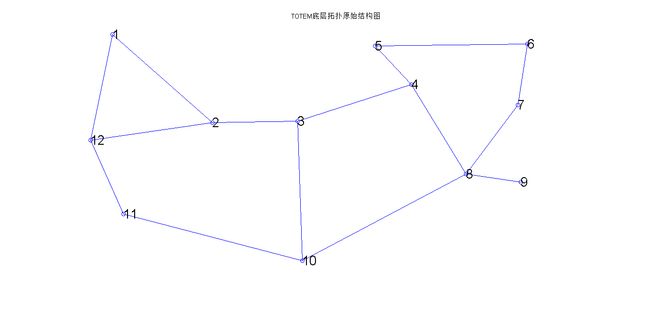
如上图所示，节点对<4, 10>之间的最短路径有两条，一条是：4 -> 3 -> 10；另一条是：4 -> 8 -> 10。这两条最短路的代价值同样都最小。

2. dijkstraSingle.m函数

function [distance,path]=dijkstraSingle(A,s,e)
%% 参数说明
%  邻接矩阵A
%  起点：s
%  终点：e
%  路径长： distance
%  路径：path

%% 算法主体
n=size(A,1);        
D=A(s,:);           
path=[];            
visit=ones(1,n);    
visit(s)=0;        
parent=zeros(1,n);  
for i=1:n-1         
    temp=zeros(1,n);
    count=0;
    for j=1:n
        if visit(j)
            temp=[temp(1:count) D(j)];
        else
            temp=[temp(1:count) inf];
        end
        count=count+1;
    end
    [value,index]=min(temp);
    j=index; visit(j)=0;
    for k=1:n
        if D(k)>D(j)+A(j,k)
            D(k)=D(j)+A(j,k);
            parent(k)=j;
        end
    end
end

%% 结果输出（回溯法）
t = e;  %最短路径  
while t~=s && t>0  
    path =[t,path];  
    p=parent(t);t=p;  
end  
path =[s,path];

if length(path)==1 % 最短路径长度
    distance = A(s,e);
else
    distance=D(e);
end

end  

3. KSP函数

KSP代码详见http://blog.csdn.net/canhui_wang/article/details/51507914

4. 测试

>> dist=[
 Inf     1   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf     1
     1   Inf     1   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf     1
   Inf     1   Inf     1   Inf   Inf   Inf   Inf   Inf     1   Inf   Inf
   Inf   Inf     1   Inf     1   Inf   Inf     1   Inf   Inf   Inf   Inf
   Inf   Inf   Inf     1   Inf     1   Inf   Inf   Inf   Inf   Inf   Inf
   Inf   Inf   Inf   Inf     1   Inf     1   Inf   Inf   Inf   Inf   Inf
   Inf   Inf   Inf   Inf   Inf     1   Inf     1   Inf   Inf   Inf   Inf
   Inf   Inf   Inf     1   Inf   Inf     1   Inf     1     1   Inf   Inf
   Inf   Inf   Inf   Inf   Inf   Inf   Inf     1   Inf   Inf   Inf   Inf
   Inf   Inf     1   Inf   Inf   Inf   Inf     1   Inf   Inf     1   Inf
   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf     1   Inf     1
     1     1   Inf   Inf   Inf   Inf   Inf   Inf   Inf   Inf     1   Inf];

>> [paths, costs]=kShortestPath(dist,4,10,dijkstraSingle(dist,4,10));
>> paths{1}
ans =
     4     3    10
>> costs(1)
ans =
     2
>> paths{2}
ans =
     4     8    10
>> costs(2)
ans =
     2